『深度概念』度量学习中损失函数的学习与深入理解

『深度概念』度量学习中损失函数的学习与深入理解

 

0. 概念简介

 

度量学习（Metric Learning），也称距离度量学习(Distance Metric Learning，DML) 属于机器学习的一种。其本质就是相似度的学习，也可以认为距离学习。因为在一定条件下，相似度和距离可以相互转换。比如在空间坐标的两条向量，既可以用余弦相似度的大小，也可以使用欧式距离的远近来衡量相似程度。

一般的度量学习包含以下步骤：

  1. Encoder编码模型：用于把原始数据编码为特征向量（重点如何训练模型）
  2. 相似度判别算法：将一对特征向量进行相似度比对（重点如何计算相似度，阈值如何设定）

è¿éåå¾çæè¿°​

基于深度学习的度量学习算法中，可以分为两个流派：

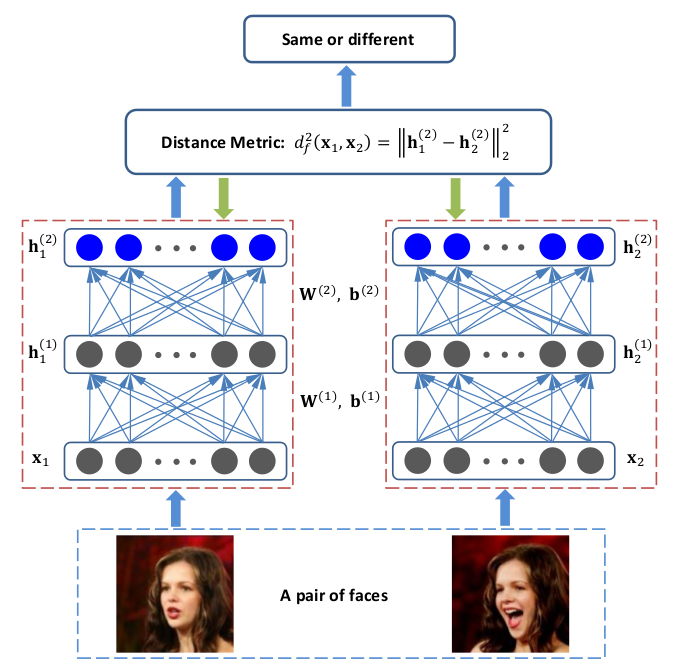
  1. 网络设计派：代表孪生神经网络（Siamese network）
  2. 损失改进派：代表 xx-softmax

本文介绍重点是损失改进派，是最近发展迅速，应用广泛的方法。

在人脸识别与声纹识别这种度量学习算法中，算法的提高主要体现在损失函数的设计上，损失函数会对整个网络的优化有着导向性的作用。可以看到许多常用的损失函数，从传统的softmax loss到cosface, arcface 都有这一定的提高。

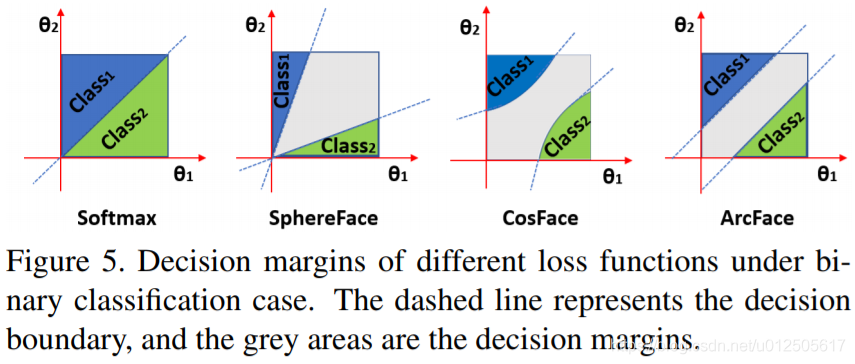
无论是SphereFace、CosineFace还是ArcFace的损失函数，都是基于Softmax loss来进行修改的。

 

Base line Softmax loss
各种延伸的算法 Triplet loss, center loss
最新算法 A-Softmax Loss(SphereFace),  Cosine Margin Loss, Angular Margin Loss, Arcface

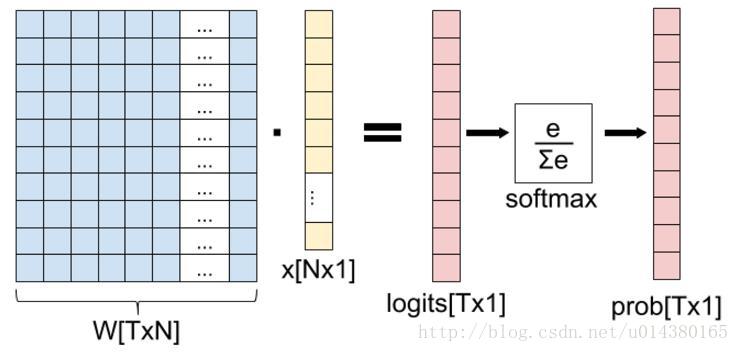
1.Softmax loss

 

    \large L_1 = -\frac{1}{m}{\sum\limits_{i=1}^m}\log\left(\frac{e^{W^T_{y_i}x_i+b_{y_i}}}{ {\sum\limits_{j=1}^n}e^{W^T_jx_i+b_j} }\right)​

 

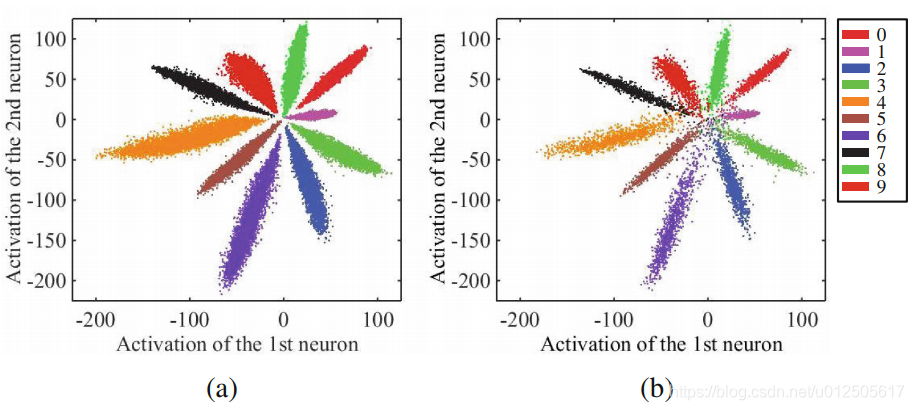
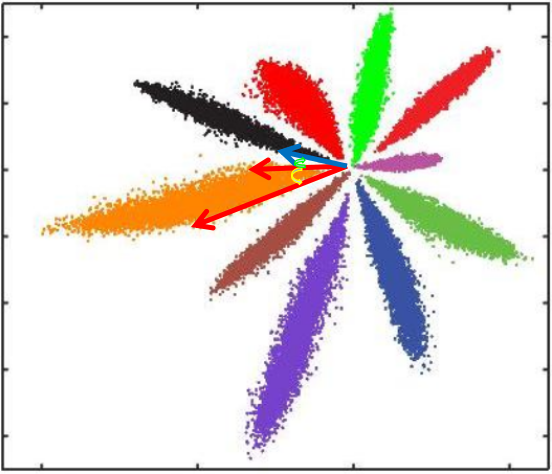
这就是softmax loss函数，{W^T_{j}x_i+b_{j}}​表示全连接层的输出。在计算Loss下降的过程中，我们让{W^T_{j}x_i+b_{j}}​ 的比重变大，从而使得log() 括号内的数更变大来更接近1，就会 log(1) = 0，整个loss就会下降。

其中W和b就是分类层参数，其实就是最后学习到的分类中心，对应下图就是每种颜色对称轴，各种颜色点的集合就是x=encoder（row），就是分类层前面一层的输出。

è¿éåå¾çæè¿°​

下面图如何理解呢？倒数第二层输出不应该是很多维吗？

形象的理解:当做是一个球体，但是为了可视化方便，把球给压扁了。就成为了二维的图像。（个人理解）

如何操作？应该通过降维方法。

这样如何完成分类的？

我们知道，softmax分类时取的是最大那类（argmax），只要目标那一类大于其他类就可以了。反映在图上，每个点与各类中心的距离（W与b决定），距离哪个中心最近就会分成哪一类。

 

​

可以发现，Softmax loss做分类可以很好完成任务，但是如果进行相似度比对就会有比较大的问题

（参加[深度概念]·Softmax优缺点解析）

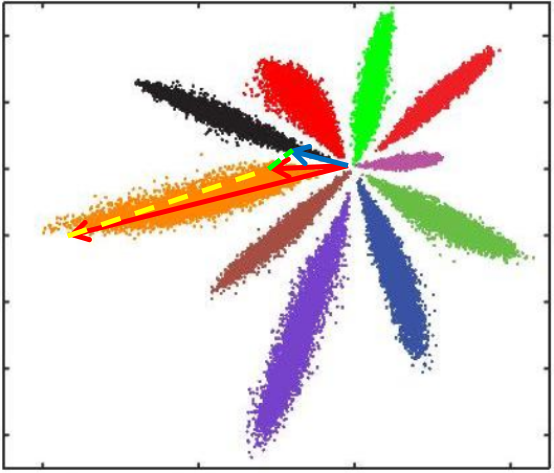
  • L2距离：L2距离越小，向量相似度越高。可能同类的特征向量距离（黄色）比不同类的特征向量距离（绿色）更大

​

  • cos距离：夹角越小，cos距离越大，向量相似度越高。可能同类的特征向量夹角（黄色）比不同类的特征向量夹角（绿色）更大

​

总结来说：

  1. Softmax训练的深度特征，会把整个超空间或者超球，按照分类个数进行划分，保证类别是可分的，这一点对多分类任务如MNIST和ImageNet非常合适，因为测试类别必定在训练类别中。
  2. 但Softmax并不要求类内紧凑和类间分离，这一点非常不适合人脸识别任务，因为训练集的1W人数，相对测试集整个世界70亿人类来说，非常微不足道，而我们不可能拿到所有人的训练样本，更过分的是，一般我们还要求训练集和测试集不重叠。
  3. 所以需要改造Softmax，除了保证可分性外，还要做到特征向量类内尽可能紧凑，类间尽可能分离。

 

这种方式只考虑了能否正确分类，却没有考虑类间距离。所以提出了center loss 损失函数。(paper)

 

2. Center loss

    \large L_C = -\frac{1}{2}{\sum\limits_{i=1}^m}{||x_i-c_{y_i}||}^2​

    \large \Delta{c_j}=\frac{{\sum\limits_{i=1}^m}{\delta{(y_i=j)}\cdot{(c_j-x_i)}}}{1+{\sum\limits_{i=1}^m}{\delta{(y_i=j)}}}​

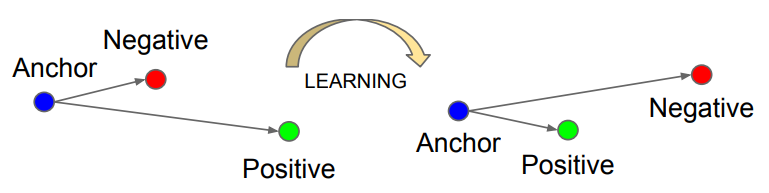
center loss 考虑到不仅仅是分类要对，而且要求类间有一定的距离。上面的公式中\large c_{y_i}​表示某一类的中心，\large x_i​表示每个人脸的特征值。作者在softmax loss的基础上加入了\large L_C​，同时使用参数\large \lambda​来控制类内距离，整体的损失函数如下：

    \large L_2=L_S+L_C= -\frac{1}{m}{\sum\limits_{i=1}^m}\log\left(\frac{e^{W^T_{y_i}x_i+b_{y_i}}}{ {\sum\limits_{j=1}^n}e^{W^T_jx_i+b_j} }\right)+\frac{\lambda}{2}{\sum\limits_{i=1}^m}{||x_i-c_{y_i}||}^2​

​

 

3. Triplet Loss

​

三元组损失函数，三元组由Anchor， Negative， Positive这三个组成。从上图可以看到，一开始Anchor离Positive比较远，我们想让Anchor和Positive尽量的靠近（同类距离），Anchor和Negative尽量的远离（类间距离）。

    \large L_3 = {\sum\limits_{i}^N}{\left [ ||f(x_i^a) - f(x_i^p)||^2_2 - ||f(x_i^a)-f(x_i^n)||_2^2 \right + \alpha ]}​

表达式左边为同类距离 ，右边为不同的类之间的距离。使用梯度下降法优化的过程就是让类内距离不断下降，类间距离不断提升，这样损失函数才能不断地缩小。

上面的几个算法都是比较传统老旧的，下面说一下比较新的算法。

 

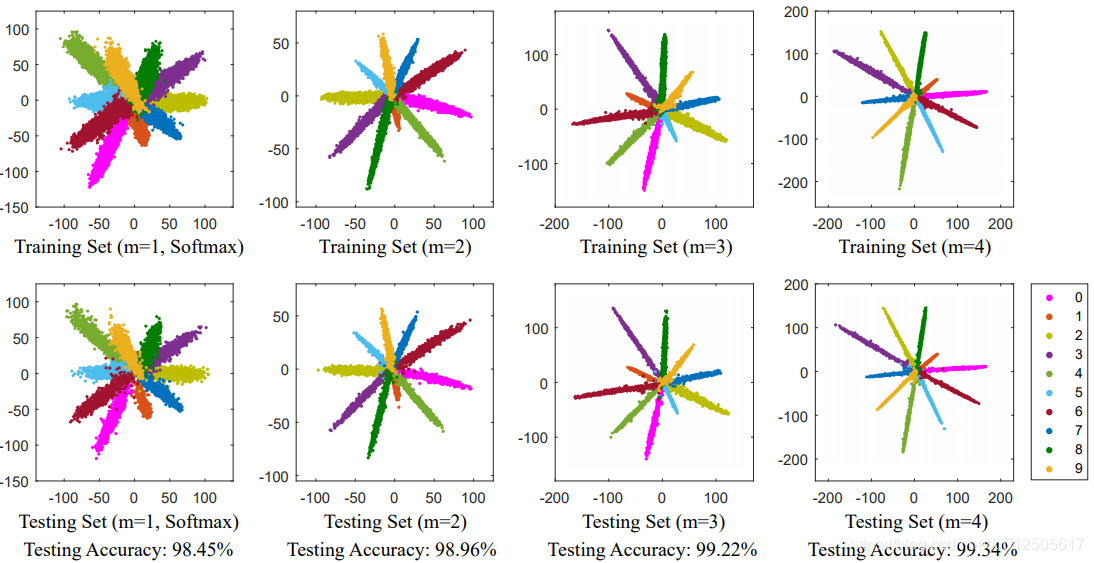
4. L-softmax

前面Softmax loss函数没有考虑类间距离，Center loss函数可以使类内变得紧凑，但没有类间可分，而Triplet loss函数比较耗时，就产生了一下新的算法。

L-softmax函数开始就做了比较精细的改动，从softmax 函数log里面的\large e^{W^T_{y_i}x_i+b_{y_i}​转化到\large e^{||W_{yi}|| ||x_i||\psi{(\theta_{y_i})}}​。L-softmax函数不仅希望类间距离拉的更大，还能够把类内距离压缩的更紧凑。

    \LARGE L_4 = \frac{1}{N}\sum_{i=1}^N L_i = \frac{1}{N}\sum_{i=1}^N -log(\frac{e^{f_y_i}}{\sum_{j}e^{f_i}})​ 

    \LARGE L_i = -log(\frac{e^{||W_{yi}|| ||x_i||\psi{(\theta_{y_i})}}} {e^{||W_{yi}|| ||x_i||\psi{(\theta_{y_i})}} + \sum_{ j\neq y_i}{e^{||W_j|| ||x_i||cos(\theta_j)}}})​

把其中的cosθ改成了cos(mθ)，

    \large \psi(\theta) = \left\{\begin{matrix} \cos (m\theta ), 0\leqslant \theta \leqslant \frac{\pi }{m}& & \\ D(\theta), \frac{\pi}{m}\leqslant \theta \leqslant \pi & & \end{matrix}\right.​

m倍θ起到了增加 margin 的效果，让类内距离更加紧凑，同时类间距离变大。m越大类间距离就越大，因为在(0, π)区间cos函数单调递减，m越大 cos(mθ)趋向于0。

​

 

5. SphereFace(A-Softmax)

A-softmax 是在 L-softmax 函数上做了一个很小的修改，A-softmax 在考虑 margin时添加两个限制条件：将权重W归一化 ||W|| = 1​，b = 0。这使得模型的预测仅取决于 W 和 X 之间的角度。

    \LARGE L_5 = -\frac{1}{N}\sum_{i=1}^{N}log( \frac{e^{||x_i||\cos(m\theta_{y_i})}} {e^{||x_i||\cos(m\theta_{y_i})} + \sum_{j \neq y_i}{e^{||x_i||cos(\theta_j)}}})​

 

6. CosFace

cosface的loss函数如下：

    \LARGE L_6 = -\frac{1}{N} \sum_{i=1}^{N} log( \frac{e^{s(cos(\theta_{yi})-m)}}{e^{s(cos(\theta_{yi})-m)}+ \sum_{j=1, j\neq y_i}^k e^{scos \theta_j}})​

上式中，s为超球面的半径，m为margin。

 

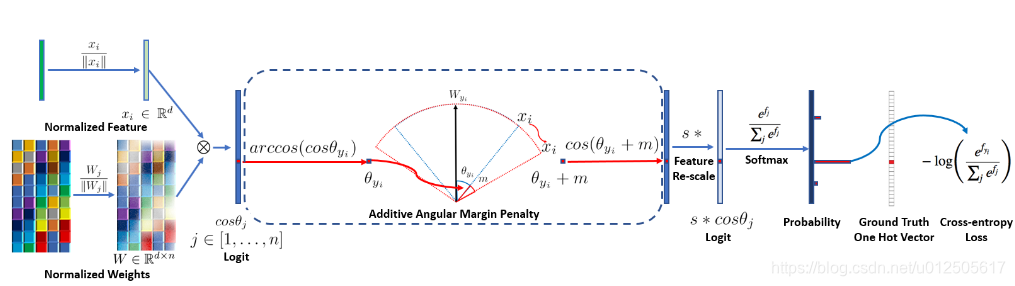
7. ArcFace

对比arcface和cosface这两个函数，发现arcface是直接在角度空间中最大化分类界限，而cosface是在余弦空间中最大化分类界限，这样修改是因为角度距离比余弦距离在对角度的影响更加直接。  

\LARGE L_7= -\frac{1}{N} \sum_{i=1}^{N} log(\frac{e^{s(cos(\theta_{yi}+m))}}{e^{s(cos(\theta_{yi}+m))}+\sum_{j=1,j\neq y_i}^k e^{scos\theta_j}})​

 

分类的决策边界如下：

​

 arcface算法流程如下：

​

 

 

References:

 

[1] https://blog.csdn.net/jningwei/article/details/80641184

[2] https://blog.csdn.net/u012505617/article/details/89355690

 

posted @ 2019-06-20 16:51  小宋是呢  阅读(5508)  评论(0)  编辑  收藏  举报