[深度应用]·Keras极简实现Attention结构
[深度应用]·Keras极简实现Attention结构
在上篇博客中笔者讲解来Attention结构的基本概念，在这篇博客使用Keras搭建一个基于Attention结构网络加深理解。。
1.生成数据
这里让x[:, attention_column] = y[:, 0]，X数据的第一列等于Y数据第零列（其实就是label），这样第一列数据和label的相关度就会很大，最后通过输出相关度来证明思路正确性。
import keras.backend as K
import numpy as np
def get_activations(model, inputs, print_shape_only=False, layer_name=None):
# Documentation is available online on Github at the address below.
# From: https://github.com/philipperemy/keras-visualize-activations
print('----- activations -----')
activations = []
inp = model.input
if layer_name is None:
outputs = [layer.output for layer in model.layers]
else:
outputs = [layer.output for layer in model.layers if layer.name == layer_name] # all layer outputs
funcs = [K.function([inp] + [K.learning_phase()], [out]) for out in outputs] # evaluation functions
layer_outputs = [func([inputs, 1.])[0] for func in funcs]
for layer_activations in layer_outputs:
activations.append(layer_activations)
if print_shape_only:
print(layer_activations.shape)
else:
print(layer_activations)
return activations
def get_data(n, input_dim, attention_column=1):
"""
Data generation. x is purely random except that it's first value equals the target y.
In practice, the network should learn that the target = x[attention_column].
Therefore, most of its attention should be focused on the value addressed by attention_column.
:param n: the number of samples to retrieve.
:param input_dim: the number of dimensions of each element in the series.
:param attention_column: the column linked to the target. Everything else is purely random.
:return: x: model inputs, y: model targets
"""
x = np.random.standard_normal(size=(n, input_dim))
y = np.random.randint(low=0, high=2, size=(n, 1))
x[:, attention_column] = y[:, 0]
return x, y
2.定义网络
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from attention_utils import get_activations, get_data
np.random.seed(1337) # for reproducibility
from keras.models import *
from keras.layers import Input, Dense,Multiply,Activation
input_dim = 4
def Att(att_dim,inputs,name):
V = inputs
QK = Dense(att_dim,bias=None)(inputs)
QK = Activation("softmax",name=name)(QK)
MV = Multiply()([V, QK])
return(MV)
def build_model():
inputs = Input(shape=(input_dim,))
atts1 = Att(input_dim,inputs,"attention_vec")
x = Dense(16)(atts1)
atts2 = Att(16,x,"attention_vec1")
output = Dense(1, activation='sigmoid')(atts2)
model = Model(input=inputs, output=output)
return model3.训练与作图
if __name__ == '__main__':
N = 10000
inputs_1, outputs = get_data(N, input_dim)
print(inputs_1[:2],outputs[:2])
m = build_model()
m.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
print(m.summary())
m.fit(inputs_1, outputs, epochs=20, batch_size=128, validation_split=0.2)
testing_inputs_1, testing_outputs = get_data(1, input_dim)
# Attention vector corresponds to the second matrix.
# The first one is the Inputs output.
attention_vector = get_activations(m, testing_inputs_1,
print_shape_only=True,
layer_name='attention_vec')[0].flatten()
print('attention =', attention_vector)
# plot part.
pd.DataFrame(attention_vector, columns=['attention (%)']).plot(kind='bar',
title='Attention Mechanism as '
'a function of input'
' dimensions.')
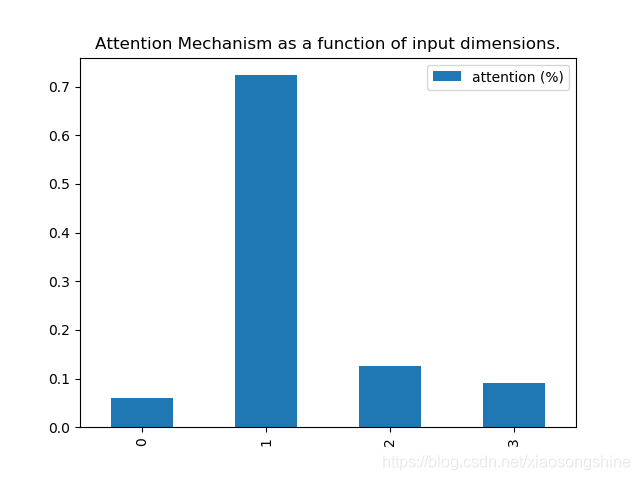
plt.show()4.结果展示
实验结果表明，第一列相关性最大，符合最初的思想。
