《白话统计&&白话统计学》
一、术语
1.1 总体和样本,参数和统计量
- 总体(population):
- 样本:总体的子集
- 参数(parameter):总体数据计算的值,适用于总体
- 统计量(statistic):样本数据计算的值
- 描述统计(descriptive):描述收集数据样本或总体的信息
- 推断统计(inferential):假定收集的样本能够代表更大的总体,利用样本数据得到总体特征的一些结论。
注意:总体可大可小,要看你想研究什么对象;样本不一定能代表总体,假如不能代表总体,此时得到的样本统计量只能用于描述统计,而不能推断总体参数。
1.2抽样
- 随机抽样(random sampling):每一个样本被选中的概率相等。
- 典型抽样(representative sampling):人为的有意选取样本某些特征和总体相匹配。如总体中男女比例7:3,样本选取是男女比例也是7:3。
- 方便抽样(convenience sampling):根据地理位置、接触难度、参与意愿来选择样本。
1.3变量类型和测量尺度
(1)变量类型
- 定量/连续(continuous)变量:身高
- 定性/分类(categorical)变量:男女(二值变量dichotomous variable)
(2)测量尺度 - 定类尺度:又叫分类数据,特点是不可排序不可运算。比如,国籍,不能说中国大于美国。只能对面人口、面积。又比如男女
- 定序尺度:特点是可以排序但不可以运算。比如,健康状况(优良中差),优比良好,但是‘’优‘’减不了‘’良‘’
- 定矩尺度:0点有意义,比如年份1987,零点可以是公元0年,耶稣出生那年。当然0点可以随意定义,假如你统治了时间,你可以把0点定为你出生那年,只要有意义即可。
- 定比尺度:0点无意义,比如体重56公斤,0公斤没有意义。
后两种数据统称为数值数据。可以排序可以运算。
1.4研究设计
- 实验组设计:将样本分成不同组,然后对感兴趣的一个或多个变量进行组间比较。如:AB test
- 相关性研究设计:收集若干变量数据,进行统计分析以确定不同变量之间彼此相关的强度。
实验性设计变量因素可控、可分离,但也很难排除所有的干扰因素。相关性研究设计易于实施,但无法施加精准控制。相关性研究只能提供变量间是否相关的信息(统计理论信息),不能得出实际的因果关系结论(实际业务信息)。
二、分布的集中趋势和分散变异
2.1集中趋势
集中趋势:又称“数据的中心位置”、“集中量数”,一组数据的代表值。是用来描述舆论现象的重要统计分析指标。
(1) 均值(算术平均数)mean
描述平均水平。理论计算方式:

- Outliers(异常值、极端值):数据集中会包含一个或多个数值异常大或异常小的值。异常值检查方法——(四分位计算法)。
- 数据偏斜(skewed data)现象:when the outliers “pull” the data to the left or right。
- Mean最大的缺陷——受outliers影响较大。所以mean最适用的情况为:
The data is symmetric(均匀的)
With the one trend(趋势)均值回归
(2)中位数
定义:将数据按大小顺序(从大到小或是从小到大都可以)排列后处于中间位置的数。 - 理论计算方式——从小到大排序,分为两种情况:
- n=odd number(奇数),median position=(n+1)/2
- n=even number(偶数),median positon=n/2 or n/2+1,so median=two median number/2
- 最适用的情况:the data is skewed by outliers.因为中位数不受outliers影响,只跟序列的位置有关。
(3)四分位数quartile
定义:把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值。 - 下四分位数:Q1,从小到大的顺序排序排在第25%位置的数字。
- 上四分位数:Q3,在第75%位置的数字
- 四分位距interquartile range:IQR,等于Q3-Q1,衡量数据离散程度的一个统计量
- Quartile作用——检查异常值tukey test:
最小值估计=Q1-K * IRQ
最大值估计=Q3+K * IRQ
其中,K=1.5(中度异常)/3(极度异常) - 理论计算方式:
- 方式一,基于n基础
Q1的位置= (n+1) × 0.25
Q2的位置= (n+1) × 0.5
Q3的位置= (n+1) × 0.75 - 方式二,基于n-1基础
Q1的位置=1+(n-1)x 0.25
Q2的位置=1+(n-1)x 0.5
Q3的位置=1+(n-1)x 0.75
如果算出来是小数,取下一个最近的整数。
(4)众数mode——定类数据
-
数据中出现次数最多的数(所占比例最大的数),可能会存在多个众数(多峰),也可能不存在众数。
-
适用的情况:不仅适用于数值型数据,对于非数值型数据也同样适用。
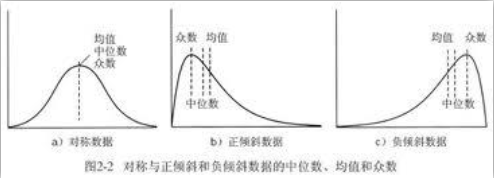
(5)mean、median、mode三者比较

-
Mean>median:数据向右偏(正偏,尾部趋向高端),右端可能存在极大值(右边有大的数据,拉高平均值)
-
Mean<median:数据向左偏(负偏,尾部趋向低端),左端可能存在极小值(左边有小的数据,拉低平均值)
中位数位置不变,均值被拉向尾巴一端。比如最大的数为100时,中位数和均值相等,变成200后(正偏),均值被拉大,中位数不变。
(6) 异常值检查方法
异常值检查方法
2.2 离散程度和相关性
对于离散程度的程度衡量,可以只针对单一变量自身离散程度,如极差、方差、标准差、变异系数等;也可以针对多变量的离散程度之间的相关性,如协方差、相关系数、皮尔森系数。
-
极差range:max()-min()
-
四分位差interquartile range:75%-25%(分成四组,包含中间两组数)
-
离差deviation:点到均值之差。与原单位相同
-
离差平方和:离差的平方后求和相加。消除正负抵消,相加为0。单位:原单位的平方。平方和基础统计学的重要组成部分。
-
方差variance:点到均值的距离平方(离差平方)和的平均,单位:原单位的平方。一般不用来描述分布,用来作为计算其他统计量(如方差分析)的一个步骤,而不是单独使用的统计量。
-
标准差stardard deviation:方差开方,单位:和原单位相同。更喜欢用标准差描述一个分布中取值的平均离散程度。结合均值可以很好描述一个分布的形态。

- 变异系数(coefficient of variation):
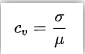
变异系数CV,又称“离散系数”(英文:coefficient of variation),是概率分布离散程度的一个归一化量度,其定义为标准差与平均值之比。单位:无量纲。
- 协方差:
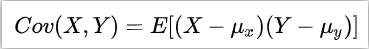
假若有两个变量X,Y,每个时刻的“X值与其均值只差”乘以“Y值与其均值之差”得到一个乘积,再对这每时刻的乘积求和并求出均值。
反映两个变量在变化过程中,是同向变化还是反向变化,同向或反向的程度如何:
- 你变大,我也变大,说明两变量是同向变化,协方差为正;
- 你变大,同时我变小,说明两变量是反向变化,协方差为负;
- 协方差数值越大,两变量同向程度也越大,反之亦然。
- 相关系数:
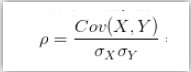
用X、Y的协方差除以X的标准差和Y的标准差。相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。
也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负;
由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。 - 皮尔森系数(pearson):
参考网站:
协方差和相关系数史诗级白话介绍:协方差和相关系数
三、分布
3.1 累计函数和概率密度函数
参考网站:累计函数和概率密度函数
①离散型数据
概率函数(概率分布、分布律):离散随机变量X取不同的值,对应不同的概率值。
概率分布函数(累计概率函数)F(x):概率函数取值的累加结果。

②连续型数据
概率密度函数(连续型数据概率函数)f(x):连续型数据,某点的概率为0。只能用某点数据密集程度表示概率分布情况。

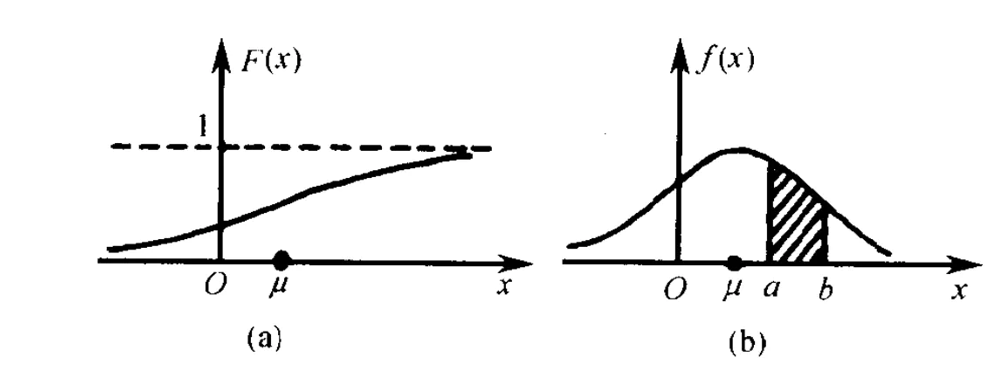
左边是F(x)连续型随机变量分布函数画出的图形,右边是f(x)连续型随机变量的概率密度函数画出的图像,它们之间的关系就是,概率密度函数是分布函数的导函数。
3.4 正态分布(Normal Distribution)
(1)正态分布描述现象
普通分布,描述某些稳定但又受到一些偶然因素影响的现象。
(2)正态分布概率密度函数
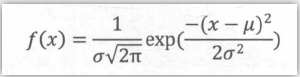
(3)正态分布密度函数数学意义
- f(x)永远大于0,左右对称,当x=μ,即等于均数时,概率密度函数达到最大值;
- x离均数越远,f(x)值越小,距离无限远时,趋于0;
- 标准差σ越大,f(x)值越小,分布形状越“矮”,峰度平坦;反之,越’瘦高‘。
- 中位数=均值=众数
正态分布由两个参数决定:均数和标准差。均数是位置参数,决定分布集中的位置;标准差是形状参数,决定分布的分散程度。
(4)正态分布统计规律
- 1倍标准差面积:68.2%
- 1.96倍标准差:95%
- 2倍标准差:95.4%
- 3倍标准差:99.7%,1000大概会有3次错误发生的概率。
- 6倍标准差:之外的面积为百万分之2。100万份样品出现2次错误。
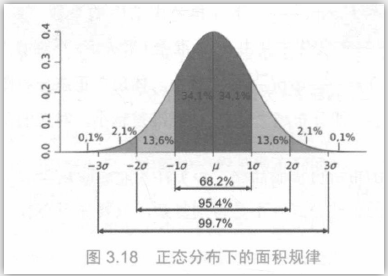
比如,X变量(身高)服从:X~N(μ,σ2),其中μ=170,σ=10,则95%的人身高值都落在[150.4,189.6]之间。
假若是有偏分布,再用正态分布的统计规律去估算概率,就会变得不准确。比如,正偏分布(多数取值位于较小一端,少数取值位于较大一端),从正态分布得出的概率将低估较小一端的实际取值个数,高估较大一端实际取值个数。
(5)小概率事件(P<0.05)
P<0.05,认为差异有统计学意义。对于正态分布来说,两侧面积小于5%。即均数往左往右各1.96倍标准差时,对应的左侧和右侧面积之和就是5%。这个概率很低,一般情况不会发生,认为是小概率事件。
(6)标准正态分布——Z分数(Z变换)(Standarized Normal Distribution)
为什么要进行Z变换?——消除不同测量单位的差异,类似于方差和标准差思想。
例子:
生物100分,考了65分;统计学200分,考了42分。哪门成绩更好?假如“更好”意味着答题正确率,显然生物更好。但是这不公平,因为题目难度不一样,统计学比生物难太多。公平的做法是,与全班同学相比,成绩处于哪个百分点。
生物:μ=60,σ=10,意味着分数比均值高5分(0.5个标准差);
统计:μ=37,σ=5 ,意味着分数比均值高5分(1.0个标准差);
3.5 几个常见分布:t分布、x2分布,F分布
T检验对应t分布,x2检验对应x2分布,方差分析对应F分布。
(1)T分布
(2)x2分布
(3)F分布
四、数据资料分类
五、描述统计
六、中心极限定理和大数定理
七、假设检验
7.2 零假设和备择假设
零假设(无效假设Null Hypothesis):一般从正面做出假设(不具备XXX,没有XXX等)。
八、参数估计
九、置信区间
十、统计方法串讲
10.1 一般线性模型(General Linear Model)——方差分析与线性回归统计
①t检验、方差分析、线性回归用途
- t检验——两组均值比较
- 方差分析——多组均值比较
- 线性回归——自变量对因变量的影响分析
②一般线性模型
t检验、方差分析、线性回归等都属于一般线性模型,一般线性模型基本形式:
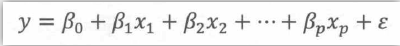
y:因变量(反应变量、结局变量),x:自变量(解释变量、预测变量)。β0表示截距,反映自变量x=0时,y的均值。β1、β2表示斜率,反映自变量增加1单位,y值变动的大小。
一般线性模型中,因变量必须是定量的(连续),自变量可以是定量或分类。自变量的不同形式对应不同的统计方法:

十一、正态性和方差齐性
①做正态性检验必要性
保证样本数据的随机性,因为随机数就是正态分布的。
②正态性和方差齐性含义
正态性和方差性是经典统计模型应用的两个前提条件,t检验、方差分析、线性回归等都需要满足这两个条件:
- 正态性(Normality):严格上说是残差要符合正态分布,不过实际中都是对因变量进行正态性检验。
- 方差齐性(Equality of Variances):即方差相等,自变量x每取一个值,因变量(严格说是残差)的方差基本相等。
11.1 用统计检验方法判断正态性
(1)基于峰度和偏度的SW(Shapiro-Wilk)检验
①峰度和偏度
- 峰度(Kurtosis):分布形状是平坦还是尖峰,上下维度。
- 偏度(Skewness):分布形状是否对称,左右维度。
②正态分布的峰度和偏度
正态分布的峰度和偏度均为0。峰度>0,尖峰;峰度<0,平坦峰。偏度>0,右偏态(正偏);偏度<0,左偏态(负偏)。
(2)基于拟合优度KS、CVM、AD检验
KS(Kolmogorov-Smirnov)、CVM(Cramer-von Mises)、AD(Anderson-Darling)
①拟合优度思想
基于理论分布与基于实际数据得到的分布之间的差异。这种思想不仅可以用于正态分布,还可以用于其他分布检验。
②正态分布拟合优度检验思路
先求出正态分布的累积分布函数(CDF,Cumulative Distribution Function)——>样本数据与该函数差别——>差别不大,接近正态分布——>差别较大,样本数据可能不服从正态分布。
③三种方法对“差别”的定义
三种检验都基于此思想,区别在于对“差别”定义:
- KS:取绝对值
- CVM:取平方
- AD:对CVM的改进
④参考网站
KS:KS
python正态检验方法:python正态检验方法
11.2 用描述的方法判断正态性——图形判断
(1)Q-Q图和P-P图
①Q-Q图含义和检验原理
Q-Q(Quantile-Quantile),分位数-分位数图。横坐标,理论正态分位数,纵坐标,实际数据分位数。
比较分位数和实际分位数差别。无差别,点集中在一条直线,正态分布。有差别,偏离直线较远。
②P-P图
P-P(Probability-Probability),和Q-Q类似,用的是累计概率。
(2)茎叶图
(3)用四分位数间距和标准差进行简易判断
正态分布四分位间距(IQR)和标准差(s)之比大约为1.34。若IQR/s=1.34左右,基本满足正态分布。
11.3 方差分析中方差齐性判断
①方差齐性判断
就是判断两组或多组的方差是否相等,样本抽样是不是随机的。方差不等会严重影响方差分析的F检验。
②各种检验方法
...................................



