平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树
平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树
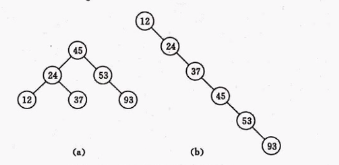
(a)和(b)都是排序二叉树,但是查找(b)的93节点就需要查找6次,查找(a)的93节点就需要查找3次,所以(b)的效率不高。
平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树的深度只差的绝对值不超过1。若将二叉树上节点的平衡因子BF(Balance Factor)定义为该节点的左子树的深度减去它右子树的深度,则平衡二叉树上所有节点的平衡因子只可能是-1,0,1。只要二叉树上有一个节点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。
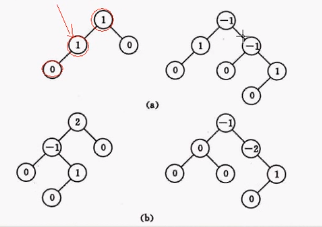
上图(a)是平衡二叉树,(b)不是平衡二叉树,因为有的节点的平衡因子大于1了。
插入节点的大致思路:
- 首先找到插入节点的位置,插入节点
- 插入节点后,调整相关节点的平衡因子
- 调整平衡因子后,如果发现树不平衡了,就要进行节点的调整(单左旋转,或单右旋转,或双旋转(先左后又,或者先右后左)。
avl_tree.h
#ifndef __AVLTREE__
#define __AVLTREE__
#include<stdio.h>
#include<malloc.h>
#include<assert.h>
#include "nodestack.h"
#define Type int
#define FALSE 0
#define TRUE 1
#define BOOL int
typedef struct AVLNode{
Type data;
struct AVLNode* left;
struct AVLNode* right;
int bf;//平衡因子
}AVLNode;
typedef struct AVLTree{
struct AVLNode* root;
}AVLTree;
void init_avl_tree(AVLTree* avl);
//插入节点
BOOL insert_avl(AVLTree* avl, Type t);
#endif
avl_tree.c
#include "avl_tree.h"
void init_avl_tree(AVLTree* avl){
avl->root = NULL;
}
AVLNode* malNode(Type x){
AVLNode* t = (AVLNode*)malloc(sizeof(AVLNode));
assert(NULL != t);
t->data = x;
t->left = NULL;
t->right = NULL;
t->bf = 0;
return t;
}
//右旋转
void rotateR(AVLNode** t){
AVLNode* subR = *t;
*t = (*t)->left;
subR->left = (*t)->right;
(*t)->right = subR;
(*t)->bf = 0;
subR->bf = 0;
}
//左旋转
void rotateL(AVLNode** t){
AVLNode* subL = *t;
*t = (*t)->right;
subL->right = (*t)->left;
(*t)->left = subL;
(*t)->bf = 0;
subL->bf = 0;
}
//左右旋转
void rotateLR(AVLNode** t){
AVLNode* subR = *t;
AVLNode* subL = subR->left;
*t = subL->right;
subL->right = (*t)->left;
(*t)->left = subL;
if((*t)->bf <= 0){///??
subL->bf = 0;
}
else{
subL->bf = -1;
}
subR->left = (*t)->right;
(*t)->right = subR;
if((*t)->bf == -1){
subR->bf = 1;//???
}
else{
subR->bf = 0;//???
}
(*t)->bf = 0;
}
//右左旋转
void rotateRL(AVLNode** t){
AVLNode* subL = *t;
AVLNode* subR = subL->right;
*t = subR->left;
subR->left = (*t)->right;
(*t)->right = subR;
if((*t)->bf >= 0){
subR->bf = 0;
}
else{
subR->bf = 1;
}
subL->right = (*t)->left;
(*t)->left = subL;
if((*t)->bf == 1){
subL->bf = -1;
}
else{
subL->bf = 0;
}
(*t)->bf = 0;
}
//插入树的节点
BOOL insert_avl_node(AVLNode** t, Type x){
AVLNode* p = *t;
AVLNode* parent = NULL;
nodestack st;
init(&st);
while(p != NULL){
if(x == p->data)
return FALSE;
parent = p;
push(&st, parent);
if(x < p->data)
p = p->left;
else
p = p->right;
}
p = malNode(x);
//插入节点为root节点
if(parent == NULL){
*t = p;
return TRUE;
}
//插入节点不是root节点
if(x < parent->data)
parent->left = p;
else
parent->right = p;
//调整BF
while(length(&st) != 0){
parent = getTop(&st);
pop(&st);
if(parent->left == p){
parent->bf--;
}
else{
parent->bf++;
}
if(parent->bf == 0){
break;
}
if(parent->bf == 1 || parent->bf == -1){
p = parent;
}
else{
//旋转树,让树变成平衡树
int flag = (parent->bf < 0) ? -1 : 1;
//符号相同,说明是一条直线,不是折线,所以单旋转
if(p->bf == flag){
//因为是撇/,所以右旋转
if(flag == -1){
rotateR(&parent);
}
//因为是捺\,所以左旋转
else{
rotateL(&parent);
}
}
//符号不同,说明是折线,所以双旋转
else{
//折线的角指向右>
if(flag == 1){
rotateRL(&parent);
}
//折线的角指向左<
else{
rotateLR(&parent);
}
}
break;
}
}
if(length(&st) == 0){
*t = parent;
}
else{
AVLNode* q = getTop(&st);
if(q->data > parent->data){
q->left = parent;
}
else{
q->right = parent;
}
}
clear(&st);
return TRUE;
}
//插入节点
BOOL insert_avl(AVLTree* avl, Type t){
return insert_avl_node(&avl->root, t);
}
avl_treemain.c
#include "avl_tree.h"
int main(){
AVLTree avl;
init_avl_tree(&avl);
//Type ar[] = {13,24,37,90,53};
//Type ar[] = {30,20,10};
//Type ar[] = {30,20,40,10,25,5,22,28,21};
//Type ar[] = {30,20,10};
//Type ar[] = {50,40,60,10,45,70,5,30,20,12};
Type ar[] = {30,20,50,10,40,70,60,80,55};
int n = sizeof(ar) / sizeof(Type);
for(int i = 0; i < n; ++i){
insert_avl(&avl, ar[i]);
}
return 0;
}
编译方法:g++ -g nodestack.c avl_tree.c avl_treemain.c




 浙公网安备 33010602011771号
浙公网安备 33010602011771号