c/c++ 二叉排序树
c/c++ 二叉排序树
概念:
左树的所有节点的值(包括子节点)必须小于中心节点,右树所有节点的值(包括子节点)必须大于中心节点。
不允许有值相同的节点。
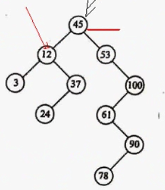
二叉排序树的特点:
- 中序遍历后,就是从小到大排序了。
- 根节点的最左边的值,就是树中最小的值。
- 根节点的最右边的值,就是树中最大的值。
创建二叉排序树的思路:
- 用递归的方式
- 和根节点比较大小
- 比根节点小的话,用递归去和根节点的左节点比较,至到找到合适的位置
- 比根节点大的话,用递归去和根节点的右节点比较,至到找到合适的位置
二叉排序树的一些实用函数
| init_bst | 初始化二叉排序树 |
|---|---|
| insert_bst_tree | 插入树的节点 |
| min | 求树中最小节点 |
| max | 求树中最大节点 |
| sort | 排序二叉树(中序遍历就是从小到大排序了) |
| remove_bst | 删除节点 |
删除节点
pattern1:要被删除的节点是root节点
- 方案1:用根节点左树中的最大的节点作为新的根节点
删除45

- 方案2:用根节点又树中的最小的节点作为新的根节点
删除45
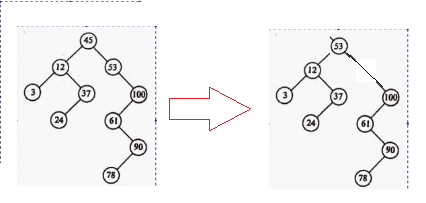
pattern2:要被删除的节点是其父节点的左树,并且要被删除的节点有右树
删除12
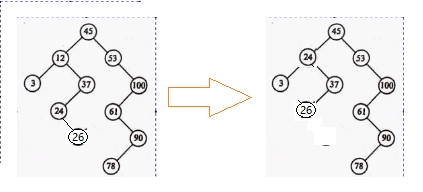
pattern3:要被删除的节点是其父节点的左树,并且要被删除的节点无右树
删除12

pattern4:要被删除的节点是其父节点的右树,并且要被删除的节点无左树
删除53

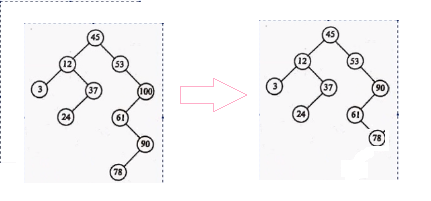
pattern5:要被删除的节点是其父节点的右树,并且要被删除的节点有左树
删除100
bst.h
#ifndef __BST__
#define __BST__
#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#define T int
#define FALSE 0
#define TRUE 1
#define BOOL int
typedef struct BSTNode{
T data;
struct BSTNode* left;
struct BSTNode* right;
}BSTNode;
typedef struct BST{
BSTNode* root;
}BST;
//初始化二叉排序树
void init_bst(BST* bst);
//插入树的节点
BOOL insert_bst_node(BSTNode** t, T x);
BOOL insert_bst_tree(BST* bst, T x);
//求树中最小节点
T min(BST* bst);
//求树中最大节点
T max(BST* bst);
//排序
void sort(BST* bst);
//查找父节点
BSTNode* get_parent(BST* bst, BSTNode* tar);
//删除节点
BOOL remove_bst(BST* bst, T key);
//搜索节点
BSTNode* search_bst(BST* bst, T key);
//搜索节点
BSTNode* search_bst1(BST* bst, T key);
//清空树
void clear_bst(BST* bst);
#endif
bst.c
#include "bst.h"
//初始化二叉排序树
void init_bst(BST* bst){
bst->root = NULL;
}
//插入树的节点
BOOL insert_bst_node(BSTNode** t, T x){
if(*t == NULL){
*t = (BSTNode*)malloc(sizeof(BSTNode));
assert(NULL != *t);
(*t)->data = x;
(*t)->left = NULL;
(*t)->right = NULL;
return TRUE;
}
else if(x < (*t)->data){
insert_bst_node(&((*t)->left), x);
}
else if(x > (*t)->data){
insert_bst_node(&((*t)->right), x);
}
return FALSE;
}
BOOL insert_bst_tree(BST* bst, T x){
return insert_bst_node(&(bst->root), x);
}
//求树中最小节点
T min_node(BSTNode* t){
while(t->left != NULL)
t = t->left;
return t->data;
}
T min(BST* bst){
assert(bst->root != NULL);
return min_node(bst->root);
}
//求树中最大节点
T max_node(BSTNode* t){
while(t->right != NULL){
t = t->right;
}
return t->data;
}
T max(BST* bst){
assert(bst->root != NULL);
return max_node(bst->root);
}
//二叉树中序排序
void sort_node(BSTNode* t){
if(NULL == t){
return;
}else{
sort_node(t->left);
printf("%d ", t->data);
sort_node(t->right);
}
}
void sort(BST* bst){
assert(NULL != bst->root);
sort_node(bst->root);
}
//搜索节点
BSTNode* search_node(BSTNode* t, T key){
if(NULL == t || t->data == key){
return t;
}
else{
BSTNode* p;
p = search_node(t->left, key);
if(NULL == p){
p = search_node(t->right, key);
}
return p;
}
}
BSTNode* search_bst(BST* bst, T key){
return search_node(bst->root, key);
}
BSTNode* search_node1(BSTNode* t, T key){
if(NULL == t || t->data == key){
return t;
}
else{
if(key < t->data){
search_node1(t->left, key);
}
else{
search_node1(t->right, key);
}
}
}
BSTNode* search_bst1(BST* bst, T key){
return search_node1(bst->root, key);
}
//清空树
void clear_node(BSTNode** t){
if(NULL != *t){
clear_node(&((*t)->left));
clear_node(&((*t)->right));
free(*t);
*t = NULL;
}
}
void clear_bst(BST* bst){
clear_node(&bst->root);
}
//查找父节点
BSTNode* get_parent_node(BSTNode* t, BSTNode* tar){
if(NULL == t || NULL == tar)return NULL;
if(t->left == tar || t->right == tar){
return t;
}
else{
BSTNode* p = NULL;
p = get_parent_node(t->left, tar);
if(NULL == p){
p = get_parent_node(t->right, tar);
}
return p;
}
}
BSTNode* get_parent(BST* bst, BSTNode* tar){
return get_parent_node(bst->root, tar);
}
BOOL remove_bst(BST* bst, T key){
BSTNode* tar = search_bst(bst, key);
//树为空或者要删除的节点不存在,返回失败
if(bst->root == NULL || NULL == tar) return FALSE;
BSTNode* parent = get_parent(bst, tar);
//因为要被删除的顶点有左子节点,所以要找到以左子节点为根的右子节点中值最大的
BSTNode* X = NULL;
if(NULL != tar->left){
X = tar->left;
while(X->right != NULL){
X = X->right;
}
//因为要被删除的顶点的左子节点,有右子节点,所以要找到最大的
if(X != tar->left){
//找到最大节点的父节点
BSTNode* X1 = get_parent(bst, X);
//最大节点的父节点的右边指向最大节点的左边
X1->right = X->left;
//最大节点的左边代替被删除节点的左边,右边代替右边
X->left = tar->left;
X->right = tar->right;
}
//因为要被删除的顶点的左子节点,没有右子节点,所以它就是最大的
else{
X->right = tar->right;
}
}
//因为要被删除的顶点没有左子节点,所以要找到以右子节点为根的左子节点中值最小的
else{
X = tar->right;
//要被删除的节点既没有左节点,也没有右节点
if(NULL == X){
//找到父节点
BSTNode* X2 = get_parent(bst, X);
//要被删除的节点不是根节点
if(parent != NULL){
//要被删除的顶点在父节点的左边
if(tar->data < parent->data){
parent->left = X;
}
//要被删除的顶点在父节点的右边
else{
parent->right = X;
}
}
else{
bst->root = NULL;
}
free(tar);
return TRUE;
}
while(X->left != NULL){
X = X->left;
}
//因为要被删除的顶点的右子节点,有左子节点,所以要找到最小的
if(X != tar->right){
//找到最小节点的父节点
BSTNode* X1 = get_parent(bst, X);
//最小节点的父节点的左边指向最小节点的右边
X1->left = X->right;
//最小节点的左边代替被删除节点的左边,右边代替右边
X->right = tar->right;
X->left = tar->left;
}
}
//要被删除的节点不是根节点
if(parent != NULL){
//要被删除的顶点在父节点的左边
if(tar->data < parent->data){
parent->left = X;
}
//要被删除的顶点在父节点的右边
else{
parent->right = X;
}
}
else{
bst->root = X;
}
free(tar);
}
bstmain.c
#include "bst.h"
int main(){
BST bst;
init_bst(&bst);
//patten1 目标节点是root,root没有右子节点,左子节点中有右子节点
//T ar[] = {45,12,3,37,24,38};
//patten2 目标节点是root,root没有右子节点,左子节点中没有右子节点
//T ar[] = {45,12,3};
//patten3 目标节点是root,只有root节点
//T ar[] = {45};
//patten4 目标节点是root,root有右子节点,右子节点中没有左子节点
//T ar[] = {45,12,53,3,37,100,24};
//patten5 目标节点是root,root有右子节点,右子节点中有左子节点
//T ar[] = {45,12,53,3,37,100,24,61,90,78};
//patten6 目标节点(8)不是root,目标节点有左子节点,左子节点没有右边
//T ar[] = {45,12,53,3,27,2,4,24,1,6,5,8,7};
//patten7 目标节点(12)不是root,目标节点有左子节点,左子节点有右边
//T ar[] = {45,12,53,3,27,2,4,24,1,6,5,8,7};
//patten8 目标节点(120)不是root,目标节点没有左子节点,右子节点没有左边
T ar[] = {45,12,53,3,37,52,100,2,4,24,51,61,120,1,6,90,130,5,8,78,126,140,7,124,127,125};
//T ar[] = {45,12,53,3,37,100,24,61,90,78};
//T ar[] = {45,3,4,12,53};
int n = sizeof(ar) / sizeof(T);
for(int i = 0; i < n; ++i){
insert_bst_tree(&bst, ar[i]);
}
sort(&bst);
printf("\n");
//删除节点
remove_bst(&bst, 45);
sort(&bst);
printf("\n");
clear_bst(&bst);
}
编译方法:gcc -g bst.c bstmain.c




 浙公网安备 33010602011771号
浙公网安备 33010602011771号