c/c++求解图的关键路径 critical path
c/c++求解图的关键路径 critical path

上图表示一个工程,工程以V1为起始子工程,V9为终止子工程。
由图可以看出,要开工V5工程,必须在完成工程V2和V3后才可以。
完成V2需要a1(6)个小时,完成V3需要a2(4)个小时。假设V2和V3同时开工,V3就会提前2个小时完工,但是这时V2还没有完工,所以V5还不能开始。所以为了要开工V5必须V2要完成,V3即使晚开工2个小时,也不会耽误V5的开工,所以V2就是V5的 关键路径(Critical Path)。
有2个问题:(1)完成整个工程至少需要多少时间。(2)哪些子工程是影响总工程进度的关键?
(1)的答案:关键路径上的时间总和是完成整个工程至少需要的时间。
(2)的答案:关键路径上的工程是影响总工程进度的关键。
查找关键路径的目的:
辨别哪些是关键工程,以便争取提高关键工程的效率,缩短整个工期。
从上图可以得知,工程V6延迟3天开工,或者延迟3个完成都不会影响项目的工期,所以V6不在关键路径上。
实现思路:
-
假设e(i)表示活动a(i)的最早开始时间,在不推迟整个工程完成的前提下,用l(i)表示活动a(i)的最迟开始时间。两者之差表示完成活动a(i)的时间余量。余量为0的活动就是关键活动,所以连接此活动的2个顶点就是关键路径上的顶点。可以看出,即使提前完成非关键活动,也不能加快工程的进度。
-
辨别关键活动就是要找到e(i) = l(i)的活动。为了求得活动的e(i)和l(i),首先应求得事件(顶点)的最早发生时间ve(i)和最迟发生时间vl(i)。如果活动a(i),由边<j, k>表示,其持续时间记为dut(<j, k>),则有如下公式:
e(i) = ve(i)
l(i) = vl(k) - dut(<j, k>)
-
ve的求法用拓扑排序
-
vl的求法用逆拓扑排序
求下图的关键路径
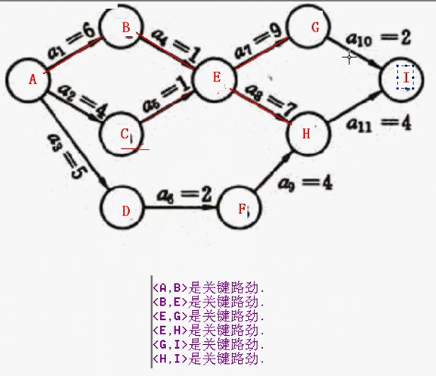
critical_path.h
#ifndef __criticalpath__
#define __criticalpath__
#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#include <memory.h>
#define Default_vertex_size 10
#define T char//dai biao ding dian de lei xing
#define E int
#define MAX_COST 0x7FFFFFFF
typedef struct GraphMtx{
int MaxVertices;//zui da ding dian shu liang]
int NumVertices;//shi ji ding dian shu liang
int NumEdges;//bian de shu lian
T* VerticesList;//ding dian list
int** Edge;//bian de lian jie xin xi, bu shi 0 jiu shi 1
}GraphMtx;
//chu shi hua tu
void init_graph(GraphMtx* gm);
//打印二维数组
void show_graph(GraphMtx* gm);
//插入顶点
void insert_vertex(GraphMtx* gm, T v);
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost);
//取得与v顶点有连线的第一个顶点
int getNeighbor(GraphMtx* gm, T v);
//取得与v1顶点,v1顶点之后的v2顶点的之后的有连线的第一个顶点
int getNextNeighbor(GraphMtx* gm, T v1, T v2);
E getWeight(GraphMtx* g, int v1, int v2);
//求解关键路径
void critical_path(GraphMtx* g);
#endif
critical_path.c
#include "critical_path.h"
void init_graph(GraphMtx* gm){
gm->MaxVertices = Default_vertex_size;
gm->NumEdges = gm->NumVertices = 0;
//kai pi ding dian de nei cun kong jian
gm->VerticesList = (T*)malloc(sizeof(T) * (gm->MaxVertices));
assert(NULL != gm->VerticesList);
//创建二维数组
//让一个int的二级指针,指向一个有8个int一级指针的数组
//开辟一个能存放gm->MaxVertices个int一级指针的内存空间
gm->Edge = (int**)malloc(sizeof(int*) * (gm->MaxVertices));
assert(NULL != gm->Edge);
//开辟gm->MaxVertices组,能存放gm->MaxVertices个int的内存空间
for(int i = 0; i < gm->MaxVertices; ++i){
gm->Edge[i] = (int*)malloc(sizeof(int) * gm->MaxVertices);
}
//初始化二维数组
//让每个顶点之间的边的关系都为不相连的
for(int i = 0; i < gm->MaxVertices; ++i){
for(int j = 0; j < gm->MaxVertices; ++j){
gm->Edge[i][j] = 0;
}
}
}
//打印二维数组
void show_graph(GraphMtx* gm){
printf(" ");
for(int i = 0; i < gm->NumVertices; ++i){
printf("%c ", gm->VerticesList[i]);
}
printf("\n");
for(int i = 0; i < gm->NumVertices; ++i){
//在行首,打印出顶点的名字
printf("%c:", gm->VerticesList[i]);
for(int j = 0; j < gm->NumVertices; ++j){
printf("%d ", gm->Edge[i][j]);
}
printf("\n");
}
printf("\n");
}
//插入顶点
void insert_vertex(GraphMtx* gm, T v){
//顶点空间已满,不能再插入顶点了
if(gm->NumVertices >= gm->MaxVertices){
return;
}
gm->VerticesList[gm->NumVertices++] = v;
}
int getVertexIndex(GraphMtx* gm, T v){
for(int i = 0; i < gm->NumVertices; ++i){
if(gm->VerticesList[i] == v)return i;
}
return -1;
}
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost){
if(v1 == v2)return;
//查找2个顶点的下标
int j = getVertexIndex(gm, v1);
int k = getVertexIndex(gm, v2);
//说明找到顶点了,并且点之间还没有线
if(j != -1 && k != -1 && gm->Edge[j][k] != 1){
//因为是有方向,所以更新1个值
gm->Edge[j][k] = cost;
//边数加一
gm->NumEdges++;
}
}
//取得与某顶点有连线的第一个顶点
int getNeighbor(GraphMtx* gm, T v){
int p = getVertexIndex(gm, v);
if(-1 == p)return -1;
for(int i = 0; i < gm->NumVertices; ++i){
if(gm->Edge[p][i] != 0)
return i;
}
return -1;
}
//取得与v1顶点,v1顶点之后的v2顶点的之后的有连线的第一个顶点
int getNextNeighbor(GraphMtx* gm, T v1, T v2){
if(v1 == v2)return -1;
int p1 = getVertexIndex(gm, v1);
int p2 = getVertexIndex(gm, v2);
if(p1 == -1 || p2 == -1)return -1;
for(int i = p2 + 1; i < gm->NumVertices; ++i){
if(gm->Edge[p1][i] != 0)
return i;
}
return -1;
}
E getWeight(GraphMtx* g, int v1, int v2){
if(v1 == -1 || v2 == -1)return 0;
return g->Edge[v1][v2];
}
//求解关键路径
void critical_path(GraphMtx* g){
int n = g->NumVertices;
//最早开始时间数组
int* ve = (int*)malloc(sizeof(int) * n);
//最晚开始时间数组
int* vl = (int*)malloc(sizeof(int) * n);
assert(NULL != ve && NULL != vl);
for(int i = 0; i < n; ++i){
ve[i] = 0;
vl[i] = MAX_COST;
}
int j, w;
//ve
for(int i = 0; i < n; ++i){
j = getNeighbor(g, g->VerticesList[i]);
while(j != -1){
w = getWeight(g, i, j);
if(ve[i] + w > ve[j]){
ve[j] = ve[i] + w;
}
j = getNextNeighbor(g,g->VerticesList[i],g->VerticesList[j]);
}
}
//ve 的结果看下图a
//vl
vl[n-1] = ve[n-1];
for(int i = n - 2; i > 0; --i){
j = getNeighbor(g, g->VerticesList[i]);
while(j != -1){
w = getWeight(g, i, j);
if(vl[j] - w < vl[i]){
vl[i] = vl[j] - w;
}
j = getNextNeighbor(g,g->VerticesList[i],g->VerticesList[j]);
}
}
//vl 的结果看下图b
int e, l;
for(int i = 0; i < n; ++i){
j = getNeighbor(g, g->VerticesList[i]);
while(j != -1){
e = ve[i];
l = vl[j] - getWeight(g, i, j);
if(e == l){
printf("<%c, %c>是关键路径\n",g->VerticesList[i],g->VerticesL\
ist[j]);
}
j = getNextNeighbor(g,g->VerticesList[i],g->VerticesList[j]);
}
}
free(ve);
free(vl);
}
图a

图b

critical_path_main.c
#include "critical_path.h"
int main(){
GraphMtx gm;
//初始化图
init_graph(&gm);
//插入顶点
insert_vertex(&gm, 'A');
insert_vertex(&gm, 'B');
insert_vertex(&gm, 'C');
insert_vertex(&gm, 'D');
insert_vertex(&gm, 'E');
insert_vertex(&gm, 'F');
insert_vertex(&gm, 'G');
insert_vertex(&gm, 'H');
insert_vertex(&gm, 'I');
//添加连线
insert_edge(&gm, 'A', 'B', 6);
insert_edge(&gm, 'A', 'C', 4);
insert_edge(&gm, 'A', 'D', 5);
insert_edge(&gm, 'B', 'E', 1);
insert_edge(&gm, 'C', 'E', 1);
insert_edge(&gm, 'D', 'F', 2);
insert_edge(&gm, 'E', 'G', 9);
insert_edge(&gm, 'E', 'H', 7);
insert_edge(&gm, 'F', 'H', 4);
insert_edge(&gm, 'G', 'I', 2);
insert_edge(&gm, 'H', 'I', 4);
//打印图
show_graph(&gm);
//求解关键路径
critical_path(&gm);
}
编译方法:gcc -g critical_path.c critical_path_main.c




 浙公网安备 33010602011771号
浙公网安备 33010602011771号