c/c++ 图的创建(二维数组法）

c/c++ 图的创建(二维数组法）

图的概念

• 图由点和线组成
• 知道了图中有多少个点，和哪些点之间有线，就可以把一张图描绘出来
• 点之间的线，分有方向和无方向

创建图

创建图，实际就是创建出节点，和节点之间的线，节点和节点之间的线，可以用二维数组，也就是矩阵来表示。

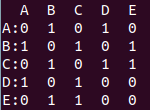
下面的代码实现了上面的图的创建

graph_mtx.h

#include <stdio.h>
#include <malloc.h>
#include <assert.h>

#define Default_vertex_size 10

#define T char//dai biao ding dian de lei xing

typedef struct GraphMtx{
  int MaxVertices;//zui da ding dian shu liang]
  int NumVertices;//shi ji ding dian shu liang
  int NumEdges;//bian de shu lian

  T* VerticesList;//ding dian list
  int** Edge;//bian de lian jie xin xi, bu shi 0 jiu shi 1
}GraphMtx;

//chu shi hua tu
void init_graph(GraphMtx* gm);
//打印二维数组
void show_graph(GraphMtx* gm);
//插入顶点
void insert_vertex(GraphMtx* gm, T v);
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2);
//删除顶点
void remove_vertex(GraphMtx* gm, T v);
//删除顶点间的线
void remove_edge(GraphMtx* gm, T v1, T v2);
//摧毁图
void destroy_graph(GraphMtx* gm);


#endif

graph_mtx.c

#include "graph_mtx.h"

void init_graph(GraphMtx* gm){
  gm->MaxVertices = Default_vertex_size;
  gm->NumEdges = gm->NumVertices = 0;

  //kai pi ding dian de nei cun kong jian
  gm->VerticesList = (T*)malloc(sizeof(T) * (gm->MaxVertices));
  assert(NULL != gm->VerticesList);

  //创建二维数组
  //让一个int的二级指针，指向一个有8个int一级指针的数组
  //开辟一个能存放gm->MaxVertices个int一级指针的内存空间
  gm->Edge = (int**)malloc(sizeof(int*) * (gm->MaxVertices));
  assert(NULL != gm->Edge);
  //开辟gm->MaxVertices组，能存放gm->MaxVertices个int的内存空间
  for(int i = 0; i < gm->MaxVertices; ++i){
    gm->Edge[i] = (int*)malloc(sizeof(int) * gm->MaxVertices);
  }
  //初始化二维数组
  //让每个顶点之间的边的关系都为不相连的
  for(int i = 0; i < gm->MaxVertices; ++i){
    for(int j = 0; j < gm->MaxVertices; ++j){
      gm->Edge[i][j] = 0;
    }
  }
}
//打印二维数组
void show_graph(GraphMtx* gm){
  printf("  ");
  for(int i = 0; i < gm->NumVertices; ++i){
    printf("%c  ", gm->VerticesList[i]);
  }
  printf("\n");
  for(int i = 0; i < gm->NumVertices; ++i){
    //在行首,打印出顶点的名字
    printf("%c:", gm->VerticesList[i]);
    for(int j = 0; j < gm->NumVertices; ++j){
      printf("%d  ", gm->Edge[i][j]);
    }
    printf("\n");
  }
  printf("\n");
}
//插入顶点
void insert_vertex(GraphMtx* gm, T v){
  //顶点空间已满，不能再插入顶点了
  if(gm->NumVertices >= gm->MaxVertices){
    return;
  }
  gm->VerticesList[gm->NumVertices++] = v;
}

//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2){
  if(v1 == v2)return;
  
  int j = -1;
  int k = -1;
  //查找2个顶点的下标
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->VerticesList[i] == v1){
      j = i;
      continue;
    }
    if(gm->VerticesList[i] == v2){
      k = i;
      continue;
    }
  }
  //说明找到顶点的下标了
  if(j != -1 && k != -1){
    //因为是无方向，所以更新2个值
    gm->Edge[j][k] = gm->Edge[k][j] = 1;
    //边数加1
    gm->NumEdges++;
  }
}

graph_mtxmain.c

#include "graph_mtx.h"

int main(){
  GraphMtx gm;
  //初始化图
  init_graph(&gm);
  //插入顶点
  insert_vertex(&gm, 'A');
  insert_vertex(&gm, 'B');
  insert_vertex(&gm, 'C');
  insert_vertex(&gm, 'D');
  insert_vertex(&gm, 'E');

  insert_edge(&gm, 'A', 'B');
  insert_edge(&gm, 'A', 'D');
  insert_edge(&gm, 'B', 'C');
  insert_edge(&gm, 'B', 'E');
  insert_edge(&gm, 'C', 'E');
  insert_edge(&gm, 'C', 'D');

  //顶点和顶点之间的连线关系
  show_graph(&gm);
}