处理了二进制的整数运算，下面我们来进行令人绝望的浮点数运算
我们先来看一下float事列程序：
#include<"stdio.sh">
int main()
{
float sun=0;
for(int i=0;i<100;i++)
{
sun+=0.1;
}
printf("%f",sun);
return 0;
}
这是一个比较简单的C语言循环，可能有没接触过C语言的同学，不要紧，这个程序的大致意思是让这个sum值循环100次，每次加0.1，我们思考下程序的运行结果，我想大多数人都会觉得程序会输出10，接下来我们放到程序中运行一下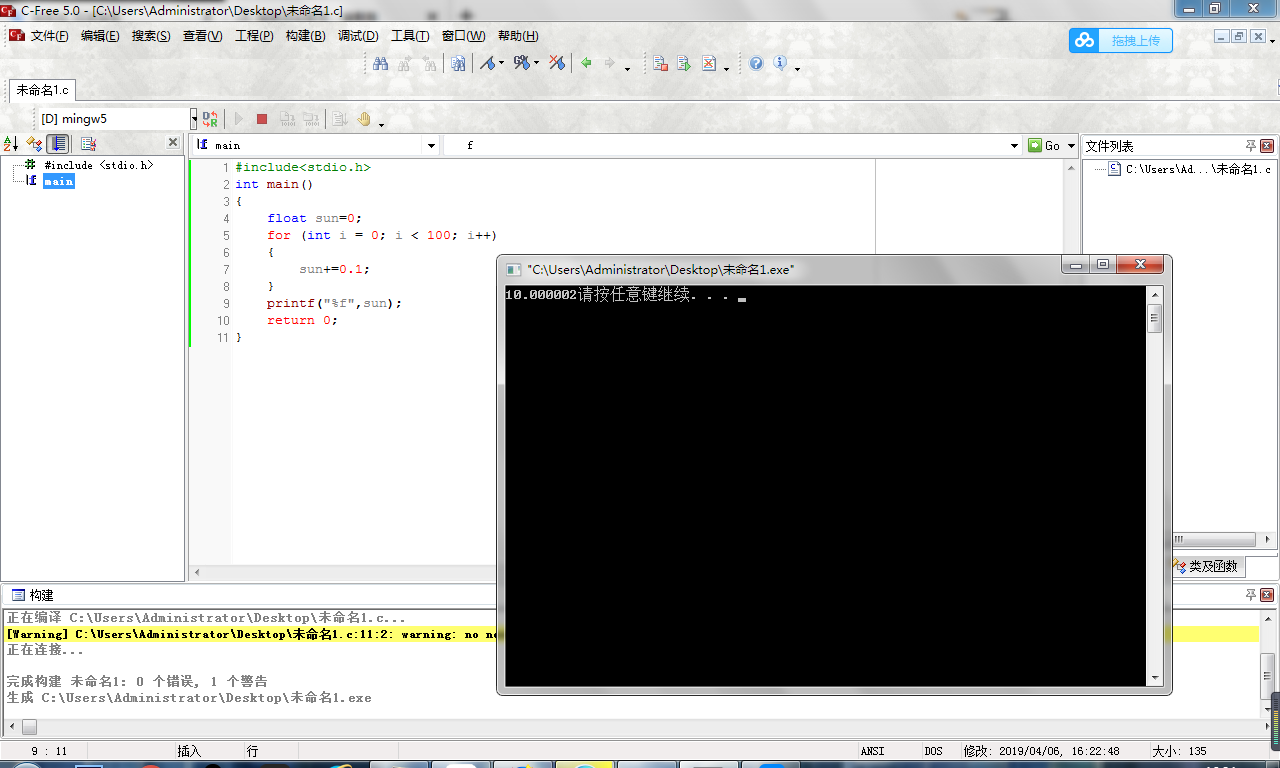
emmmmm....看来结果并非我们的预期，为什么会出现这种情况?这里我们需要了解到一个概念
二进制是如何表示小数的？
例如二进制：1011.0011
小数点前正常计算，小数点后面按照二的负一次方，二的负二次方等等以此类推
这样我们就有了一个问题，二的负一次方二的负二次方等等依次表示0.5,0.25,0.125等等等等这些数值，那么我们如何用二进制表示类似0.9这样的数值呢？
我们可以用二的负二次方加上二的负二次方以此类推，直到加到无限接近于0.9的这个数值为止，但是我们得到的这个数值永远无法等于0.9，这就是为什么我们的计算机再计算我们上面的循环中会出现误差的原因
就好比我们是在向天平中放置筹码，每增加一个筹码就无限接近于平行，但是永远也无法精准的测量出物体的值
我们了解了二进制表达小数的不足之后，也要知道计算机是如何实现二进制的，计算机里是没有小数点位的，那么我们怎么实现浮点数在计算机当中的实现的呢？这里我们就引入了一个IEEE编码，IEEE将内存分为几大块，转化完后生成10110011，将小数点左移，移到最前面1的位置，01100110000....放到32位里面，拿1与127进行运算，当然这些了解就OK，我们需要记住的是，IEEE编码存储浮点数，0.1x100不等于10怎样处理？
我们了解到，计算机中的浮点数运算时及其不安全的，那么我们怎样让0.1x100等于10呢?我们将我们的程序稍微改动一下：
#include<stdio.h>
int main()
{
float sun=0
for (int i=0;i<100;i++)
{
sun+=0.1*10;
}
printf("%f",sun/10);
return 0;
}
ok我们现在来看下结果
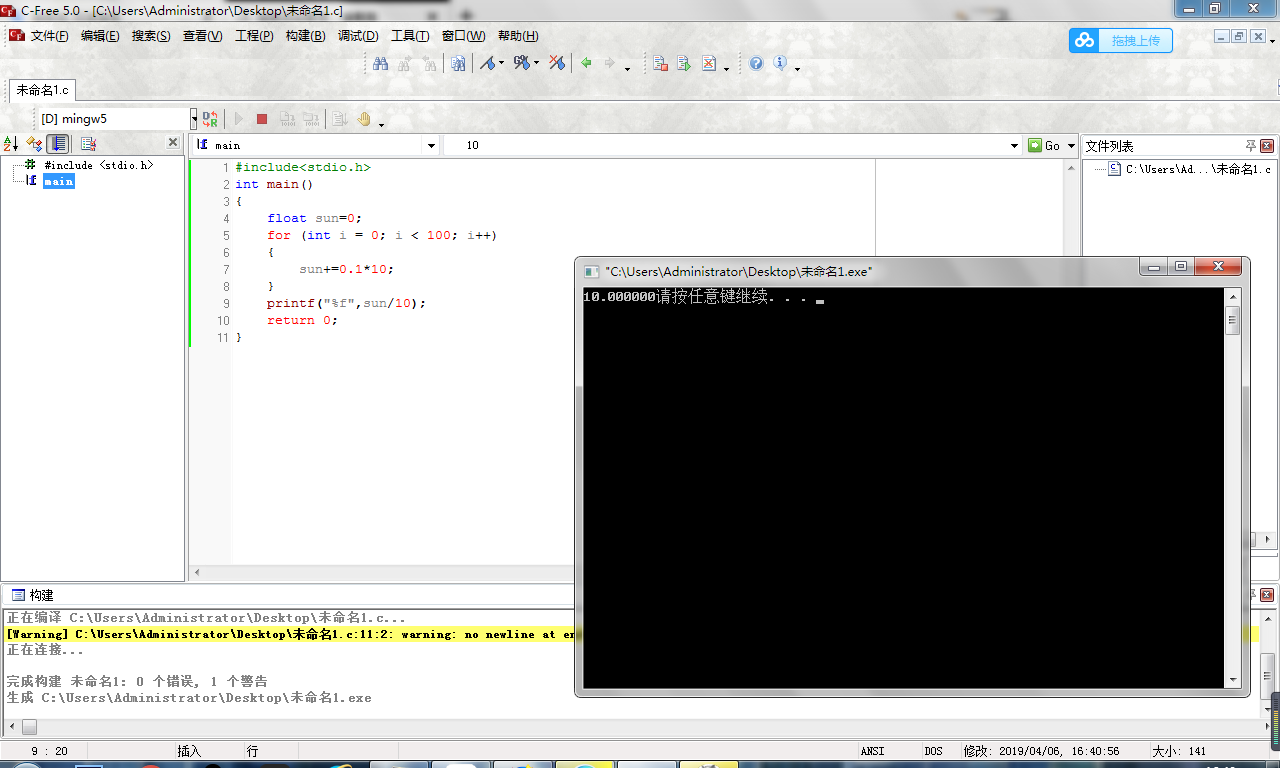
大家应该都看懂程序的意思了吧？既然我们的浮点数无法实现正确输出，那么我们就将我们的浮点数变为正整数，在输出的时候再变回浮点数，在这种情况下，我们就可以实现正确运算了！
当然，出现这种极端情况我们有两种处理办法
- 当整数运算
- 忽略
当整数运算我们可以理解，那么忽略呢？因为我们大多数的浮点数计算误差不会对程序造成影响，所以这种情况我们一般选择忽略
通过这一章我们了解了浮点数的实现和误差处理办法，浮点数在计算机当中是不安全的
