Leetcode刷题第十一天-动态规划
🤯🤯🤯跟着卡哥开启动态规划之旅 代码随想录 (programmercarl.com) 🤯🤯🤯
动态规划五步:
1、确定dp数组(dp table)以及下标的含义
2、确定递推公式
3、dp数组如何初始化
4、确定遍历顺序
5、举例推导dp数组
509:斐波那契数

1 class Solution: 2 def fib(self, n: int) -> int: 3 #dp[i]第i个斐波那契数的数值为dp[i] 4 #推到公式dp[i]=dp[i-1]+dp[i-1] 5 #dp数组初始化dp[0]=0,dp[1]=1 6 #遍历顺序 从前向后 7 #打印dp数组 8 if(n<2): return n 9 dp=[0,1] 10 for i in range(2,n+1): 11 dp.append(dp[i-1]+dp[i-2]) 12 return dp[n]
70:爬楼梯

1 class Solution: 2 def climbStairs(self, n: int) -> int: 3 #dp[i]第i个台阶有dp[i]方法 4 #推到公式dp[i]=dp[i-1]+dp[i-2] 5 #dp数组初始化dp[0]=1,dp[1]=2 6 #遍历顺序 从前向后 7 #打印dp数组 8 dp=[1,2] 9 if(n<3): return dp[n-1] 10 for i in range(2,n): 11 dp.append(dp[i-1]+dp[i-2]) 12 return dp[n-1] 13
746:使用最小花费爬楼梯
链接:746. 使用最小花费爬楼梯 - 力扣(LeetCode)

1 class Solution: 2 def minCostClimbingStairs(self, cost: List[int]) -> int: 3 #dp[i]到i个台阶最小消耗dp[i] 4 #推到公式dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]) 5 #dp数组初始化dp[0]=0,dp[1]=0 6 #遍历顺序 从前向后 7 #打印dp数组 8 dp=[0,0] 9 for i in range(2,len(cost)+1): 10 dp.append(min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])) 11 print(dp[i]) 12 return dp[len(cost)]
62:不同路径
从0开始遍历时,dp数组中值为1的位置需要跳过,只能向下或向右,第一行和第一列的每个格子均只有1种情况,跳过
也可以从1开始遍历

1 class Solution: 2 def uniquePaths(self, m: int, n: int) -> int: 3 #dp[i][j]到ijw位置有dp[i][j]方法 4 #推到公式dp[i][j]=dp[i-1][j]+dp[i][j-1] 5 #dp数组初始化dp[i][0]=1,dp[0][j]=1 6 #遍历顺序 从前向后 7 #打印dp数组 8 dp=[[0 for i in range(n)] for j in range(m)] 9 for i in range(m): dp[i][0]=1 10 for i in range(n): dp[0][i]=1 11 for i in range(m): 12 for j in range(n): 13 if not dp[i][j]: 14 dp[i][j]=dp[i-1][j]+dp[i][j-1] 15 return dp[m-1][n-1]
for i in range(1,m): for j in range(1,n): dp[i][j]=dp[i-1][j]+dp[i][j-1]
63:不同路径II
与62的区别:初始化时如果第一行第一列有障碍,那么障碍后面的格子值为0

1 class Solution: 2 def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int: 3 #dp[i][j]到ijw位置有dp[i][j]方法 4 #推到公式dp[i][j]=dp[i-1][j]+dp[i][j-1] 5 #dp数组初始化dp[i][0]=1,dp[0][j]=1,如果遇到当前位置遇到obstacleGrid[i][0]=1,obstacleGrid[0][i]=1,dp下面保持0 6 #遍历顺序 从前向后 7 #打印dp数组 8 m,n=len(obstacleGrid),len(obstacleGrid[0]) 9 dp=[[0 for i in range(n)] for i in range(m)] 10 for i in range(m): 11 if not obstacleGrid[i][0]: dp[i][0]=1 12 else: break 13 for i in range(n): 14 if not obstacleGrid[0][i]: dp[0][i]=1 15 else: break 16 for i in range(1,m): 17 for j in range(1,n): 18 if(obstacleGrid[i][j]): dp[i][j]=0 19 else: dp[i][j]=dp[i-1][j]+dp[i][j-1] 20 return dp[m-1][n-1]
343:整数拆分
推导公式dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]) for j in range(i)),拆俩数:j,i-j;拆3个数以上j,dp[i-j](至少是拆俩数的情况)

1 class Solution: 2 def integerBreak(self, n: int) -> int: 3 #dp[i]拆分成i个数的最大乘积 4 #推到公式dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]) for j in range(i)) 5 #拆俩数:j,i-j;拆3个数以上j,dp[i-j](至少是拆俩数的情况) 6 #dp数组初始化dp[2]=1,dp[1]=0,dp=[0]=0 7 #遍历顺序 从前向后,从3开始 8 #打印dp数组 9 dp=[0,0,1] 10 for i in range(3,n+1): 11 num=0 12 #遍历到i的一半即可 13 for j in range(1,i//2 +1): 14 num=max(num,max(j*(i-j),j*dp[i-j])) 15 dp.append(num) 16 return dp[n] 17 ''' 18 #贪心 19 sums=1 20 middle=n//2 +1 21 for i in range(2,n): 22 num=n//i 23 sums=max(sums,(num**(i-n%i))*((num+1)**(n%i))) 24 return sums 25 ''' 26
96:不同二叉搜索数
链接:96. 不同的二叉搜索树 - 力扣(LeetCode)

1 class Solution: 2 def numTrees(self, n: int) -> int: 3 #dp[i]由i个数组成的二叉搜索数情况 4 #推导公式dp[i]=sum(dp[i-j]*dp[j-1]) j为头节点 5 #dp数组初始化dp[0]=1,dp[1]=1,dp=[2]=2 6 #遍历顺序 从前向后,从3开始 7 #打印dp数组 8 dp=[1,1,2] 9 for i in range(n-2): dp.append(0) 10 for i in range(3,n+1): 11 for j in range(1,i+1): 12 dp[i]+=dp[i-j]*dp[j-1] 13 return dp[n]
🤯🤯🤯🤯背个背包吧🤯🤯🤯🤯(●'◡'●)(●'◡'●)从卡哥那偷个图φ(゜▽゜*)♪φ(゜▽゜*)♪
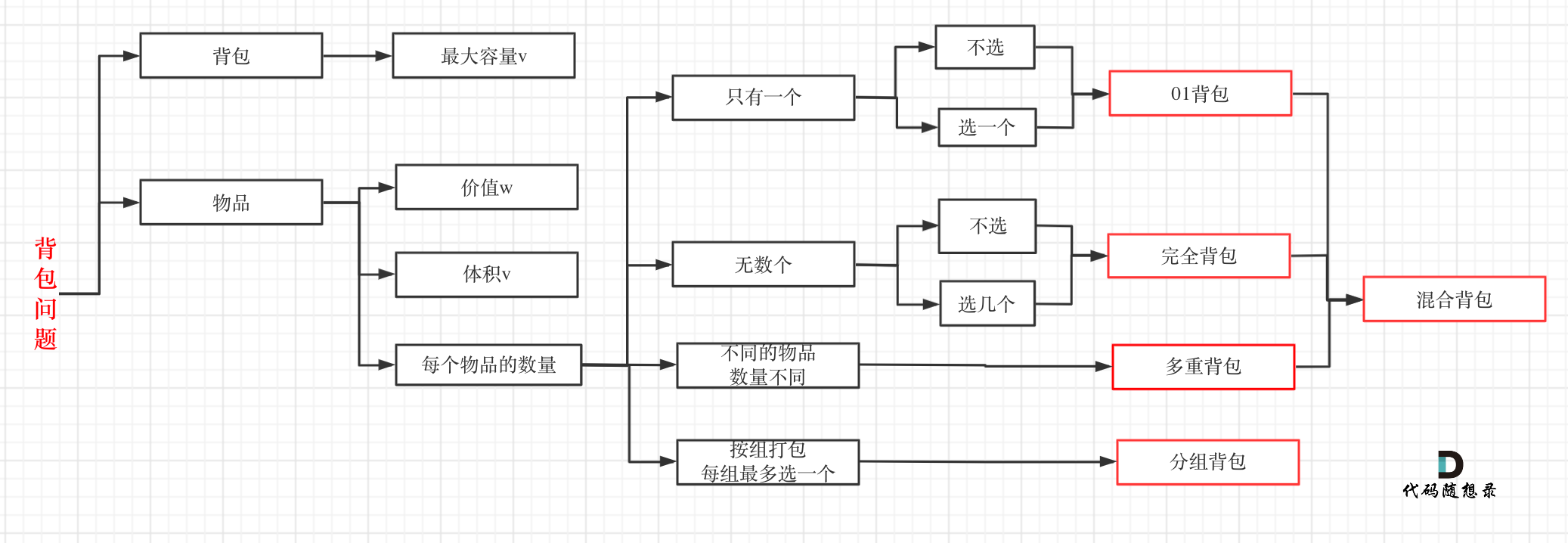
背包分类:
0-1背包:n种物品,每个物品只有一个
完全背包:n种物品,每个物品有无限个
多重背包:n种物品,每个物品个数不同
0-1背包:
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的空间,并且具有不同的价值。
小明的行李空间为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料只能选择一次,并且只有选与不选两种选择,不能进行切割。
第一行包含两个正整数,第一个整数 M 代表研究材料的种类,第二个正整数 N,代表小明的行李空间。
第二行包含 M 个正整数,代表每种研究材料的所占空间。
第三行包含 M 个正整数,代表每种研究材料的价值。

#dp[i][j]空间大小为i得背包可以放入材料得最大价值 #推导公式dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]) #dp数组初始化dp[0][j]=0,dp[i][0]=v[0] #遍历顺序 #打印dp数组 def bag(m,n,w,v): dp=[[0 for i in range(n+1)] for i in range(m)] for i in range(n+1): if(i>=w[0]): dp[0][i]=v[0] #遍历物品 for i in range(1,m): #遍历背包 for j in range(n+1): if(j<w[i]): dp[i][j]=dp[i-1][j] else: dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]) print(dp[m-1][n]) #return dp[m-1][n] m,n=map(int,input().strip().split(' ')) w=list(map(int,input().strip().split())) v=list(map(int,input().strip().split())) bag(m,n,w,v)

1 #dp降维度一维数组,第一个物品遍历完,将所有背包容量覆盖到第二个物品中 2 #推导公式dp[i][j]=max(dp[j], dp[j - w[i]] + v[i]) 3 def bag1(m,n,w,v): 4 #容量为j的背包可以放的最大价值,初始化为0 5 dp=[0 for j in range(n+1)] 6 #遍历物品 7 for i in range(m): 8 #遍历背包,从后往前遍历,一个物品只放一次 9 for j in range(n,w[i]-1,-1): 10 dp[j] = max(dp[j], dp[j - w[i]] + v[i]) 11 print(dp[n])
416:分割等和子集

1 class Solution: 2 def canPartition(self, nums: List[int]) -> bool: 3 #dp[i]容量为i的背包所能放的最大价值,背包最大容量为sum(nums)//2 4 #推导公式dp[i]=max(dp[i], dp[i-num]+num),nums数据组第i个元素即表示物品重量又表示物品价值,w,v 5 #dp数组初始化dp=[0]*n 6 #遍历顺序:背包倒序 7 #打印dp数组 8 sums=sum(nums) 9 if(sums%2==1): return False 10 n=sums//2 11 dp=[0]*(n+1) 12 #遍历物品 13 for num in nums: 14 #遍历背包 15 for i in range(n,num-1,-1): 16 dp[i]=max(dp[i], dp[i-num]+num) 17 if(dp[n]==n): return True 18 return False 19



 浙公网安备 33010602011771号
浙公网安备 33010602011771号