卷积神经网络-填充与步幅

一、前言

1、有时，在应用连续的卷积之后，我们最终得到的输出远小于输入大小。这是由于卷积核的宽度和高度通常大于1所导致的。比如，一个 240×240像素的图像，经过 10 层 5×5的卷积后，将减少到 200×200 像素。如此一来，原始图像的边界丢失了许多有用的信息。而填充是解决此问题的最有效的方法。

2、有时，我们希望大幅度降低图像的宽度和高度。例如，如果我们发现原始的输入分辨率十分冗余。步幅则可以在这类情况下提供帮助。

 

二、填充（padding）

1、在输入图像的边界填充元素（通常需填充元素是0）

2、举例说明：我们将 3×3 输入填充到 5×5。那么它的输出就增加为 4×4。阴影部分是第一个输出元素以及用于输出计算的输入和核张量元素： 0×0+0×1+0×2+0×3=0。

 

 

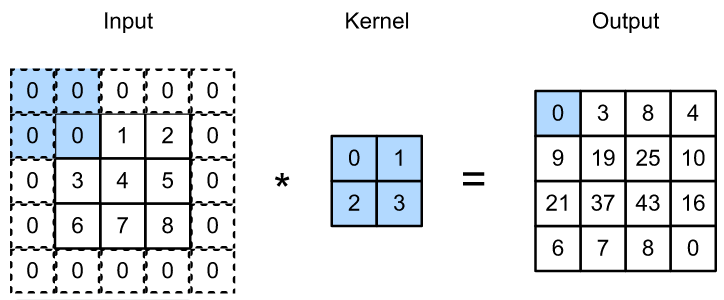
3、举例实现

1、我们创建一个高度和宽度为3的二维卷积层，并(在所有侧边填充1个像素)。给定高度和宽度为8的输入，（通过填充）输出的高度和宽度也是8。

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

import torch from torch import nn   # 为了方便起见，我们定义了一个计算卷积层的函数。 # 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数 def comp_conv2d(conv2d, X):     # 这里的（1，1）表示批量大小和通道数都是1     print(X)           X = X.reshape((1, 1) + X.shape)     # 根据输出可以发现由二维变成四维     print(X)                 Y = conv2d(X)     print(Y)     # 可以发现输出信息格式为([1, 1, 8, 8])     print(Y.shape)           # 省略前两个维度：批量大小和通道     print(Y.shape[2:])     print(Y.reshape(Y.shape[2:]))     # 经过reshape（）可以将信息从四维转为二维     return Y.reshape(Y.shape[2:])     # 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列   # 构建一个卷积层，创建一个高度和宽度都为3的卷积核 # padding表示补零，在原始输入的上下左右边均补一行 conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)   # 随机生成X X = torch.rand(size=(8, 8)) comp_conv2d(conv2d, X).shape

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

# 输出结果<br>tensor([[0.6362, 0.1474, 0.1279, 0.0946, 0.3892, 0.7422, 0.2253, 0.7159],         [0.3365, 0.9141, 0.6993, 0.2646, 0.2851, 0.9957, 0.1081, 0.5389],         [0.1311, 0.0050, 0.7707, 0.5294, 0.2110, 0.6913, 0.6617, 0.4277],         [0.5884, 0.4176, 0.3558, 0.0330, 0.4831, 0.5956, 0.0661, 0.0021],         [0.8887, 0.9830, 0.9509, 0.4214, 0.9846, 0.2628, 0.2390, 0.9926],         [0.7459, 0.7546, 0.9434, 0.1711, 0.1424, 0.6470, 0.6081, 0.0223],         [0.7706, 0.0991, 0.5976, 0.4982, 0.4110, 0.2546, 0.9742, 0.6559],         [0.0258, 0.8337, 0.5379, 0.7532, 0.6330, 0.4920, 0.7403, 0.9212]]) tensor([[[[0.6362, 0.1474, 0.1279, 0.0946, 0.3892, 0.7422, 0.2253, 0.7159],           [0.3365, 0.9141, 0.6993, 0.2646, 0.2851, 0.9957, 0.1081, 0.5389],           [0.1311, 0.0050, 0.7707, 0.5294, 0.2110, 0.6913, 0.6617, 0.4277],           [0.5884, 0.4176, 0.3558, 0.0330, 0.4831, 0.5956, 0.0661, 0.0021],           [0.8887, 0.9830, 0.9509, 0.4214, 0.9846, 0.2628, 0.2390, 0.9926],           [0.7459, 0.7546, 0.9434, 0.1711, 0.1424, 0.6470, 0.6081, 0.0223],           [0.7706, 0.0991, 0.5976, 0.4982, 0.4110, 0.2546, 0.9742, 0.6559],           [0.0258, 0.8337, 0.5379, 0.7532, 0.6330, 0.4920, 0.7403, 0.9212]]]]) tensor([[[[-0.4313, -0.7062, -0.5187, -0.3434, -0.3701, -0.6230, -0.5054,            -0.4642],           [-0.1888, -0.5298, -0.7691, -0.5810, -0.3028, -0.7847, -0.7687,            -0.5896],           [-0.3065, -0.4145, -0.5818, -0.6790, -0.4038, -0.6081, -0.6130,            -0.5209],           [-0.5489, -0.7055, -0.7460, -0.7536, -0.5167, -0.6074, -0.7524,            -0.6743],           [-0.4373, -0.9133, -0.9603, -0.5149, -0.4895, -0.8844, -0.4940,            -0.4338],           [-0.3335, -0.7048, -0.9772, -0.8000, -0.5281, -0.6514, -0.7168,            -0.8032],           [-0.3584, -0.7302, -0.7864, -0.8732, -0.5824, -0.4955, -0.8362,            -0.9583],           [-0.1615, -0.2958, -0.3974, -0.4630, -0.5202, -0.2874, -0.3625,            -0.7945]]]], grad_fn=<ThnnConv2DBackward>) torch.Size([1, 1, 8, 8]) torch.Size([8, 8]) tensor([[-0.4313, -0.7062, -0.5187, -0.3434, -0.3701, -0.6230, -0.5054, -0.4642],         [-0.1888, -0.5298, -0.7691, -0.5810, -0.3028, -0.7847, -0.7687, -0.5896],         [-0.3065, -0.4145, -0.5818, -0.6790, -0.4038, -0.6081, -0.6130, -0.5209],         [-0.5489, -0.7055, -0.7460, -0.7536, -0.5167, -0.6074, -0.7524, -0.6743],         [-0.4373, -0.9133, -0.9603, -0.5149, -0.4895, -0.8844, -0.4940, -0.4338],         [-0.3335, -0.7048, -0.9772, -0.8000, -0.5281, -0.6514, -0.7168, -0.8032],         [-0.3584, -0.7302, -0.7864, -0.8732, -0.5824, -0.4955, -0.8362, -0.9583],         [-0.1615, -0.2958, -0.3974, -0.4630, -0.5202, -0.2874, -0.3625, -0.7945]],        grad_fn=<ViewBackward>) torch.Size([8, 8])

2、当内核的高度和宽度不同时，我们可以填充不同的高度和宽度，使输出和输入具有相同的高度和宽度

?

1 2 3

# padding：上下加相同的行，左右加相同的行 conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1)) comp_conv2d(conv2d, X).shape

　　

三、步幅（stride）

1、在计算互相关时，卷积窗口从输入张量的左上角开始，向下和向右滑动。在之前的例子中，默认滑动一个元素。但是，有时候为了高效计算和缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。我们将每次滑动元素的数量称为步幅（stride）

2、举例说明：使用垂直步幅为 3，水平步幅为 2 的二维互相关运算，当卷积窗口继续向右滑动两列时，没有输出，因为输出元素无法填充窗口

 

 

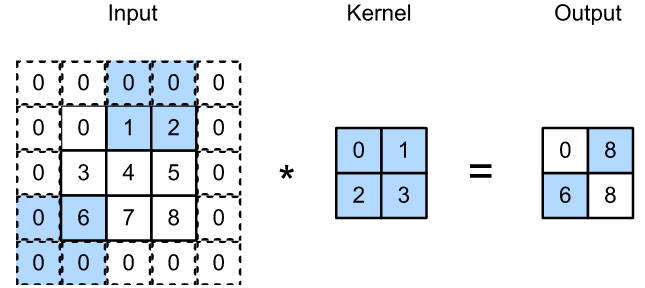
3、代码实现

?

1 2 3

# stride参数：设置输入的高度和宽度 conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2) comp_conv2d(conv2d, X).shape

?

1	#输出结果<br><br>torch.Size([4, 4])

　　

?

1 2	conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4)) comp_conv2d(conv2d, X).shape

?

1 2 3

#输出结果   torch.Size([2, 2])

　　

四、小结

1、填充可以增加输出的高度和宽度。这常用来使输出与输入具有相同的高和宽

2、步幅可以减小输出的高和宽。

3、填充和步幅可用于有效的调整数据的维度