卷积神经网络-二维卷积层

一、前言

1、空间不变性：我们使用的无论哪种方法都应该和物体的位置无关

局部性：神经网络的底层应该只探索输入图像中的局部区域，而不考虑图像远处区域的内容，这就是“局部性”原则
平移不变性：不管出现在图像中的哪个位置，神经网络的底层应该对相同的图像区域做类似的相应

2、卷积神经网络（convolutional neural network）：是含有卷积层（convolutional layer）的神经网络

二、二维互作运算

1、虽然卷积运算得名于卷积（convolution）运算，但我们通常在卷积层中使用更加直观的互相关（cross-correlation）运算

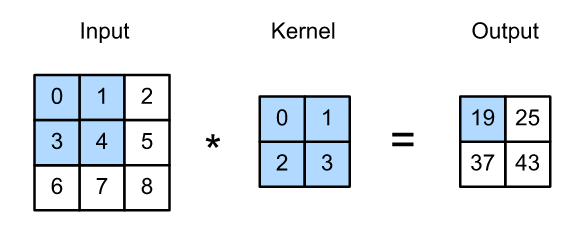
2、基本概念

输入是一个高和宽均为3的二维数组，记作为（3，3）
核数组的高和宽都是2，该数组在卷积计算中又称为卷积核或过滤器
卷积核窗口（卷积窗口）的形状取决于卷积核的高和宽

3、在二维互相关运算中，卷积窗口从输入数组的最左上方开始，按从左往右、从上往下的顺序依次在输入数组中滑动。当卷积窗口滑动到某一位置时，窗口中的输入子数组与核数组按元素相乘并求和，得到输出数组中相应位置的元素。

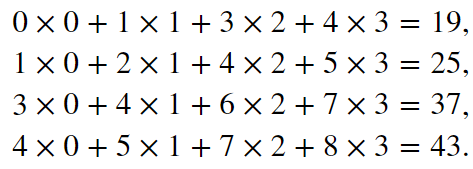
4、输出大小

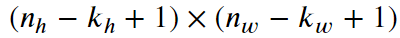
输入形状：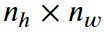

卷积核窗口形状：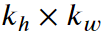

$k_{h} \times k_{w}$

import torch
from torch import nn
from d2l import torch as d2l

# 返回互相关运算后的输出张量
def corr2d(X, K):  #@save
    """计算二维互相关运算。"""
    # K是核矩阵。h、w就是行数和列数
    h, w = K.shape
    
    # 定义输出矩阵的大小
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    
    # 双重嵌套，给输出矩阵赋值
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

2、通过输入张量X和卷积核张量K，来验证上述二维互相关运算的输出

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print(type(K.shape))

corr2d(X, K)

#输出结果

<class 'torch.Size'>
tensor([[19., 25.],
        [37., 43.]])

四、卷积层

1、卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出

2、卷积层中的两个被训练的参数是卷积核权重和标量偏置。

3、像我们之前随机初始化全连接层一样，在训练基于卷积层的模型时，我们也随机初始化卷积核权重。

class Conv2D(nn.Module):
    # kernel_size：超参数
    def __init__(self, kernel_size):
        super().__init__()
        
        # torch.rand：均匀分布，从区间[0, 1)中抽取的一组随机数（返回一个张量）
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        # 将X与self.weight进行互相关运算计算输出张量+偏置量
        return corr2d(x, self.weight) + self.bias

五、图像中物体边缘检测

卷积层的简单应用——检测图像中物体的边缘，即找到像素变化的位置

1、首先，构造一个

# 用张量表示图像
X = torch.ones((6, 8))
X[:, 2:6] = 0
X
print(X.T)

#输出结果

tensor([[1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1.],
        [0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0.],
        [1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1.]])

2、接下来，构造一个高度为

K = torch.tensor([[1.0, -1.0]])

3、对参数 X（输入）和我们设计的卷积核 K 执行互相关运算

Y = corr2d(X, K)
Y

#输出结果

tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

4、可以发现，输出Y中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘。其它情况输出为0

5、注意：卷积核K只可以检测垂直边缘

六、学习卷积核

1、通过查看“输入-输出”对来学习由 X 生成 Y 的卷积核。

2、首先，先构造一个卷积层，并将其卷积核初始化为随机张量。

3、每次迭代中，我们比较 Y 与卷积层输出的平方误差，然后计算梯度来更新卷积核。

'''
nn.Conv2d的功能是：对由多个输入平面组成的输入信号进行二维卷积
输入信号的形式：[ batch_size, channels, height_1, width_1 ]
1、batch_size:一个batch中样例的个数
2、channels ：通道数，也就是当前层的深度
3、height_1：图片的高
4、width_1：图片的宽

'''


# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
# 第一个1是输入通道，第二个1是输出通道
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
print(conv2d)
print(conv2d.weight)
print(conv2d.bias)

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
print(X)
print(Y)

print('----------')
# X是输入，Y是输出
# 在学习卷积核中，可以通过查看“输入-输出”对老学习由X生成Y的卷积核
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
print(X)
print(Y)

for i in range(10):
    # 卷积层输出
    Y_hat = conv2d(X)
    
    # 在每次迭代中，比较真实输出Y与卷积层输出的平方误差
    l = (Y_hat - Y)**2
    
    conv2d.zero_grad()
    # 然后计算梯度
    l.sum().backward()
    # 迭代（更新）卷积核
    conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'batch {i+1}, loss {l.sum():.3f}')

4、查看所学的卷积核的权重张量

conv2d.weight.data.reshape((1, 2)),K

#输出结果

(tensor([[ 0.9765, -1.0093]]), tensor([[ 1., -1.]]))

七、特征图和感受野

1、二维卷积层输出的二维数组可以看作输入在空间维度（宽和高）上某一级的表征，也叫特征图

2、影响元素x的前向计算的所所有可能输入区域（可能大于输入的实际尺寸），叫做x的感受野。

3、我们可以通过更深（嵌套使用）的卷积神经网络使特征图中单个元素的感受野变得更加广阔，从而捕捉输入上更大尺寸的特征。

八、小结

1、二维卷积层的核心计算是二维互相关运算。最简单的形式是，对二维输入数据和卷积核执行互相关操作，然后添加一个偏置。

2、可以设计一个卷积核来检测图像的边缘

3、可以从数据中学习卷积核的参数。

4、核矩阵的大小是超参数。核矩阵和偏移是可学习的参数

posted @ 2021-08-03 20:58 小秦同学在上学阅读(972) 评论(0) 编辑收藏举报

刷新页面返回顶部

卷积神经网络-二维卷积层

公告