权重衰减从零开始实现

一、生成数据集

?

1 2 3 4 5

#权重衰退是最广泛使用的正则化的技术之一 %matplotlib inline import torch from torch import nn from d2l import torch as d2l

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

#𝜖 where 𝜖∼(0,0.012)：表示噪音，是一个均值为0，方差为0.01的正态分布   #n_train：训练样本。n_test：测试样本。 n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5   # 真实的w和b # true_w：是一个200*1的矩阵，矩阵内容全为0.01 true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05     # synthetic_data：合成数据集 # train_data：是一个包含20个样本的训练数据集 train_data = d2l.synthetic_data(true_w, true_b, n_train) train_iter = d2l.load_array(train_data, batch_size)     # test_data：是一个包含100个样本的测试数据集 test_data = d2l.synthetic_data(true_w, true_b, n_test) test_iter = d2l.load_array(test_data, batch_size, is_train=False)

　

二、初始化参数模型

?

1 2 3 4 5 6

def init_params():     #初始化w,w是一个均值为0方差为1。长度为200*1的向量     w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)     #初始化b，是一个全0的标量     b = torch.zeros(1, requires_grad=True)     return [w, b]

　　

三、定义L2范数惩罚

?

1 2 3

#L2范数的实现，w中每个向量的平方和除以2 def l2_penalty(w):     return torch.sum(w.pow(2)) / 2

 

四、训练代码实现

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

#lambd超参数   def train(lambd):     # init_params：初始化权重w和方差b     w, b = init_params()     print(w)     print(b)           # linreg：线性回归     # squared_loss：平方损失函数     # lambda函数也称为匿名函数（在这里相当于定义模型） https://www.cnblogs.com/curo0119/p/8952536.html     net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss                 # num_epochs：表示迭代次数；lr=0.003：表示学习率     num_epochs, lr = 100, 0.003     animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',                             xlim=[5, num_epochs], legend=['train', 'test'])                 for epoch in range(num_epochs):         for X, y in train_iter:             #with torch.enable_grad():                 # 增加了L2范数惩罚项，广播机制使l2_penalty(w)成为一个长度为`batch_size`的向量。                               #lambd * l2_penalty(w)：增加了L2范数惩罚项             l = loss(net(X), y) + lambd * l2_penalty(w)             l.sum().backward()             d2l.sgd([w, b], lr, batch_size)         if (epoch + 1) % 5 == 0:             animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),                                      d2l.evaluate_loss(net, test_iter, loss)))     print('w的L2范数是：', torch.norm(w).item())

　　

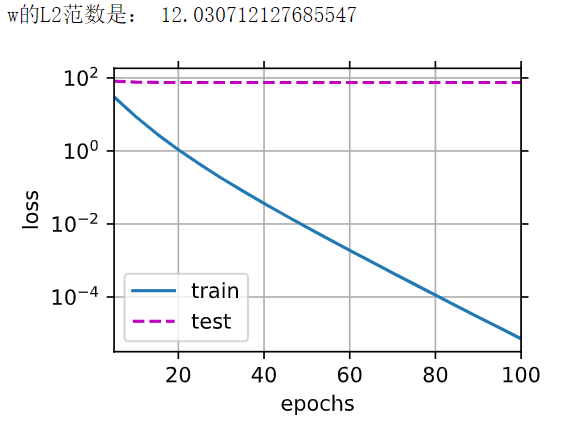
五、忽略正则化直接训练——也就是罚为0

?

1 2 3

train(lambd=0)   #可以发现明显的过拟合

 

 

 

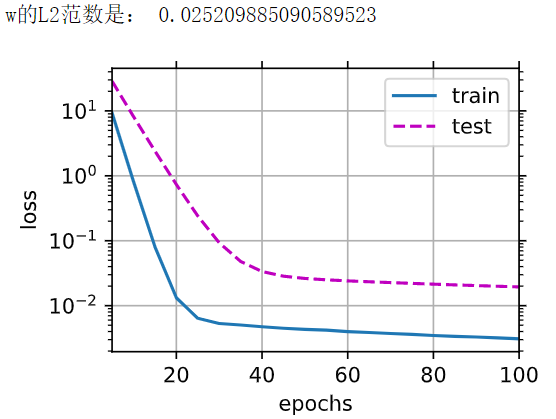
六、使用权重衰减

?

1	train(lambd=10)