多层·感知机

一、前言

1、多层感知机在输出层和输入层之间增加了一个或全连接的隐藏层，并通过激活函数转换隐藏层的输出。

2、常用的激活函数包括ReLU函数、sigmoid函数和tanh函数

 

 

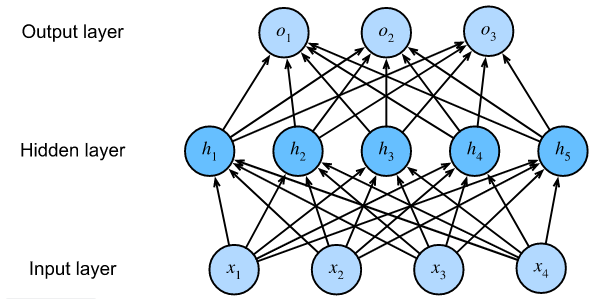
二、隐藏层（hidden layer）

1、多层感知机在单层神经网络的基础上引入了一到多个隐藏层。隐藏层位于输入层到输出层之间

2、图中显示，输入个数为4，输出个数为3。中间的隐藏层中包含了5个隐藏单元（hidden unit）。由于输入层不涉及计算，所以图中的多层感知机的层数为2

3、由图可知，隐藏层中的神经元和输入层中各个输入完全连接，输出层中的神经元和隐藏层中的各个神经元也完全连接。因此多层感知机中的隐藏层和输出层都是全连接层

 

三、合并隐藏层

 

1、从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依旧等价于一个单层神经网络：其中输出层权重参数为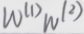，偏差参数为。不难发现，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。

 

 2、在添加隐藏层之后，模型现在需要跟踪和更新额外的参数。可是我们会惊讶地发现：在上面定义的模型里，我们没有好处！原因很简单。上面的隐藏单元由输入的仿射函数给出，而输出（softmax操作前）只是隐藏单元的仿射函数。仿射函数的仿射函数本身就是仿射函数。但是我们之前的线性模型已经能够表示任何仿射函数。

3、为了发挥多层结构的潜力，我们需要在仿射变换之后对每个隐藏单元应用非线性的激活函数。激活函数的输出称为激活值。一般来说，有了激活函数，就不可能把多层感知机退化为线性模型。

四、激活函数

1、ReLU函数：将相应的激活值设为0来仅保留正元素并丢弃所有负元素

?

1 2 3

%matplotlib inline import torch from d2l import torch as d2l

?

1 2 3 4 5

# 生成一个从-8.0到7.9的列表，以0.1为跳跃点 x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)   y = torch.relu(x) d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

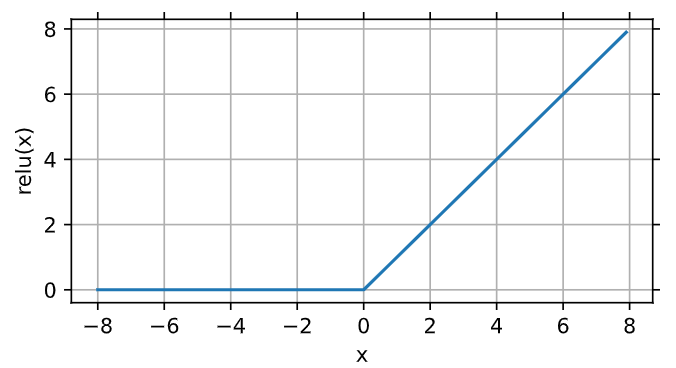
求导：

• 当输入为负时，导数为0
• 当输入为正时，导数为1
• 当输入为0时，没有导数，用左边导数代替（0）

 

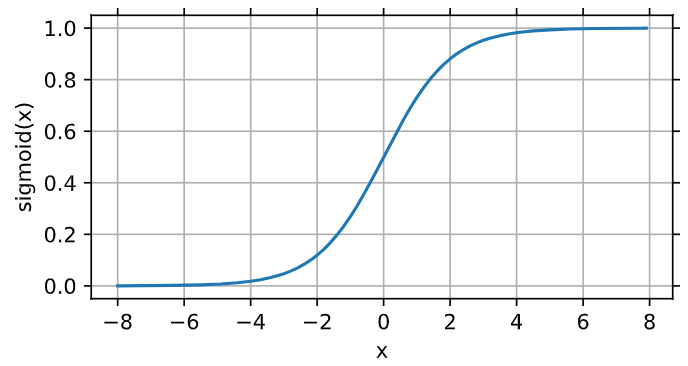
2、 sigmoid函数：将元素的值变为0到1之间

 

?

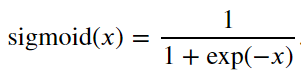
1 2	y = torch.sigmoid(x) d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

 

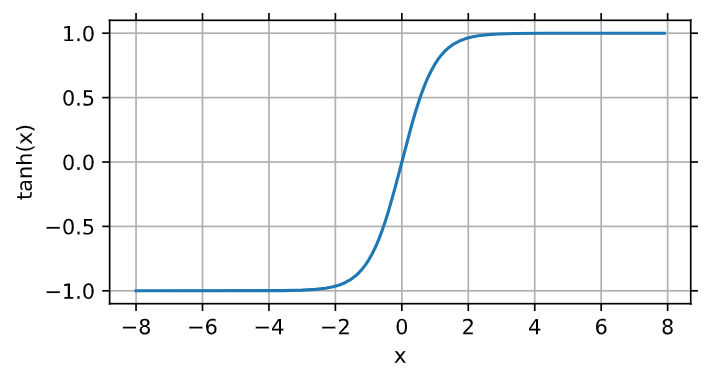
 3、tanh函数：将输入压缩转换到区间(-1, 1)上

 

?

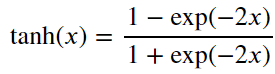
1 2	y = torch.tanh(x) d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))