线性回归从零实现

一、前言

我们将从零开始实现整个方法，包括数据流水线、模型、损失函数和小批量随机梯度下降优化器。虽然现代的深度学习框架几乎可以自动化地进行所有这些工作，但从零开始实现可以确保你真正知道自己在做什么。

例子中我们先用自己设置好的w和b去生成数据集，再用建立的模型去跑数据生成w和b。比较，熟悉流程。

二、生成数据集

1、生成一个包含1000个样本的数据集，每个样本包含从标准正态分布中采样的2个特征。所以生成的样本集合就是一个1000*2的矩阵。使用线性模型参数

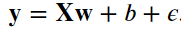
%matplotlib inline

#matplotlib包用于作图，且设置成嵌入显示
import random #因为要随机梯度下降和初始化权重
import torch
from d2l import torch as d2l


#人造数据集：就是知道W与b
#生成数据集
def synthetic_data(w, b, num_examples):  #@save num_example为样本个数
    """生成 y = Xw + b + 噪声。"""
    
    # normal：返回一个张量，包含了从指定均值means和标准差std的离散正态分布中抽取的一组随机数
    X = torch.normal(0, 1, (num_examples, len(w)))   #均值为0，方差为1
    
    # matmul：矩阵乘法
    y = torch.matmul(X, w) + b
    
    # 生成噪音
    y += torch.normal(0, 0.01, y.shape)  #增加复杂度噪音，均值为0，方差为0.01，形状和Y相同
    return X, y.reshape((-1, 1))#reshape函数调用，y=1：说明以列向量返回


#创建训练样本
true_w = torch.tensor([2, -3.4])
true_b = 4.2

# 返回的X就是生成的样本1000*2
# 返回的Y就是输出
features, labels = synthetic_data(true_w, true_b, 1000)#synthetic_data函数来生成特征和标注

print('features:', features[0], '\nlabel:', labels[0])
#第零个样本
#第零个标号，标签可以理解为测试值

#输出结果

features: tensor([-0.4227, -0.1351]) 
label: tensor([3.8342])

3、归纳：

w=[2, -3.4]
b=4.2
样本数据集：tensor（1000*2矩阵，1000个样本，每个样本两个特征）
输出数据集：label（1000*1矩阵，1000个样本的真实输出值）

三、读取数据集

1、在训练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用其来更新模型。所以，我们需要定义一个函数来打乱数据集中的样本并以小批量方式获取数据

# 生成大小为batch_size的小批量
# features：特征矩阵
# labels：标签向量

def data_iter(batch_size, features, labels):
    
    # len()：求矩阵时长度时相当于输出行的数目
    num_examples = len(features)
    indices = list(range(num_examples))#生成标号，列表形式存储
    
    # random.shuffle(列表名)：打乱列表顺序
    random.shuffle(indices)#将下标随机打乱
    
    #构造随机样本。把样本的顺序打乱，然后间隔相同访问，达到随机目的
    for i in range(0, num_examples, batch_size): #从0开始，到num_examples结束，每次跳batch_size个距离
        batch_indices = torch.tensor(
            indices[i:min(i + batch_size, num_examples)])
        
        yield features[batch_indices], labels[batch_indices]
        #yield就是返回一个值，并且记住这个返回的位置，下次迭代就从这个位置开始


batch_size = 10

# feature是样本集，labels是输出集
#给定一个样本标号，每次随机从里面选取1个样本返回出来
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break


#输出结果

tensor([[ 0.5869, -0.4840],
        [-0.5858, -0.2203],
        [-1.3200,  0.8196],
        [-1.4709,  0.3775],
        [ 1.6446, -0.6258],
        [-0.3671,  0.1637],
        [ 0.5638,  0.0109],
        [ 1.5174, -0.7655],
        [ 2.1286, -2.4791],
        [ 1.2452,  0.8433]]) 
 tensor([[ 7.0111],
        [ 3.7876],
        [-1.2331],
        [-0.0249],
        [ 9.6155],
        [ 2.9188],
        [ 5.3045],
        [ 9.8318],
        [16.9045],
        [ 3.8199]])

四、初始化模型参数

在使用小批量随机梯度下降优化我们模型参数之前，我们需要设置超参数

#torch.normal(means, std, out=None)均值，标准差，可选的输出张量

# 此时size就是定义两行一列
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)#requires_grad用于说明当前量是否需要在计算中保留对应的梯度信息
b = torch.zeros(1, requires_grad=True)

五、定义线性模型

def linreg(X, w, b):  #@save
    """线性回归模型。"""
    return torch.matmul(X, w) + b #返回输入X乘以w加上b，就是线性模型

六、定义损失函数

1、在更新w和b之前，需要计算损失函数的梯度，所以需要先定义损失函数

def squared_loss(y_hat, y):  #@save y_hat是预测值，y是真实值
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape))**2 / 2  #y.reshape(y_hat.shape)为了加减方便，将y的形状统一为y_hat

七、定义优化算法

1、本例用小批量随机梯度下降

2、在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度、再朝着减少损失的方向更新我们的参数

3、我们计算的损失是一个批量样本的总和

def sgd(params, lr, batch_size):  #params为模型参数集合，lr为学习率，batch_size:批量大小
    """小批量随机梯度下降。"""
    
    #只是想看一下训练的效果，并不是想通过验证集来更新网络时，就可以使用with torch.no_grad()
    # torch.no_grad()：强制之后的内容不进行计算图构建
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size#param.grad是求梯度
            param.grad.zero_()#因为pytorch不会自动将梯度设置为0，设置为零后下次计算就不会与上次相关了

八、训练

1、训练是用的全部训练集，而不是小批量数据

lr = 0.03#学习率（超参数）
num_epochs = 3#意思是把整个数据扫三遍（超参数）

# linreg：模型生成函数
# squared_loss：均方损失函数
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        
        l = loss(net(X, w, b), y)  # `X`和`y`的小批量损失
        
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()#求和之后算梯度
        
        sgd([w, b], lr, batch_size)  # 小批量梯度更新
        
    with torch.no_grad():# 不用生成计算图
        
        # loss:计算损失
        # labels：真实值
        # net(features, w, b)：预测值
        train_l = loss(net(features, w, b), labels)
        
        # 对1000份材料进行训练，产生1000个误差数据
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
    print(w,b)

#输出结果

epoch 1, loss 0.000051
tensor([[ 2.0002],
        [-3.4010]], requires_grad=True) tensor([4.2001], requires_grad=True)
epoch 2, loss 0.000051
tensor([[ 2.0003],
        [-3.4010]], requires_grad=True) tensor([4.2000], requires_grad=True)
epoch 3, loss 0.000051
tensor([[ 2.0003],
        [-3.4003]], requires_grad=True) tensor([4.1998], requires_grad=True)

2、因为我们使用的是自己创建的的数据集，所以我们知道真正的参数是什么，可以通过比较训练得到的参数与真实参数作比较查看接近程度

posted @ 2021-07-26 16:55 小秦同学在上学阅读(380) 评论(0) 编辑收藏举报

刷新页面返回顶部

线性回归从零实现

公告