线性代数-矩阵乘积

一、点积

概念：相同位置的按元素乘积的和，可以通过dot()函数调用

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

y = torch.ones(4, dtype=torch.float32) print(y) print(x)   # 点积：相同位置的按元素乘积的和 print(torch.dot(x, y))   # 可以通过执行元素乘法，然后进行求和来表示两个向量的点积 print(x*y) print((x*y).sum())   #输出结果   tensor([1., 1., 1., 1.]) tensor([0., 1., 2., 3.]) tensor(6.) tensor([0., 1., 2., 3.]) tensor(6.)

　　

二、矩阵-向量积

1、调用mv函数求矩阵向量积

2、矩阵向量积 𝐀𝐱 是一个长度为 𝑚 的列向量，其第 𝑖 个元素是点积（都是1行n列，可以做点积，最后得到一个标量）

?

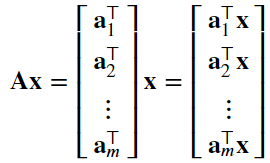
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

# torch.mv是矩阵与向量积   print(A) print(x) print(torch.mv(A,x)) A.shape, x.shape, torch.mv(A, x) # A是5行4列的元素，x是一个有四个元素的向量   #输出结果   tensor([[ 0.,  1.,  2.,  3.],         [ 4.,  5.,  6.,  7.],         [ 8.,  9., 10., 11.],         [12., 13., 14., 15.],         [16., 17., 18., 19.]]) tensor([0., 1., 2., 3.]) tensor([ 14.,  38.,  62.,  86., 110.]) (torch.Size([5, 4]), torch.Size([4]), tensor([ 14.,  38.,  62.,  86., 110.]))

　　

三、矩阵-矩阵乘法

1、调用mm函数求矩阵的乘法

2、注意矩阵乘法与哈达玛积的区别

3、哈达玛积：将两个矩阵按元素乘积

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

# torch.mm：矩阵的乘法，行与列相乘   B = torch.ones(4, 3) print('我是B矩阵\n',B) print('我是A矩阵\n',A)   torch.mm(A, B)   #输出结果   我是B矩阵  tensor([[1., 1., 1.],         [1., 1., 1.],         [1., 1., 1.],         [1., 1., 1.]]) 我是A矩阵  tensor([[ 0.,  1.,  2.,  3.],         [ 4.,  5.,  6.,  7.],         [ 8.,  9., 10., 11.],         [12., 13., 14., 15.],         [16., 17., 18., 19.]]) tensor([[ 6.,  6.,  6.],         [22., 22., 22.],         [38., 38., 38.],         [54., 54., 54.],         [70., 70., 70.]])

　　

四、范数

1、一个向量的范数告诉我们一个向量的大小。这里考虑的大小（size）概念不涉及维度，而是分量的大小

2、L2范数：向量元素平方和的平方根

3、范数只能计算浮点数类型

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

# ‖𝐱‖就是x向量元素平方和的平方根 # 在深度学习中，我们更经常地使用  𝐿2  范数的平方。   u = torch.tensor([3.0, -4.0]) v = torch.tensor([[4,3],[6,8]]) print(u) print(v)     # 使用 norm 来求L2范数 torch.norm(u)   #torch.norm(v):如果对其求范数会报错   #输出结果 tensor([ 3., -4.]) tensor([[4, 3],         [6, 8]]) tensor(5.)

4、L1范数：表示为向量元素的绝对值之和

?

1 2 3 4 5 6 7 8 9 10 11 12 13

# L1范数是向量各元素的绝对值之和 print(u) print(u.abs()) print(abs(u))   torch.abs(u).sum()   #输出结果   tensor([ 3., -4.]) tensor([3., 4.]) tensor([3., 4.]) tensor(7.)

5、弗罗贝尼乌斯范数：计算矩阵元素平方和的平方根

?

1 2 3 4 5 6 7 8

# 弗罗贝尼乌斯范数：可以用来计算矩阵元素平方和的平方根 # 使用norm（）函数来调用   torch.norm(torch.ones((2, 2)))   #输出函数   tensor(2.)