排序---->插入排序
插入排序
插入排序的基本排序思想是:逐个考察每个待排序元素,将每一个新元素插入到前面已经排好序的序列中适当的位置上,使得新序列仍然是一个有序序列。在这一类排序中主要有三种排序方法:直接插入排序、折半插入排序和希尔排序。
2.1直接插入排序
基本思想
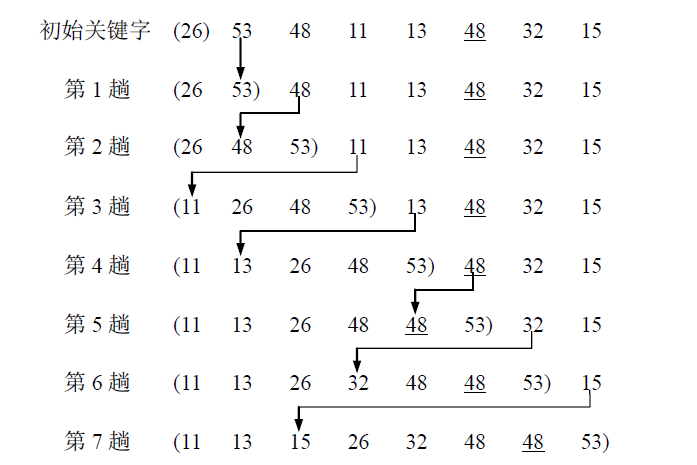
直接插入排序是一种最简单的插入排序方法,它的基本思想是:仅有一个元素的序列总是有序的,因此,对n个记录的序列,可从第二个元素开始直到第n个元素,逐个向有序序列中执行插入操作,第一趟比较前两个数,然后把第二个数按大小插入到有序表中; 第二趟把第三个数据与前两个数从前向后扫描,把第三个数按大小插入到有序表中;依次进行下去,进行了(n-1)趟扫描以后就完成了整个排序过程。从而得到n个元素按关键字有序的序列。一般来说,在含有j-1个元素的有序序列中插入一个元素的方法是:从第j-1个元素开始依次向前搜索应当插入的位置,并且在搜索插入位置的同时可以后移元素,这样当找到适当的插入位置时即可直接插入元素。
举例:
代码实现
代码实现1:
//简单插入排序
public void insertSort(Object[] r, int low, int high){
for (int i=low+1; i<=high; i++)
if (strategy.compare(r[i],r[i-1])<0){ //小于时,需将r[i]插入有序表
Object temp = r[i];
r[i] = r[i-1];
int j=i-2;
for (; j>=low&&strategy.compare(temp,r[j])<0; j--)
r[j+1] = r[j]; //记录后移
r[j+1] = temp; //插入到正确位置
}
}
代码实现2:搜索插入位置的同时没有后移元素,搜索到后一次移动
public class Straight_Insert_Sort {
public static void sort(Comparable array[]) {
int i, j;
Comparable temp;
for (i = 1; i < array.length; i++) {
temp = array[i];
for (j = 0; j < i; j++) {
if (array[j].compareTo(array[i]) > 0) {
for (int k = i; k > j; k--) {
array[k] = array[k - 1];
}
array[j] = temp;
break;
}
}
}
}
public static void main(String[] args) {
Integer array[] = { 46, 58, 15, 45, 90, 18, 10, 62 };
sort(array);
}
}
效率分析
空间效率:仅使用一个辅存单元O(1)。
时间效率:假设待排序的元素个数为n,则向有序表中逐个插入记录的操作进行了n-1趟,每趟操作分为比较关键码和移动记录,而比较的次数和移动记录的次数取决于待排序列按关键码的初始排列。
⑴ 在最好情况下,即待排序序列已按关键字有序,每趟操作只需1次比较0次移动。此时有:
总比较次数 = n-1 次
总移动次数 = 0 次
⑵ 在最坏情况下,即待排序序列按关键字逆序排序,这时在第j 趟操作中,为插入元素需要同前面的j个元素进行j次关键字比较,移动元素的次数为j+1 次。此时有:
总比较次数 ≈ n²/4 次
总移动次数 ≈ n²/4 次
由此,直接插入排序的时间复杂度为O(n²),并且是一个稳定的排序方法。
2.2折半插入排序
基本思想:
对直接插入排序进行改进。直接插入排序的基本操作是向有序序列中插入一个元素,插入位置的确定是通过对有序序列中元素按关键字逐个比较得到的。既然是在有序序列中确定插入位置,则可以不断二分有序序列来确定插入位置,即折半插入排序搜索插入位置的方法可以使用折半查找实现。
例子:
代码实现:
代码实现1:
//折半插入排序
public void binInsertSort(Object[] r, int low, int high){
for (int i=low+1; i<=high; i++){
Object temp = r[i]; //保存待插入元素
int hi = i-1; int lo = low; //设置初始区间
while (lo<=hi){ //折半确定插入位置
int mid = (lo+hi)/2;
if(strategy.compare(temp,r[mid])<0)
hi = mid - 1;
else lo = mid + 1;
}
for (int j=i-1;j>hi;j--) r[j+1] = r[j]; //移动元素
r[hi+1] = temp; //插入元素
}//for
}
复杂度分析
折半插入排序所需的辅助空间与直接插入排序相同,从时间上比较,折半插入排序仅减少了元素的比较次数,但是并没有减少元素的移动次数,因此折半插入排序的时间复杂度仍为O(n²)。
2.3希尔排序
希尔排序又称为“缩小增量排序”,它也是一种属于插入排序类的排序方法,是一种对直接插入排序的改进,但在时间效率上却有较大的改进。
基本思想
首先将待排序的元素分为多个子序列,使得每个子序列的元素个数相对较少,对各个子序列分别进行直接插入排序,待整个待排序序列“基本有序”后,再对所有元素进行一次直接插入排序。
根据上述排序思想,下面我们给出希尔排序的排序过程:
⑴ 选择一个步长序列t1,t2,…,tk,其中ti>tj(i<j),tk=1;
⑵ 按步长序列个数k,对待排序元素序列进行k趟排序;
⑶ 每趟排序,根据对应的步长ti,将待排序列分割成ti个子序列,分别对各子序列进行直接插入排序。
当步长因子为1 时,所有元素作为一个序列来处理,其长度为n。
例子:
以关键字序列{ 26 , 53 , 67 , 48 , 57 , 13 , 48, 32 , 60 , 50}为例,假设选择的步长序列为{5 , 3 , 1},则希尔排序的过程如图所示。

因为步长序列长度为3,因此对待排序序列一共需要进行3 趟排序。首先,第一趟排序中将关键字序列分成5个子序列{26 , 13},{53 , 48},{67, 32},{48 , 60},{57 , 50},对它们分别进行直接插入排序,结果如图所示。然后,进行第二趟希尔排序,此时步长为3,则将关键字序列分成3 个子序列{13, 48 , 53 , 57},{48 ,50 , 67},{32, 26 , 60},对它们进行直接插入排序后的结果如图所示。最后,对整个序列进行一趟直接插入排序,此时得到一个关键字有序的序列,希尔排序结束。
代码实现:
//希尔排序
public void shellSort(Object[] r, int low, int high, int[] delta){
for (int k=0;k<delta.length;k++)
shellInsert(r, low, high, delta[k]);
}
private void shellInsert(Object[] r, int low, int high, int deltaK){
for (int i=low+deltaK; i<=high; i++)
if (strategy.compare(r[i],r[i-deltaK])<0){
Object temp = r[i];
int j = i-deltaK;
for(; j>=low&&strategy.compare(temp,r[j])<0; j=j-deltaK)
r[j+deltaK] = r[j];
r[j+deltaK] = temp;
}
}
复杂度分析
直观上我们可以预见希尔排序的效率会较直接插入排序要高,然而对希尔排序的时间复杂度分析是一个复杂的问题,因为希尔排序的时间复杂度与步长序列的选取密切相关,如何选择步长序列才能使得希尔排序的时间复杂度达到最佳,这还是一个有待解决的问题。但是,对于希尔排序的研究已经得出许多有趣的局部结论①例如,当步长序列delta[k]=2t-k+1-1时,希尔排序的时间复杂度为Ο(n3/2),其中t为希尔排序的趟数,1≤k≤t≤⎣log (n+1)⎦。实际的应用中,在选择步长序列时应当注意:应使步长序列中的步长值互质,并且最后一个步长值必须等于1。


