排序---->归并排序
归并排序
归并排序是另一类不同的排序方法,这种方法是运用分治法解决问题的典型范例。
基本思想
归并排序的基本思想是基于合并操作,即合并两个已经有序的序列是容易的,不论这两个序列是顺序存储还是链式存储,合并操作都可以在Ο(m+n)时间内完成(假设两个有序表的长度分别为m 和n)。为此,由分治法的一般设计步骤得到归并排序的过程为:
1. 划分:将待排序的序列划分为大小相等(或大致相等)的两个子序列;
2. 治理:当子序列的规模大于1 时,递归排序子序列,如果子序列规模为1则成为有序序列;
3. 组合:将两个有序的子序列合并为一个有序序列。
例子:
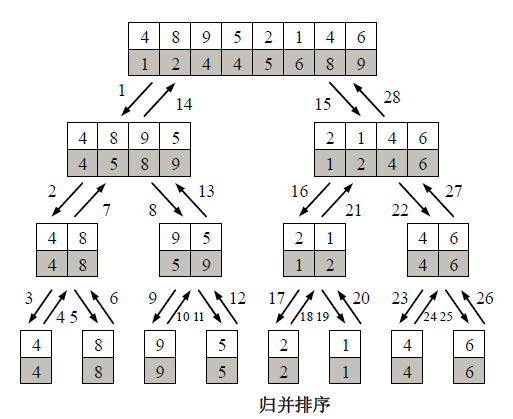
假设待排序序列为{4, 8, 9, 5, 2, 1,4, 6},如图所示,归并排序导致了一系列递归的调用,而这一系列调用过程可以由一个二叉树来表示。树中每个结点由两个序列组成,上端为该结点所表示的递归调用的输入,而下端为相应递归调用的输出。树中的边用表示递归调用方向的两条边取代,边上的序号表示各个递归调用发生的次序。
代码实现
归并排序中一个核心的操作是将一个序列中前后两个相邻的子序列合并为一个有序序列,
输入:数据元素数组a,a 待合并的两个有序区间[p..q]以及[q+1..r]
输出:将两个有序区间合并为一个有序区间
private void merge(Object[] a, int p, int q, int r){
Object[] b = new Object[r-p+1];
int s = p;
int t = q+1;
int k = 0;
while (s<=q&&t<=r)
if (strategy.compare(a[s],a[t])<0)
b[k++] = a[s++];
else
b[k++] = a[t++];
while (s<=q) b[k++] = a[s++];
while (t<=r) b[k++] = a[t++];
for (int i=0; i<b.length; i++)
a[p+i] = b[i];
}
归并排序算法
//归并排序
public void mergeSort(Object[] r, int low, int high){
if (low<high){
mergeSort(r,low,(high+low)/2);
mergeSort(r,(high+low)/2+1,high);
merge(r,low,(high+low)/2,high);
}
}
效率分析
空间效率:在归并排序中,为了将子序列合并需要使用额外的存储空间,这个辅助存储空间的最大值不超过n,因此归并算法的空间复杂度为Θ(n)。
时间效率:归并算法是一个典型的分治算法,因此,它的时间复杂度可以用MasterMethod 来求解。通过对算法的分析我们写出算法时间复杂度的递推关系式:
T(n) = 2T(n/2) + Θ(n)
该递推式满足Master Method 的第二种情况,因此T(n) = Ο(nlog n)。
与快速排序和对排序相比,归并排序的优点是它是一种稳定的排序方法。上述算法实现是归并排序的递归形式,这种形式简洁易懂,然而实用性较差,归并排序还可以按照自底向上的方式给出其他实现。
public void bottomUpSort(Object[] r, int low, int high){
int t= 1;
while (t<high-low+1){
int s = t;
t = 2 * s;
int i = low-1;
while (i+t<=high){
merge(r,i+1,i+s,i+t);
i = i + t;
}
if (i+s<high) merge(r,i+1,i+s,high);
}
}


