排序---->交换排序
交换排序
交换类排序主要是通过两两比较待排元素的关键字,若发现与排序要求相逆,则“交换”之。在这类排序方法中最常见的是冒泡排序和快速排序,其中快速排序是一种在实际应用中具有很好表现的算法。
3.1冒泡排序
基本思想
冒泡排序(BubbleSort)的基本概念是:依次比较相邻的两个数,将小数放在前面,大数放在后面。即在第一趟:首先比较第1个和第2个数,将小数放前,大数放后。然后比较第2个数和第3个数,将小数放前,大数放后,如此继续,直至比较最后两个数,将小数放前,大数放后。至此第一趟结束,将最大的数放到了最后。在第二趟:仍从第一对数开始比较(因为可能由于第2个数和第3个数的交换,使得第1个数不再小于第2个数),将小数放前,大数放后,一直比较到倒数第二个数(倒数第一的位置上已经是最大的),第二趟结束,在倒数第二的位置上得到一个新的最大数(其实在整个数列中是第二大的数)。如此下去,重复以上过程,直至某一趟的交换顺序为0,最终完成排序。
举例:
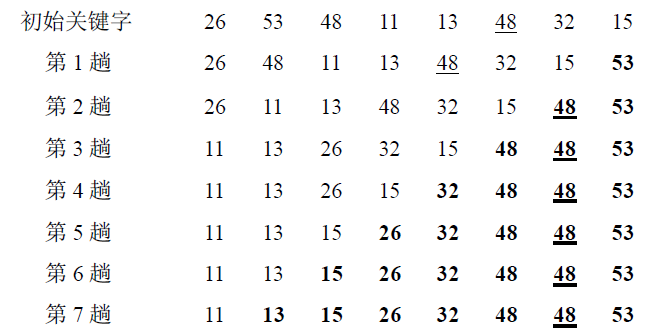
代码实现
代码实现1:
//冒泡排序
public void bubbleSort(Object[] r, int low, int high){
int n = high - low + 1;
for (int i=1;i<n;i++)
for (int j=low;j<=high-i;j++)
if (strategy.compare(r[j],r[j+1])>0)
{
Object temp = r[j];
r[j] = r[j+1];
r[j+1] = temp;
}
}
代码实现2
import junit.framework.TestCase;
public class BubbleSort extends TestCase {
public void sort(Integer a[]) {
boolean exchange = false; // 某一趟的交换次数为0
for (int i = a.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (a[j + 1] < a[j]) {
exchange = true;
Integer temp = a[j + 1];
a[j + 1] = a[j];
a[j] = temp;
}
}
if (!exchange) { //如果本趟排序次数为0,表示排序次数为0
break;
}
}
}
public void test() {
Integer a[] = {10,-3,5,34,-34,5,0,9 };
sort(a);
for (int i = 0; i < a.length; i++) {
System.out.print(a[i] + "、");
}
}
}
效率分析
空间效率:仅使用一个辅存单元。
时间效率:假设待排序的元素个数为n,则总共要进行n-1趟排序,对j个元素的子序列进行一趟起泡排序需要进行j-1 次关键字比较。由此,起泡排序的总比较次数为
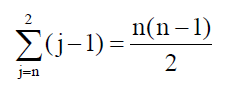 因此,起泡排序的时间复杂度为Ο(n2)。
因此,起泡排序的时间复杂度为Ο(n2)。
3.2快速排序
基本思想
快速排序是将分治法运用到排序问题中的一个典型例子,快速排序的基本思想是:通过一个枢轴(pivot)元素将n个元素的序列分为左、右两个子序列Ll 和Lr,其中子序列Ll中的元素均比枢轴元素小,而子序列Lr 中的元素均比枢轴元素大,然后对左、右子序列分别进行快速排序,在将左、右子序列排好序后,则整个序列有序,而对左右子序列的排序过程直到子序列中只包含一个元素时结束,此时左、右子序列由于只包含一个元素则自然有序。
用分治法的三个步骤来描述快速排序的过程如下:
-
划分步骤:通过枢轴元素 x 将序列一分为二,且左子序列的元素均小于x,右子序列的元素均大于x;
-
治理步骤:递归的对左、右子序列排序;
-
组合步骤:无
从上面快速排序算法的描述中我们看到,快速排序算法的实现依赖于按照枢轴元素x对待排序序列进行划分的过程。
对待排序序列进行划分的做法是:使用两个指针low 和high 分别指向待划分序列r的范围,取low所指元素为枢轴,即pivot = r[low]。划分首先从high 所指位置的元素起向前逐一搜索到第一个比pivot 小的元素,并将其设置到low 所指的位置;然后从low 所指位置的元素起向后逐一搜索到第一个比pivot 大的元素,并将其设置到high 所指的位置;不断重复上述两步直到low = high 为止,最后将pivot 设置到low 与high 共同指向的位置。使用上述划分方法即可将待排序序列按枢轴元素pivot 分成两个子序列,当然pivot 的选择不一定必须是r[low],而可以是r[low..high]之间的任何数据元素。
举例:

代码实现
代码实现1:
//快速排序
public void quickSort(Object[] r, int low, int high){
if (low<high){
int pa = partition(r,low,high);
quickSort(r,low,pa-1);
quickSort(r,pa+1,high);
}
}
private int partition(Object[] r, int low, int high){
Object pivot = r[low];
while (low<high){
while(low<high&&strategy.compare(r[high],pivot)>=0) high--;
r[low] = r[high];
while(low<high&&strategy.compare(r[low],pivot)<=0) low++;
r[high] = r[low];
}
r[low] = pivot;
return low;
}
代码实现2
public class QuickSort {
public static void sort(Comparable[] data, int low, int high) {
// 枢纽元,一般以第一个元素为基准进行划分
int i = low;
int j = high;
if (low < high) {
// 从数组两端交替地向中间扫描
Comparable pivotKey = data[low];
// 进行扫描的指针i,j;i从左边开始,j从右边开始
while (i < j) {
while (i < j && data[j].compareTo(pivotKey) > 0) {
j--;
}// end while
if (i < j) {
// 比枢纽元素小的移动到左边
data[i] = data[j];
i++;
}// end if
while (i < j && data[i].compareTo(pivotKey) < 0) {
i++;
}// end while
if (i < j) {
// 比枢纽元素大的移动到右边
data[j] = data[i];
j--;
}// end if
}// end while
// 枢纽元素移动到正确位置
data[i] = pivotKey;
// 前半个子表递归排序
sort(data, low, i - 1);
// 后半个子表递归排序
sort(data, i + 1, high);
}// end if
}// end sort
public static void main(String[] args) {
Comparable[] c = { 49 ,38, 65, 97, 76, 13, 27 };
sort(c, 0, c.length - 1);
for (Comparable data : c) {
System.out.println(data);
}
}
}
效率分析
时间效率:快速排序算法的运行时间依赖于划分是否平衡,即根据枢轴元素pivot将序列划分为两个子序列中的元素个数,而划分是否平衡又依赖于所使用的枢轴元素。下面我们在不同的情况下来分析快速排序的渐进时间复杂度。
快速排序的最坏情况是每次进行划分时,在所得到的两个子序列中有一个子序列为空。此时,算法的时间复杂度T(n) = Tp(n)+T(n-1),其中Tp(n)是对具有n个元素的序列进行划分所需的时间,由以上划分算法的过程可以得到Tp(n) = Θ(n)。由此,T(n) =Θ(n)+T(n-1) =Θ(n²)。在快速排序过程中,如果总是选择r[low]作为枢轴元素,则在待排序序列本身已经有序或逆向有序时,快速排序的时间复杂度为Ο(n²),而在有序时插入排序的时间复杂度为Ο(n)。
快速排序的最好情况是在每次划分时,都将序列一分为二,正好在序列中间将序列分成长度相等的两个子序列。此时,算法的时间复杂度T(n) = Tp(n) +2T(n/2),由于Tp(n) = Θ(n),所以T(n) =2T(n/2)+Θ(n),由master method知道T(n)=Θ(nlog n)。
平均情况下,快速排序的时间复杂度T(n) = knlog n,其中k 为某个常数,经验证明,在所有同数量级的排序方法中,快速排序的常数因子k是最小的。因此就平均时间而言,快速排序被认为是目前最好的一种内部排序方法。
快速排序的平均性能最好,但是,若待排序序列初始时已按关键字有序或基本有序,则快速排序蜕化为起泡排序,其时间复杂度为Ο(n2)。为改进之,可以采取随机选择枢轴元素pivot的方法,具体做法是,在待划分的序列中随机选择一个元素然后与r[low]交换,再将r[low]作为枢轴元素,作如此改进之后将极大改进快速排序在序列有序或基本有序时的性能,在待排序元素个数n较大时,其运行过程中出现最坏情况的可能性可以认为不存在。
空间效率:虽然从时间上看快速排序的效率优于前述算法,然而从空间上看,在前面讨论的算法中都只需要一个辅助空间,而快速排序需要一个堆栈来实现递归。若每次划分都将序列均匀分割为长度相近的两个子序列,则堆栈的最大深度为log n,但是,在最坏的情况下,堆栈的最大深度为n。


