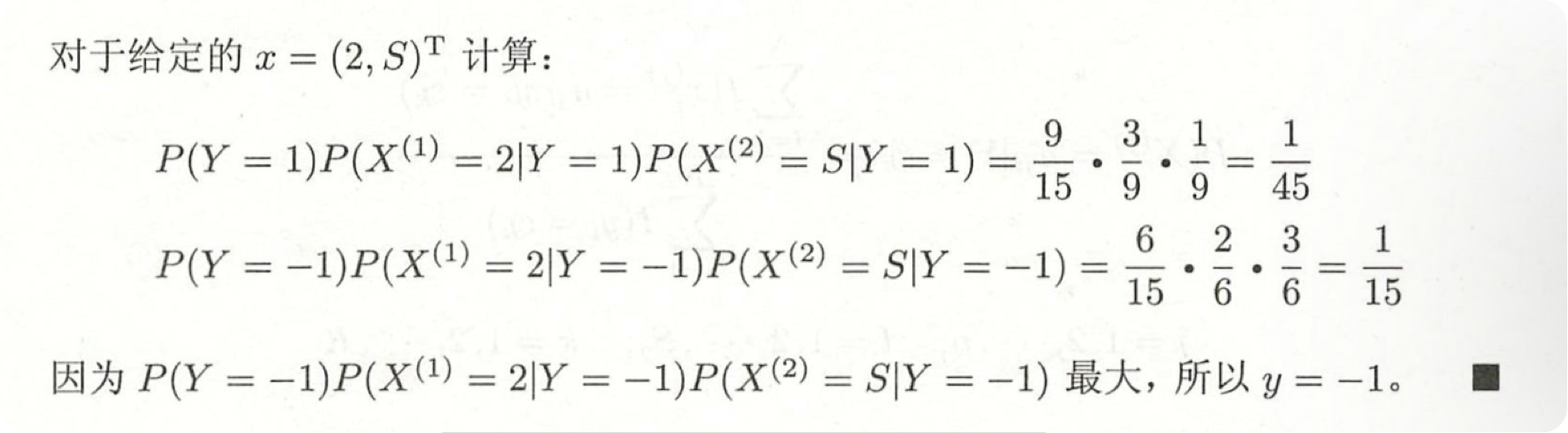朴素贝叶斯 Naive Bayesian Model
描述
贝叶斯分类算法,顾名思义是用来解决分类问题的。
从数学角度来说,分类问题可做如下定义:已知集合\(C=y_1,y_2,\cdots,y_n\)和\(I=x_1,x_2,\cdots,x_n\),确定映射规则\(y = f()\),使得任意\(x_i \in I\)有且仅有一个\(y_i \in C\),使得\(y_i \in f(x_i)\)成立。其中\(C\)叫做类别集合,其中每一个元素是一个类别,\(I\)叫做特征集合,其中每一个元素是一个待分类项,\(f\)叫做分类器。分类算法的任务就是构造分类器\(f\)。
基础回顾
先验概率:通过经验来判断事情发生的概率
比如发病率是万分之一
后验概率:事情发生之后,推测原因的概率
比如已经患有某疾病,有A,B,C三种原因,A导致该疾病的概率就是后验概率(也是条件概率的一种)
条件概率:事件B发生的情况下事件A发生的概率,记作$P(A|B)
比如原因A的条件下患有某疾病的概率就是条件概率
核心思想
贝叶斯定理
\[p(B|A)= \frac {p(A|B)p(B)} {p(A)}
\]
在分类问题中就是
\[p(类别|特征)= \frac {p(特征|类别)p(类别)} {p(特征)}
\]
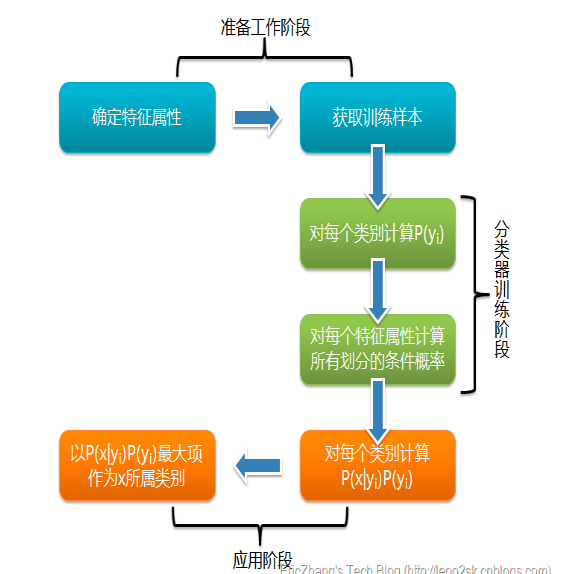
算法描述:
- 设\(x={a_1,\cdots,a_m}\)为一个待分类项,\(a_i\)为\(x\)的一个特征属性
- 有待分类集合\(C={y_1,\cdots,y_n}\)
- 计算\(P(y_1|x),P(y_2|x),\cdots,P(y_n|x)\)
具体就是统计得到在各类别下各个特征的条件概率,即
\[P(a_1|y_1),\cdots,(a_m|y_1);\cdots;P(a_1|y_n),\cdots,(a_m|y_n)
\]
\[P(y_i|x)= \frac {P(x|y_i)P(y_i)} {P(x)}
\]
因为分母是给定的特征,对于各个类别来说均一样,看作常数,所以最大化分子即可
\[P(x|y_i)P(y_i)=P(a_1|y_i)P(a_2|y_i)\cdots P(a_m|y_i)P(y_i)=P(y_i)\prod_{j=1}^mP(a_j|y_i)
\]
- \(P(y_k|x)=\max\{P(y_1|x),P(y_2|x),\cdots,P(y_n|x)\}\),则\(x \in y_k\)
所以朴素贝叶斯的算法就是
\[y=\max P(Y=c_k)\prod_{j=1}^mP(X^{(j)}=x^{(j)}|Y=c_k)
\]
为什么“朴素”
朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了,这也就是为什么朴素贝叶斯分类有“朴素”的来源
但是为什么需要假设特征之间相互独立呢?
如果不相互独立,计算概率就不能分开连乘,而且计算联合概率分布非常麻烦,四个特征的联合概率分布总共是4维空间
例子