凸函数 Convex Function

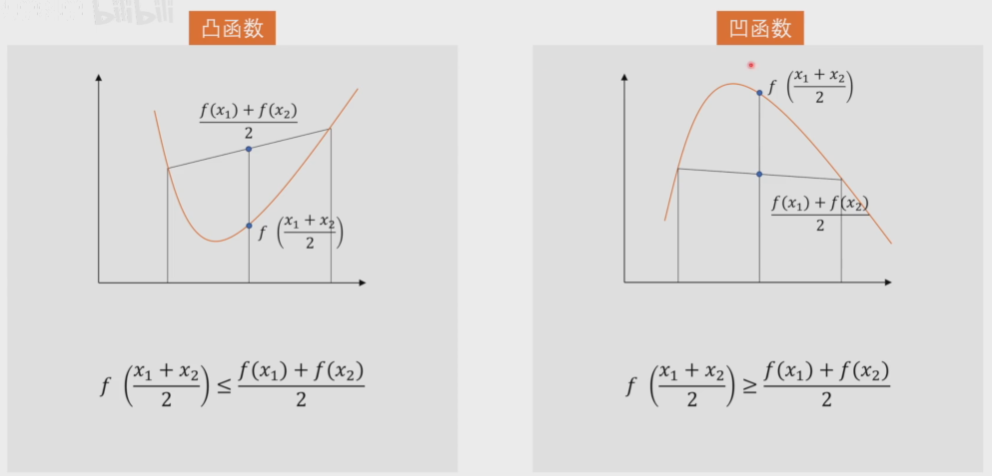
凸函数定义

\[\forall x_1,x_2 \in D(f), 0\le\theta\le1\\ f(\theta\cdot x_1+(1-\theta)\cdot x_2) \le f(\theta\cdot x_1)+ f((1-\theta)\cdot x_2) \]

同理，凹函数则是\(\ge\)。凸函数和凹函数均为凸集
凸函数有最小值，凹函数有最大值，把凹函数加个负号也就转换成了凸函数
上述凸函数和凹函数都属于凸问题，与非凸问题相对

凸函数的一阶特征 First Order Condition for Convexity

设\(S \in R^n\)为非空开凸集，\(f\)满足一阶连续可导且为\(S\)上的凸函数,则满足

\[\forall x,y \in S, \ f(y) \ge f(x)+\nabla f(x)^T(y-x) \]

从图像上直观来看

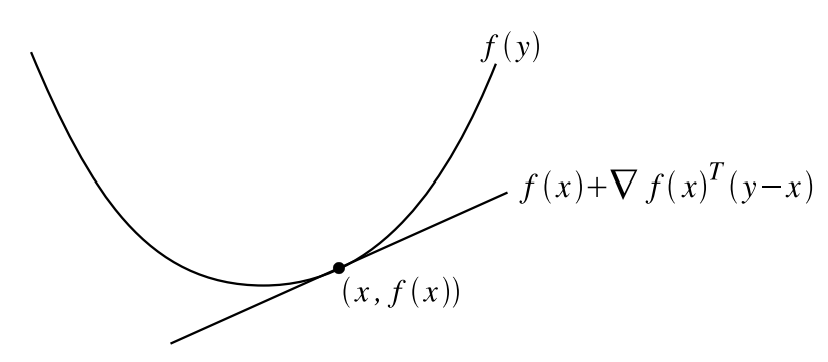
这个函数上的任意一点，函数的值都大于或者等于函数在这点的一阶近似（first-order approximation）

证明

凸函数的二阶条件

\(f:R^n\rightarrow R\)二阶可微,则\(f\)为凸函数 \(\Longleftrightarrow\) \(domf\)为凸集，且\(\nabla f^2(x) \ge 0, \quad \forall x \in {\rm dom}f\)
也就是说二阶Hessian是半正定的