正则化 Regularization
什么是正则化
凡是减少泛化误差(而不是训练误差)的方法都可以称作正则化
换句话说,也就是减小过拟合的方法
范数 Norm
L1范数:\(||W||_1={|w_1|+|w_2|+\cdots+|w_n|}\)
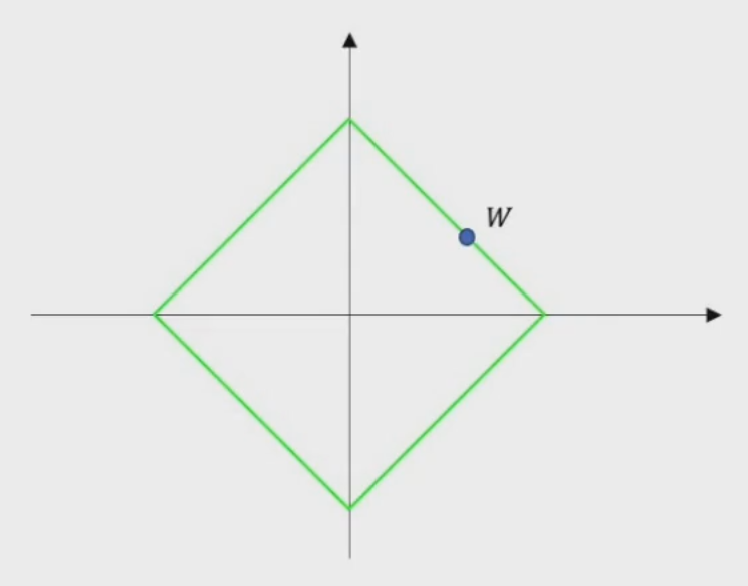
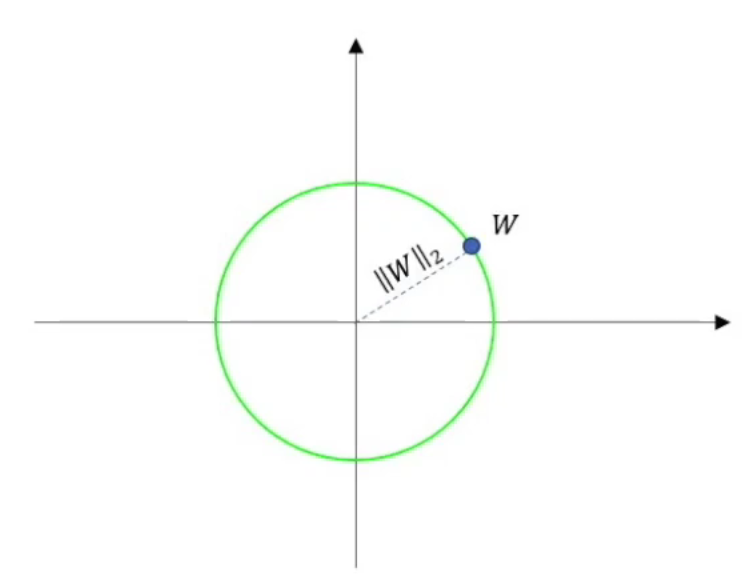
把权重\(W\)看作空间中的向量,如果\(W\)到原点的距离是欧式距离的话,那么这个范数就是L2范数:\(||W||_2=\sqrt {|w_1|^2+|w_2|^2+\cdots+|w_n|^2}\)
其他范数
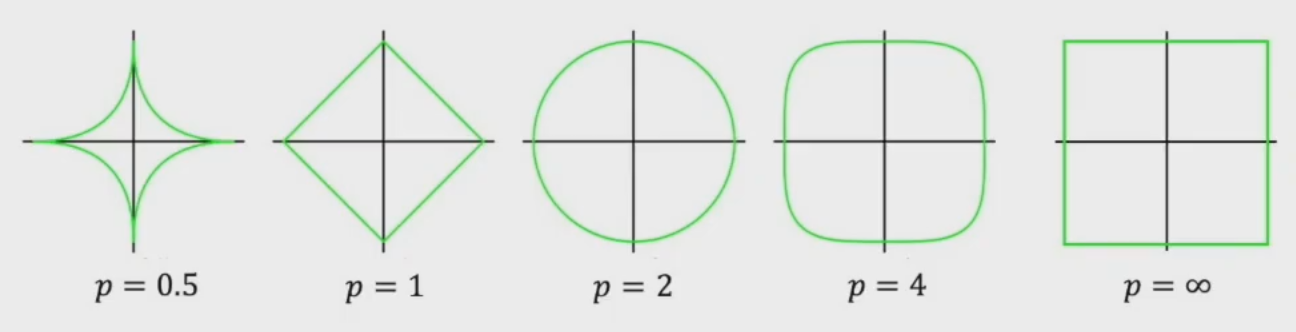
从图中可以看出,在\(p\ge 1\)时构成的集合才是个凸集
为何要正则化
从三个不同的角度来理解正则化的作用
拉格朗日乘数法
训练神经网络时,权重的初始值会影响最后的结果,经过不同的模型,权重的结果或大或小,这个结果在训练集上不会有什么影响,但如果输入新的数据集,这个影响就显现出来了。因为如果权重过大,误差和噪声也会被放大。为了解决这个问题,我们使用正则化来控制参数。
从拉格朗日乘数法的角度来理解,就是人为的给参数范围加一个约束(可行域),在可行域范围之内求最值。如果超出可行域范围,即使损失函数取值再小也不被采纳
这里只用约束\(W\)即可,因为\(W\)是最后决定曲线形状的,而\(b\)只是一个偏置
因为是对于\(W\)找最值,只要算出\(W\)即可,所以一般的正则化都是如下公式
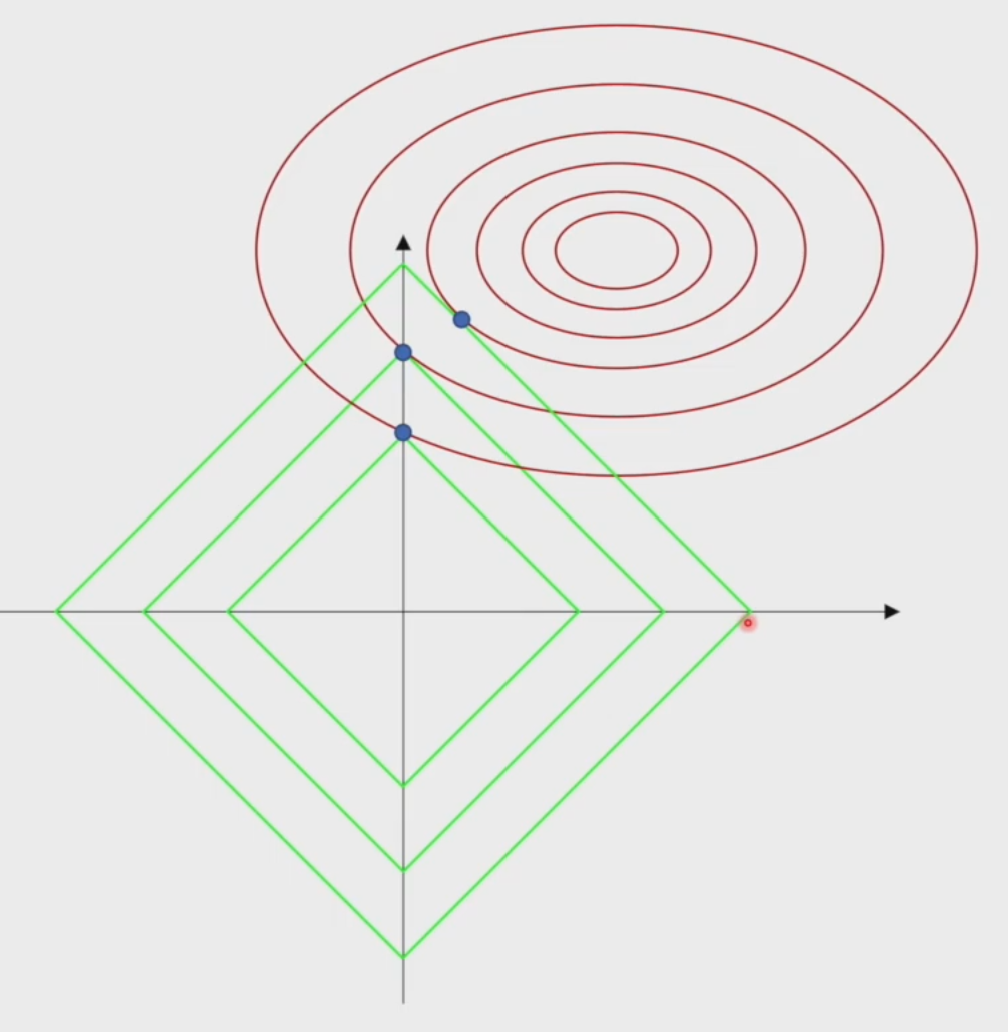
从二维图像上直观感受一下

L1正则化的稀疏性:可以调整\(\lambda\)使得某些\(w_i\)有值,也就是某些特征起作用,从图像上看就是在某些数轴上有值
权重衰减 Weight Decay
加了正则化项之后损失函数为:其中\(\frac 1 2\)是为了求导好计算
权重更新的计算为
从这个计算可以看出跟原始的梯度下降算法(\(W\)减去学习率乘梯度)不同,这里的\(W\)先乘了一个大于0小于1的数,也就相当于在梯度更新之前权重\(W\)先相对于之前衰减了一部分
类比一下,这就相当于给权重的更新加了个毒圈,以前权重可以满地图随便跑,但是增加了毒圈之后只能在一定范围内活动,并且每走一步毒圈都会缩小一点
再从图像上理解一下,惩罚之后的\(W\)变小了,那么模型的函数泰勒展开后的那些coefficient(也就是k阶导数)也变小了,那么函数的弯弯绕绕也不会那么精确而导致过拟合,如下图
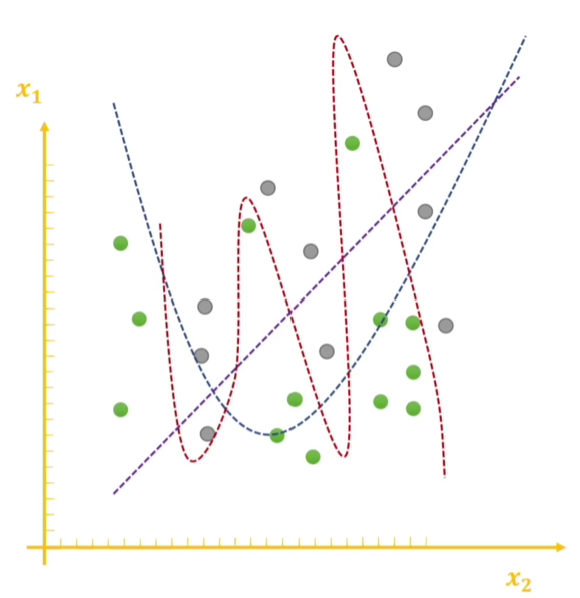
但是要注意:正则化可不完全等价于权重衰减
具体可看这篇论文:DECOUPLED WEIGHT DECAY REGULARIZATION
L2 regularization and weight decay regularization are equivalent for standard stochastic gradient descent (when rescaled by the learning rate), but as we demonstrate this is not the case for adaptive gradient algorithms, such as Adam.
贝叶斯概率
正则化与原解的关系
首先将原损失函数进行二阶泰勒展开
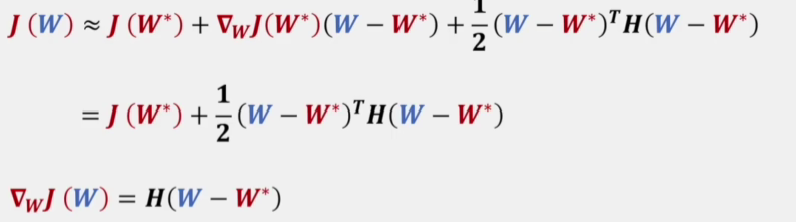
再计算加上正则化项后的梯度
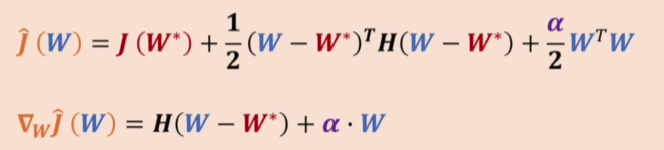
从而可以计算出原解(红色)和正则化后解(橘色)的关系
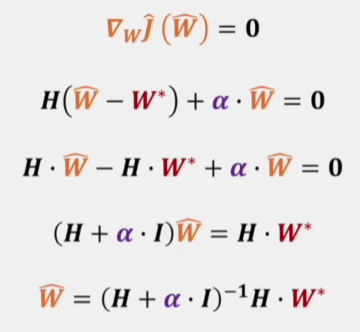
再利用Hessian矩阵的性质对式子进行一下变形
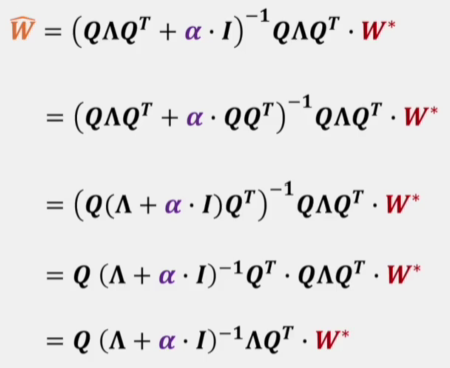
最后得到
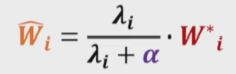
所以L2正则化就是对原损失函数极值点\(W\)进行缩放,缩放的比例取决于\(\alpha\)
而L1正则化要麻烦许多,花书上假设Hessian矩阵是对角的来简化问题,即\(H={\rm diag}([H_{1,1},\cdots,H_{n,n}])\)
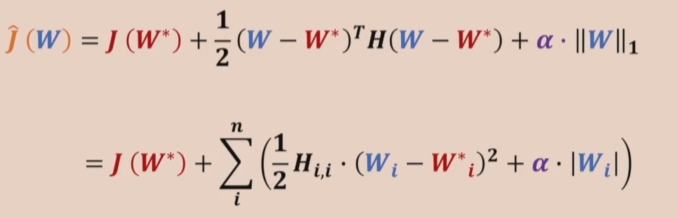


这也就解释了为什么L1正则化带来的稀疏性,因为落在这个范围之内的\(W\)都会变成0
Reference
从拉格朗日乘数法角度进行理解
为什么又叫权重衰减?到底哪里衰减了
花书教我明白伤痛——L1正则
拉格朗日乘数法;权重衰减;贝叶斯概率


