Contrastive Predictive Coding(CPC)
Representation Learning with Contrastive Predictive Coding(CPC)
为什么叫Contrastive Predictive Coding
也就是说当前输入\(x_i\)和经过encoder学得的latent vector \(y_i\)配对,送入discriminator告诉ta这是正样本
Motivation
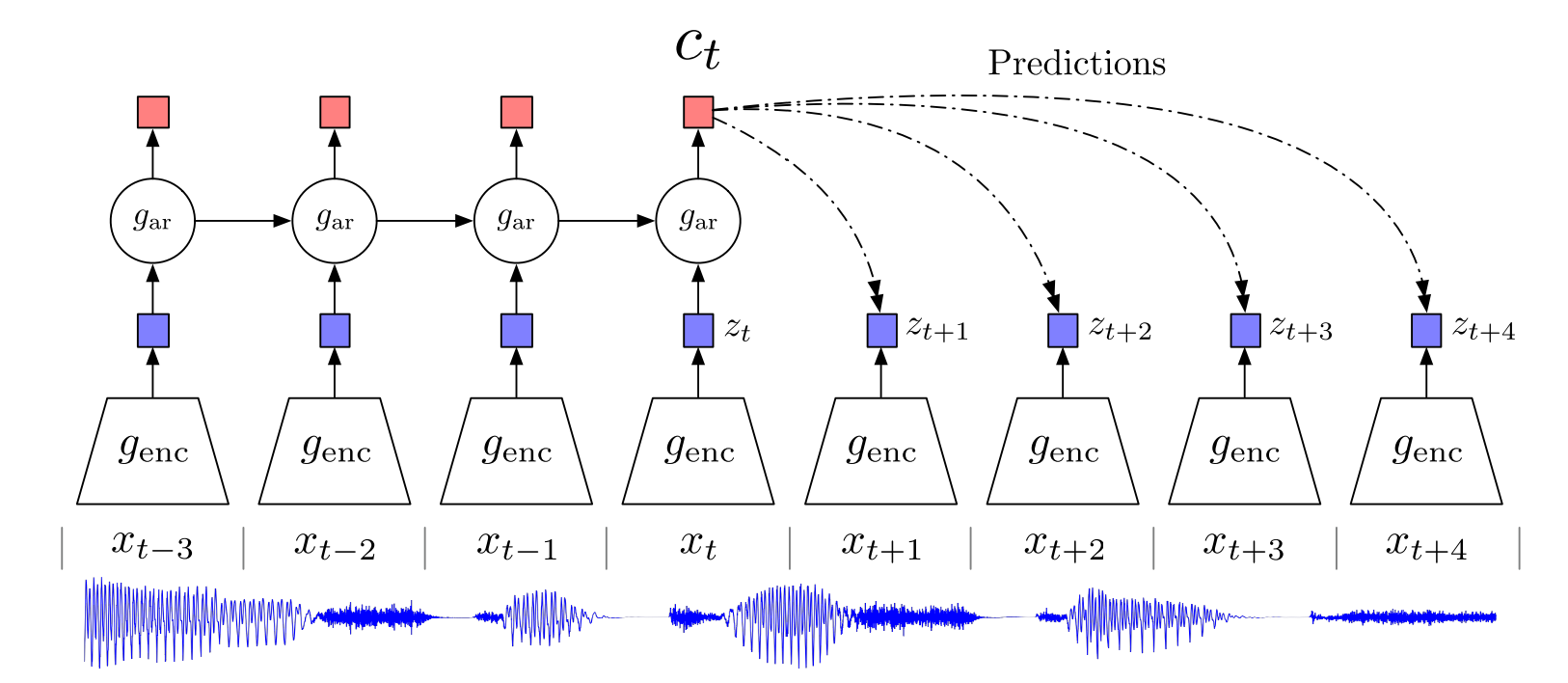
下图中\(g_{enc}\)是nonlinear encoder,\(z_t\)是编码后的特征latent vector
\(g_{ar}\) is an autoregressive model that summarizes all \(z \le t\) in the latent space and produces a context latent representation\(c_t=g_{ar}(z \le t)\)
也就是说将\(z_t\)以及之前所有时刻的相关信息输入到一个自回归模型中,生成当前时刻的上下文表示\(c_t\)
Predict the future->Good Representation->Mutual Information
也就是说想要得到好的预测我们要最大化input \(x_t\)和context \(c_t\)的互信息(Mutual Information),即尽可能多的用\(c_t\)去表达原始信号\(x\)
所以论文不采用生成模型\(p(x_{t+k}|c)\)进行预测,而是最大化mutual information使得预测的\(\tilde z_{t+k}\)与真实的\(z_{t+k}\)尽可能接近
但是\(p(x,c)\)无法直接获得,所以要提出一个模型去近似未来真实数据与随机采样数据的概率之比
a simple log-bilinear model
\(W\)的下标\(k\)是指预测未来不同时刻时要用到不同的参数,\(z_{t+k}^T\)是真实值,用向量内积来衡量相似度
Method
InfoNCE Loss
一个batch中的N个随机样本包括
- 一个正样本从\(p(x_{t+k}|c_t)\)中采样:来自与当前的上下文\(c_t\)相隔\(k\)个步长的样本
- 剩余\(N-1\)个负样本从与\(c_t\)无关的\(p(x_{t+k})\)分布中取得:来自从序列随机选取的样本
\((x_{t+k},c_t)\)可以看成正样本对,\((x_j,c_t)\)可以看成负样本对
The loss is the categorical cross-entropy of classifying the positive sample correctly.
InfoNCE Loss定义如下,相当于一个多分类交叉熵损失
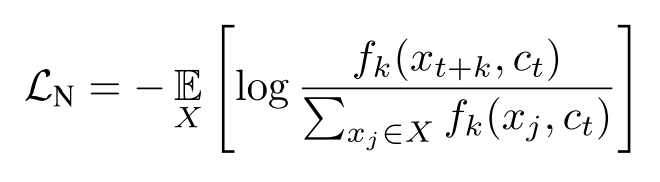
优化该损失函数,应使分子尽可能大,也就是正样本对之间的互信息更大,负样本对之间的互信息更小。优化该损失,实际上就是最大化\(x_{t+k}\)和\(c_t\)间的互信息
这里有个问题,负样本是随机采样的,那么负样本中也可能有与要预测的结果相关的样本信息
问题解决:在具体实践时,常常在对一个batch进行训练时,把当前sample的\((x_{t+k}^i,c_t^i)\)当作正样本对,把batch中其他samples和当前sample的预测值配对\((x_{t+k}^j,c_t^i)\)来计算
Mutual Information Estimation
上述损失函数的optimal情况:假设\(x_i\)是\(c_t\)的预测结果,即正样本,那么\(x_i\)从条件分布\(p(x_{t+k}|c_t)\)中采样出来的概率如下,也就是f的最优解
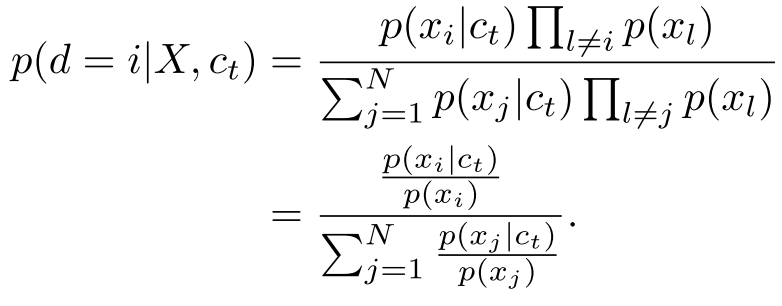
可以看出\(f_k(x_{t+k},c_t)\)确实与\(\displaystyle \frac {p(x_{t+k}|c_t)} {p(x_{t+k})}\)成比例
于是把\(\displaystyle \frac {p(x_{t+k}|c_t)} {p(x_{t+k})}\)带入到InfoNCE Loss中
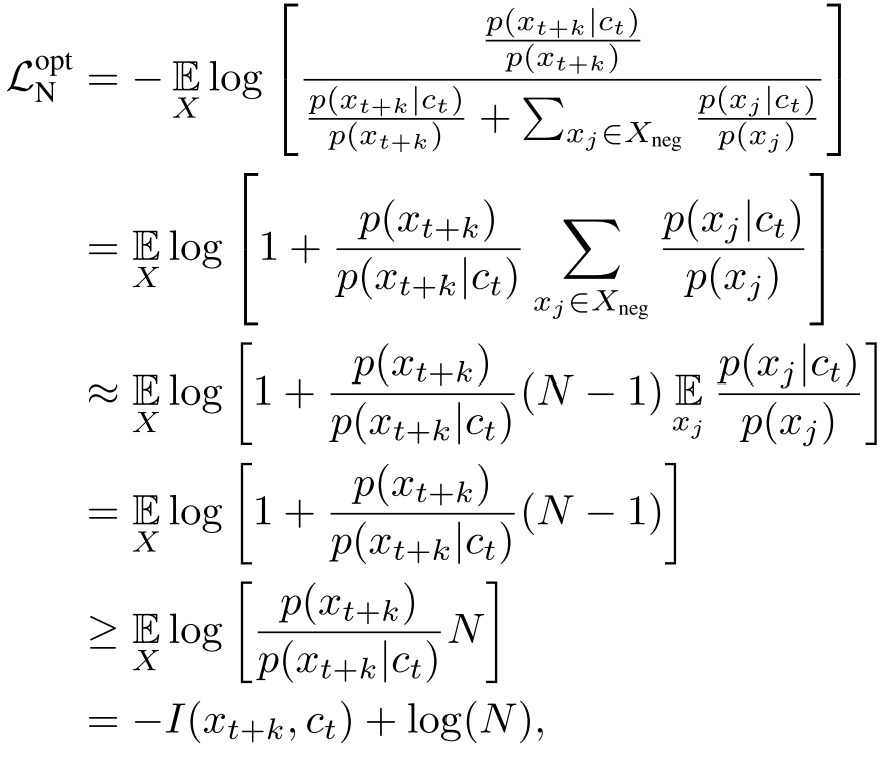
证明了最小化InfoNCE也就是最大化互信息
Experiments
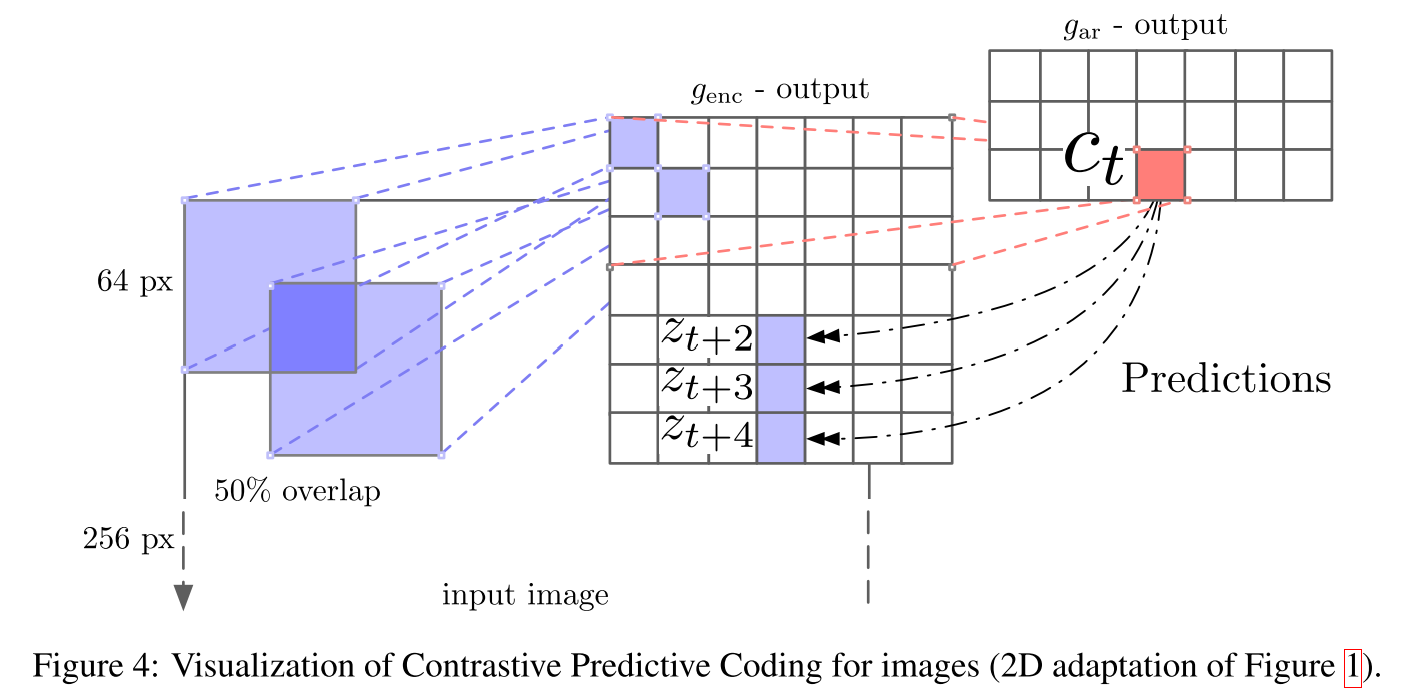
图像分类上的应用,用7x7个64x64大小小的grid在256x256的图上去crop,crop间有50%重叠,每个crop送入encoder(ResNet-101),把前几个patch作为输入,预测后面的patch
参考博客
参考视频


