勒让德变换 Legendre transformation
问题引入
如何将\(f(x,y)\)变换成\(G(u,y)\)
过程推导
\[\begin{align*}
&f(x,y)=f(x_1,\cdots,x_n,y_1,\cdots,y_n)\\
&df=\frac {\partial f} {\partial x_1}dx_i+\cdots+\frac {\partial f} {\partial x_n}dx_n+\frac {\partial f} {\partial y_1}dy_i+\cdots+\frac {\partial f} {\partial y_n}dy_n\\
let \quad &\frac {\partial f} {\partial x_i}=u_i\tag 1\\
&df=\sum_{i=1}^n u_idx_i+\sum_{i=1}^n \frac {\partial f} {\partial y_i}dy_i\\
\because \ &d(ux)=udx+xdu\\
\therefore \ &df=\sum_{i=1}^n d(u_ix_i)-\sum_{i=1}^n x_idu_i+\sum_{i=1}^n \frac {\partial f} {\partial y_i}dy_i\\
&\sum_{i=1}^n x_id_i-\sum_{i=1}^n \frac {\partial f} {\partial y_i}dy_i=d(\sum_{i=1}^n d(u_ix_i)-f(x,y))\tag 2\\
let \quad G(u,y)&=\sum_{i=1}^n d(u_ix_i)-f(x,y)\tag 3\\
&=u^Tx-f(x,y)\\
\end{align*}
\]
对\((3)\)求偏导,再和\((2)\)比较得
\[G(u,y)=
\begin{cases}
& \displaystyle \sum \displaystyle \frac {\partial G} {\partial u_i}du_i-\sum \displaystyle \frac {\partial f} {\partial y_i}dy_i\\
& \displaystyle \sum x_id_i-\sum \displaystyle \frac {\partial f} {\partial y_i}dy_i\\
\end{cases}
\]
纵向比较,再综合前面的\((1)\)得出
\[\begin{cases}
& \displaystyle\frac {\partial G} {\partial u_i}du_i=x_i\\
& \displaystyle\frac {\partial G} {\partial y_i}dy_i = -\frac {\partial f} {\partial y_i}dy_i\\
& \displaystyle\frac {\partial f} {\partial x_i}du_i=u_i\\
\end{cases}
\]
有趣的事情发生了
原函数\(f\)对原变量\(x\)求偏导等于新变量\(u\)
新函数\(G\)对新变量\(u\)求偏导等于原变量\(x\)
新函数\(G\)对不变量\(y\)求偏导等于负的原函数\(f\)对不变量\(y\)求偏导
最后,Legendre变换结果为
\[G(u)=u^Tx-f(x)
\]
几何意义
将函数与切线(超平面)联系起来,引入的新变量\(u=\displaystyle\frac {\partial f} {\partial x}\)就是在\(x\)点处的切平面
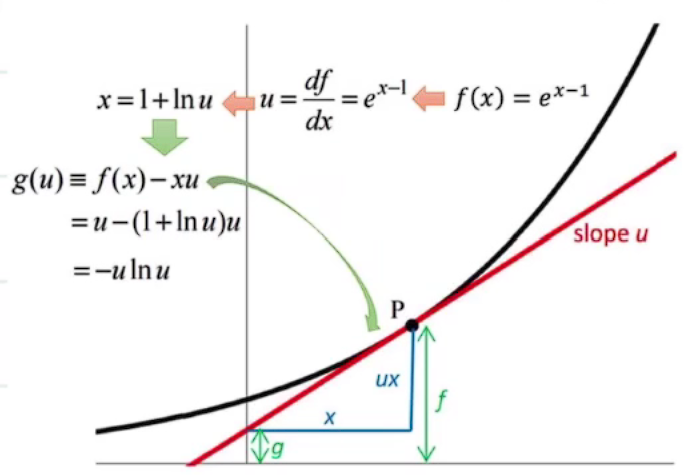
上图减反了,应该是\(ux-f(x)\),在二维空间,\(u\)为函数的斜率(准确来说应该叫梯度),\(u=tan\theta,\ ux\)就是图中蓝色的竖线,最后得到的结果是负的截距(初中知识预警:截距不是距离,有正负之分)
思考
上述过程均是一阶可偏导的,如果遇到非凸函数呢
这个求出来的形式和共轭函数的形式就差一个\(sup\)
其实共轭函数就是对原函数(可能无法求导,非凸函数)求个上界,这个上界是一个凸函数
下一篇:共轭函数

