共轭函数 Conjugate Function
前情提要:勒让德变换
定义
对于原函数\(f(x),x \in D\),其共轭函数为
\[f^*(y)=\sup_{x \in D}(<y,x>-f(x))
\]
其中注意\(<y,x>\)
- 对于标量:\(y \cdot x\)
- 对于向量:\(y^Tx\)
- 对于矩阵:\({\rm tr}(yx)\)
并且\(<y,x>-f(x) < -\infty\),即一定有上界
几何表示
对于共轭函数的每一个自变量\(y=\bar y\),其取值相当于一条直线与原函数之差的最大值
对\(x\)求导得到最大值
\[\frac {\partial (<y,x>-f(x))} {\partial x}=0 \ \Rightarrow \nabla f(x)=y
\]
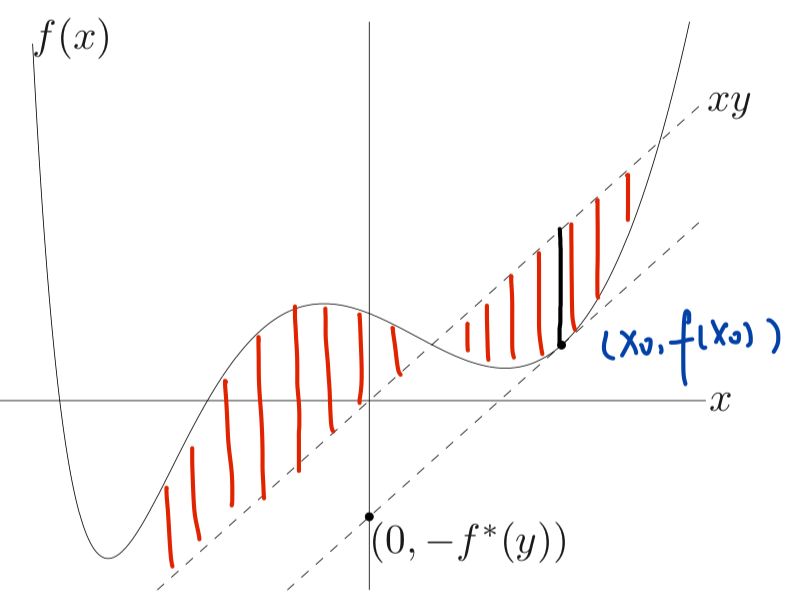
下图二维空间中,红色部分就是\(xy-f(x)\),其中xy是过原点的直线,竖的黑线就是找到的最大差值
将\(xy\)向下平移与\((x_0,f(x_0))\)相切,那么切线可表示为\(h(x)=y(x-x_0)+f(x_0)\)
令\(x=0, \ h(0)=-yx_0+f(x_0)\)
那么就可以发现
\[\begin{align*}
f^*(y)=&\sup_{x \in D}(yx-f(x))\\
=&yx_0-f(x_0)
\end{align*}
\]
那么综合上面的切线可得
\[f^*(y)=-h(0)
\]
也就是说\(f^*(y)\)是切线的负截距
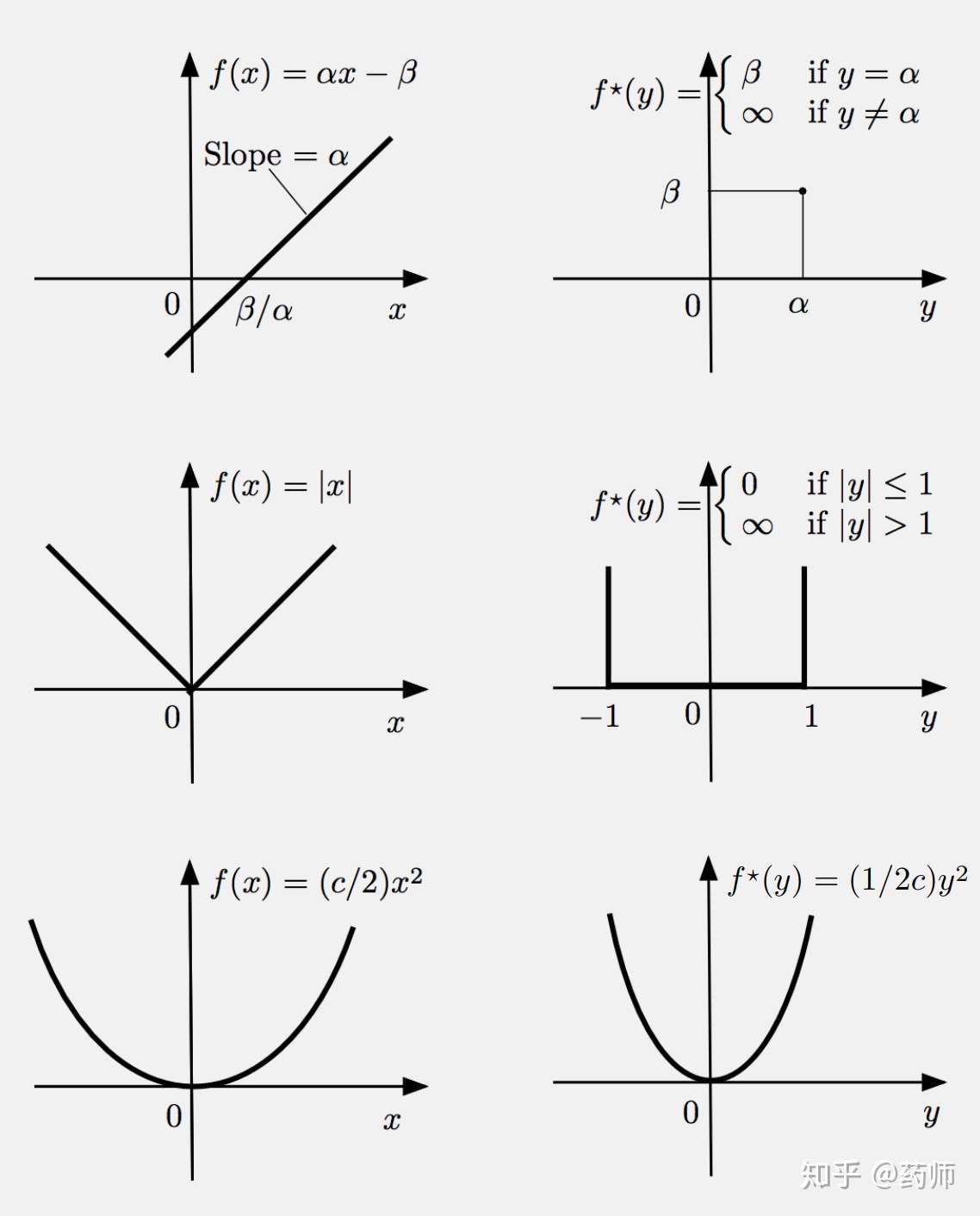
下边给出几个函数与他们的共轭函数
意义
共轭函数的主要作用就是
一个函数即便不是凸函数,但通过共轭法获得一个凸函数,很方便求解全局最优解的问题
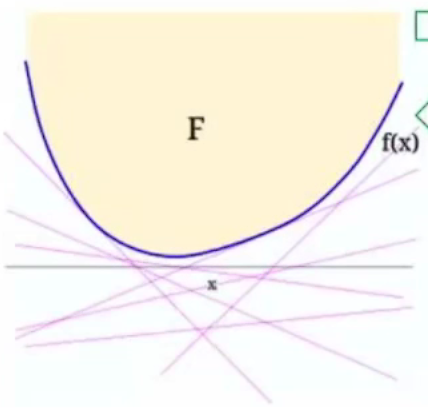
\(f^*(y)\)是对\(y\)的仿射函数,一簇仿射函数的逐点上确界,一定是个凸函数,如下图所示