转置卷积

转置卷积 Transposed Convolution

也叫Fractionally Strided Convolution或Deconvolution
不要被deconvolution这个单词迷惑，转置卷积也是卷积，是将输出特征恢复卷积前的图像尺寸
但注意：不是恢复原始值（因为一般情况下矩阵不可逆，无法等式左右两边同乘矩阵的逆得到原始矩阵)

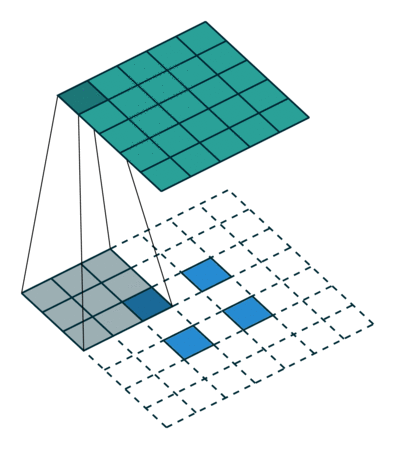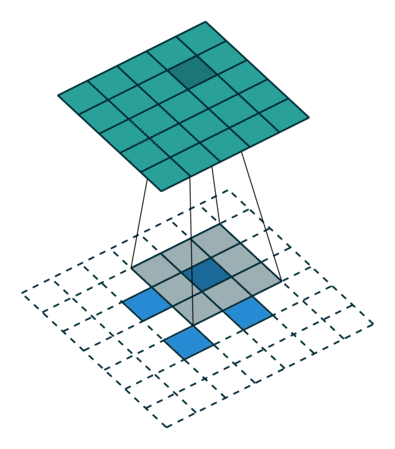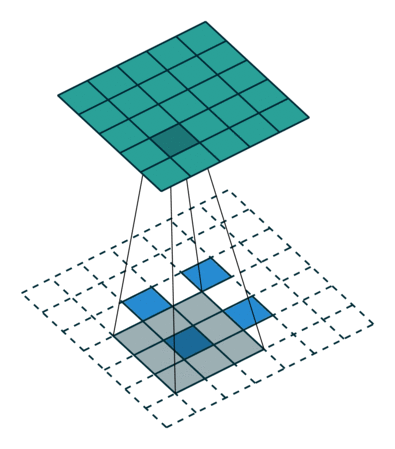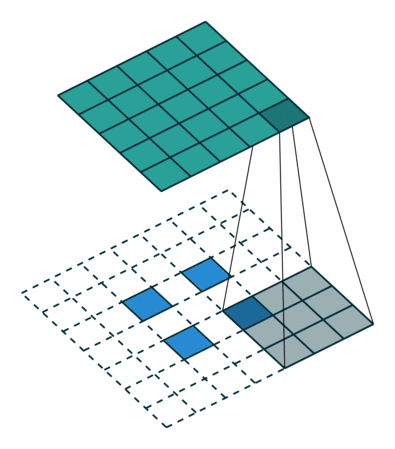
作用：上采样 upsampling

转置卷积的运算步骤

1. 在输入特征图的像素间填充\(stride-1\)行列0
2. 在输入特征图周围填充\(kernal-padding-1\)行列0
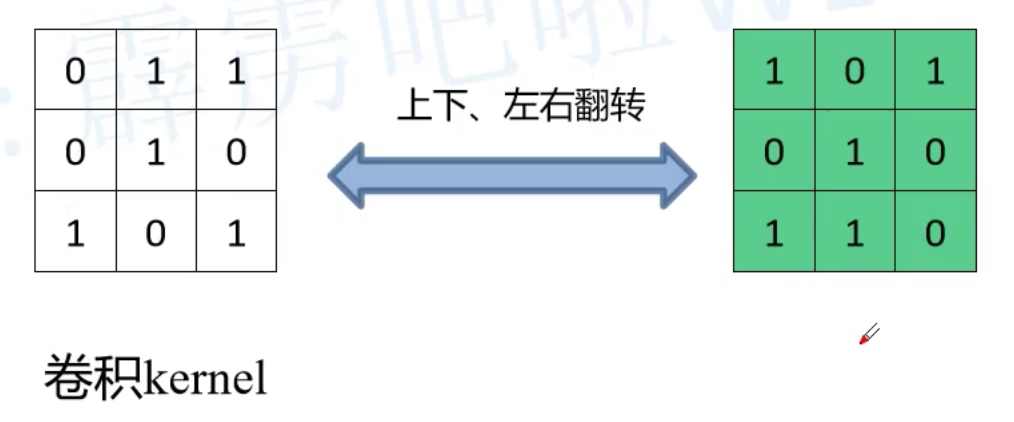
3. 将卷积核参数上下、左右翻转
4. 然后进行正常的卷积操作（padding=0,stride=1) 这里的padding是output_padding

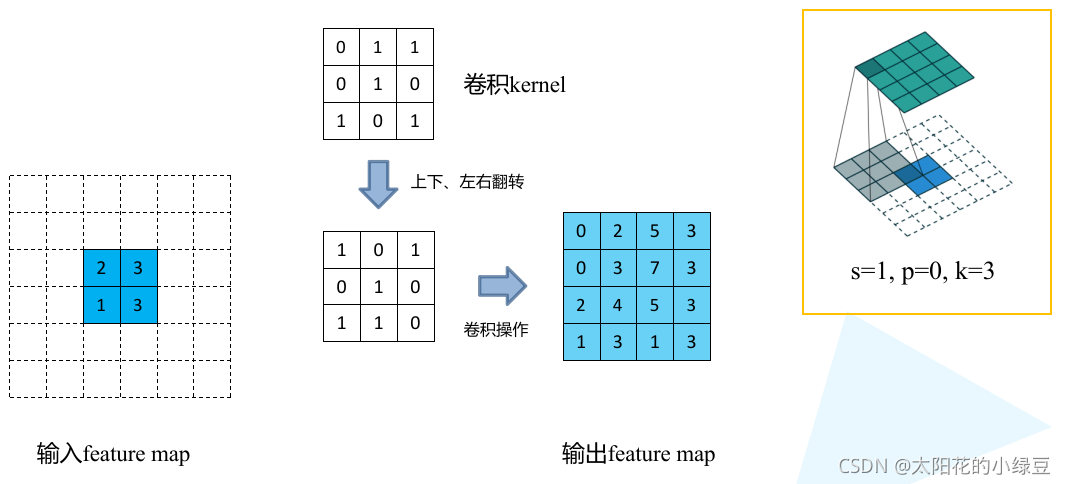
最后输出的特征图尺寸就是卷积操作的逆运算

\[o=(i-1) \cdot s+k-2p \]

torch.nn.ConvTranspose2d参数

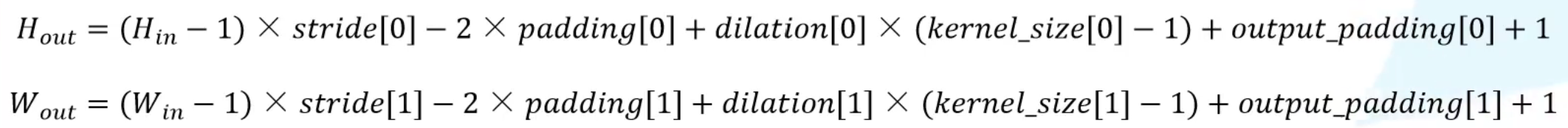
官方给出的公式，dilation是膨胀卷积

转置卷积操作

与之前提到的普通卷积操作一样
转置卷积也是将卷积核变成等效矩阵
因为矩阵不一定有逆，这里用原特征核等效矩阵的逆\(C^T\)代替

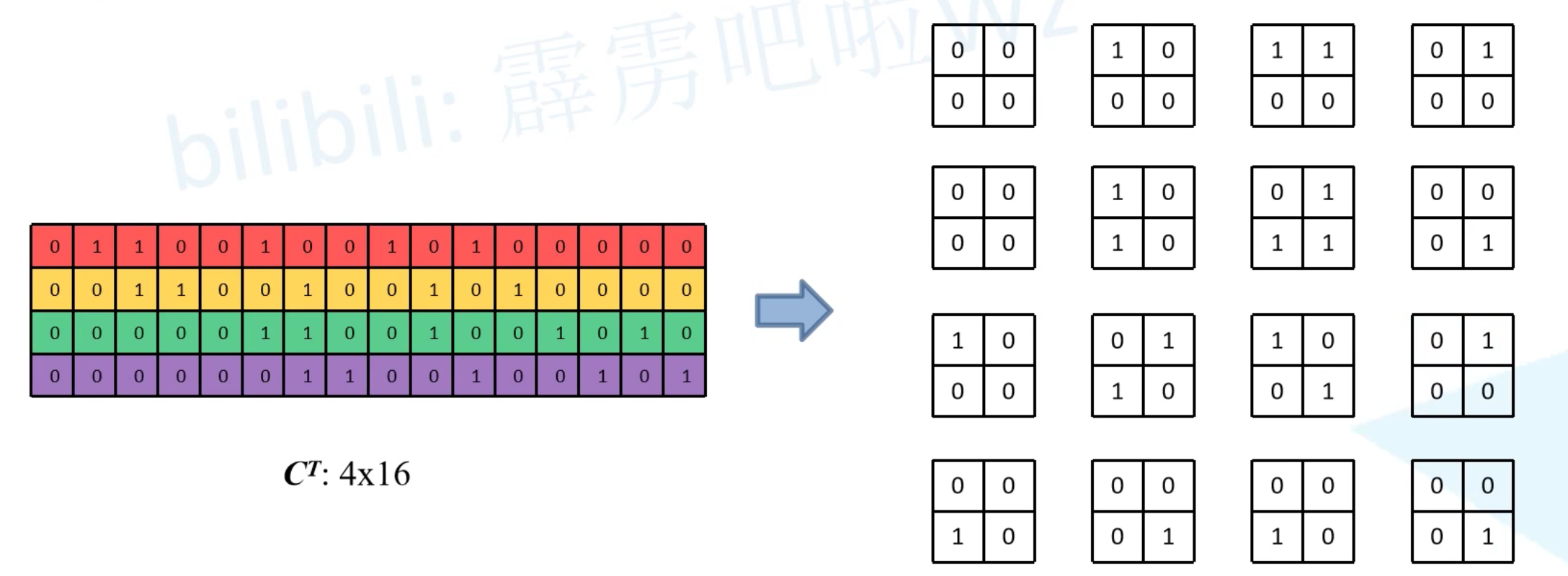
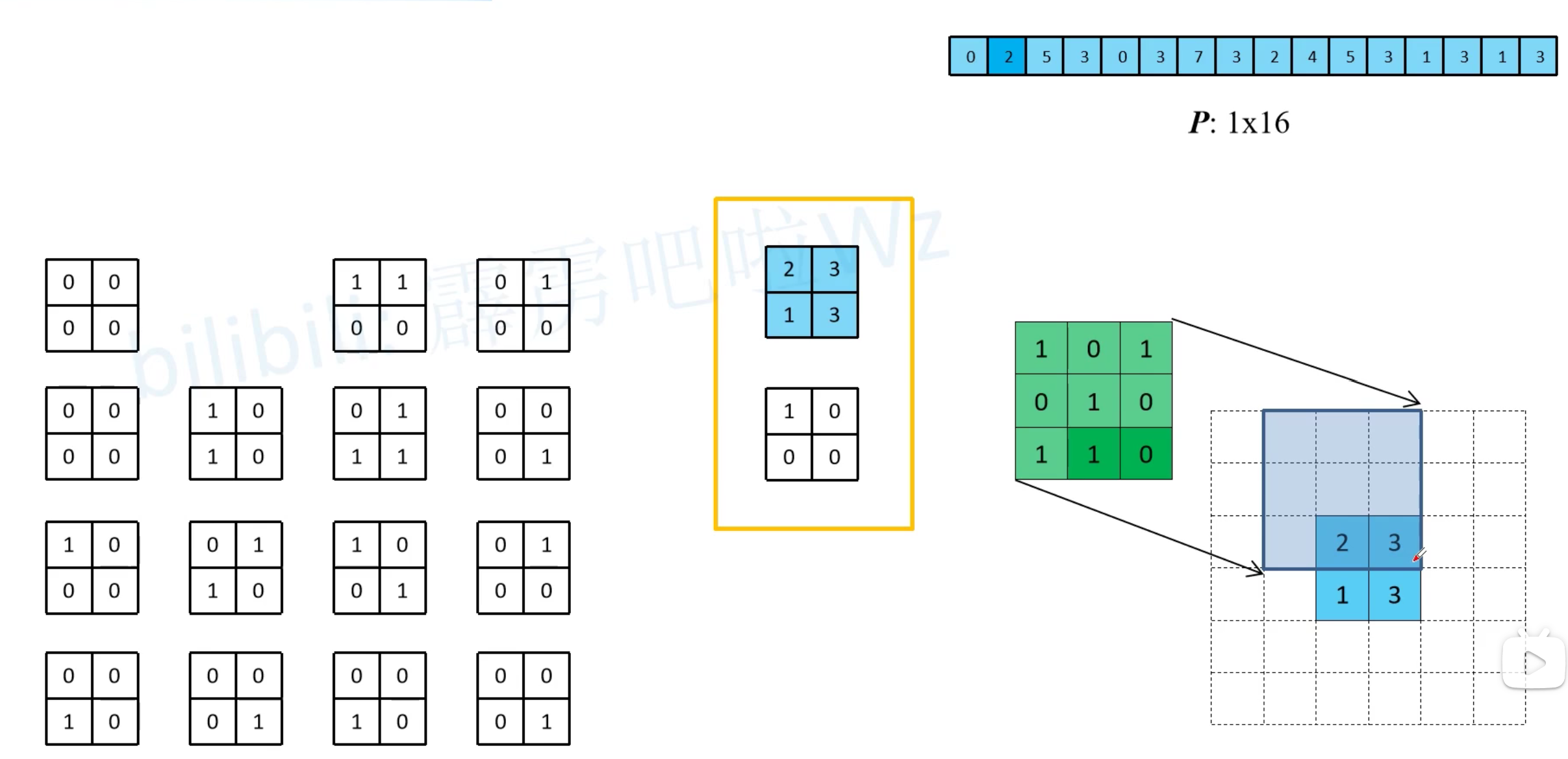
下图清楚的展示了为什么转置卷积的卷积核是原来卷积核上下左右翻转得到的
因为原卷积核与原特征图(4x4)的位置相对于转置卷积核与现特征图(2x2)的位置正好是翻转关系

反卷积和卷积的关系

其实卷积的反向传播过程就是转置卷积的前向传播过程
因为卷积的前向和反向传播分别乘\(C^T\)和\(C^T\)，而转置卷积的前向和反向传播分别乘\(C^T\)和\({(C^T)}^T\)

代码实现

import torch
import torch.nn as nn

def transposed_conv_official():
    feature_map = torch.as_tensor([[1, 0],[2, 1]], dtype=torch.float32).reshape([1, 1, 2, 2])
    print(feature_map)
    trans_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1,
                                    kernel_size=3, stride=1, bias=False)
    trans_conv.load_state_dict({"weight": torch.as_tensor([[1, 0, 1],
                                                           [0, 1, 1],
                                                           [1, 0, 0]], dtype=torch.float32).reshape([1, 1, 3, 3])})
    print(trans_conv.weight)
    output = trans_conv(feature_map)
    print(output)


def transposed_conv_self():
    feature_map = torch.as_tensor([[0, 0, 0, 0, 0, 0],
                                   [0, 0, 0, 0, 0, 0],
                                   [0, 0, 1, 0, 0, 0],
                                   [0, 0, 2, 1, 0, 0],
                                   [0, 0, 0, 0, 0, 0],
                                   [0, 0, 0, 0, 0, 0]], dtype=torch.float32).reshape([1, 1, 6, 6])
    print(feature_map)
    conv = nn.Conv2d(in_channels=1, out_channels=1,
                     kernel_size=3, stride=1, bias=False)
    conv.load_state_dict({"weight": torch.as_tensor([[0, 0, 1],
                                                     [1, 1, 0],
                                                     [1, 0, 1]], dtype=torch.float32).reshape([1, 1, 3, 3])})
    print(conv.weight)
    output = conv(feature_map)
    print(output)


def main():
    transposed_conv_official()
    print("---------------")
    transposed_conv_self()


if __name__ == '__main__':
    main()

参考b站视频