凸优化
凸优化 convex optimization
Convex Optimization – Boyd and Vandenberghe (stanford.edu)
凸优化问题的形式
\[\min f_0(x)\\
\begin{align}
s.t. \ &f_i(x) \le 0 \quad &i=1,2,\cdots,m\\
&h_i(x)=0 \quad &i=1,2,\cdots,p
\end{align}
\]
其中目标函数\(f_0(x)\)和不等式约束\(f_i(x)\)均为凸函数，\(h_i(x)\)为仿射函数
约束条件的小于或等于0就是划分了可行域的范围
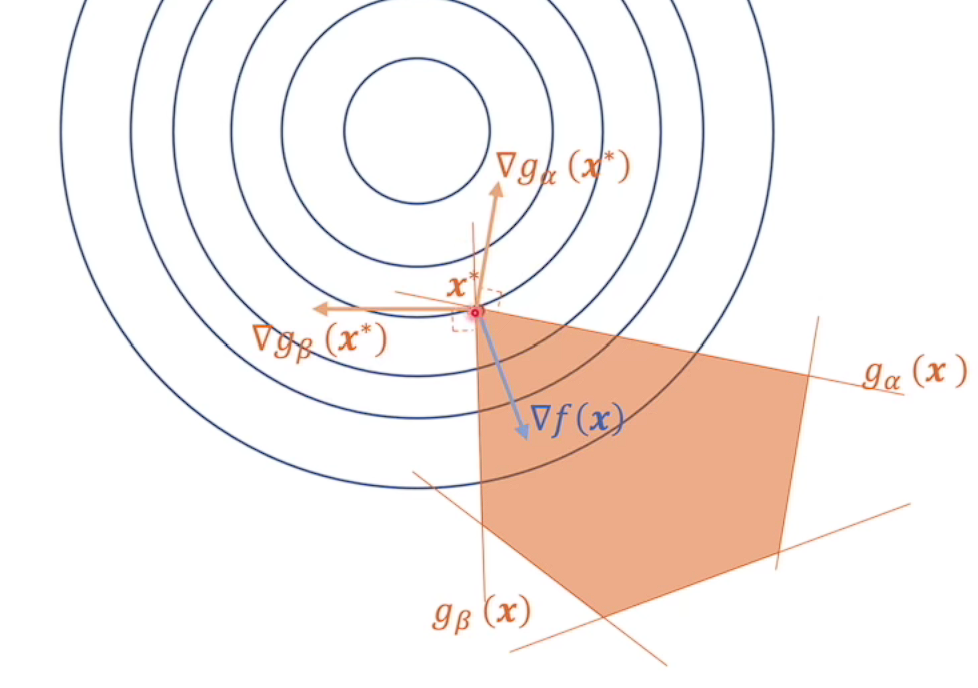
凸优化模型的分类
在处理优化问题时，我们总是尝试将面对的问题模型转化或者松弛成凸优化模型，常见的凸优化模型如下（但不限于）：
线性规划问题
线性规划问题的数理化定义为：
二次优化问题
二次优化问题的数理化定义为：
其中，\(P\)为正定矩阵
二阶锥模型
二阶锥问题的数理化定义为：
