拉格朗日函数 Lagrangian Function
拉格朗日乘数法 Lagrange Multiplier Method
用于求有条件约束时的极值问题,将含有n个变量和k个约束条件的约束优化问题转化为含有n+k给变量的无约束优化问题 更多细节可查看拉格朗日函数
$\lambda$为拉格朗日乘子 $F(x,\lambda)=f(x)+\sum\lambda_i g_i(x_i)$ 如果$f(x)$最小值在所有约束条件的可行域内,则所有约束条件都是松弛的,此时对应的$\lambda_i = 0$约束不等式
为什么拉格朗日函数中的约束不等式对应的拉格朗日乘子$\lambda_i \ge 0$ 这里参考了考虑约束最优化问题(极大化问题可以简单地转换为极小化问题,这里仅讨论极小化问题):
\[\begin{align*}
&\displaystyle\min_{x \in R^n} f(x) \quad\\
s.t. \ &f_i(x) \le 0 &i=0,1,\cdots ,m\\
&h_i(x) = 0 &i=1,2,\cdots,p
\end{align*}
\]
上面的优化问题不一定是凸问题
引入拉格朗日乘子之后得到
\[L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^n \lambda_i f_i(x)+\nu_i h_i(x), \quad, \lambda \ge 0
\]
\(\lambda_i \ge 0\)为了强制要求所有的约束条件必须被满足
当\(x\)违反约束条件时,即不在可行域中时,\(f_i(x)>0\), 调整\(\lambda\)最大化\(L\)的过程使得\(L(x,\lambda)=\infty\),之后的最小化过程即将该值忽略
而当\(x\)满足约束条件时,即在可行域中时,\(f_i(x) \le 0\), 调整\(\lambda\)最大化\(L\)的过程使得\(L(x,\lambda)\)取到最大值0
\[\max_{\lambda \ge 0}L=
\begin{cases}
\infty,& x \notin domL\\
f_0(x),& x \in domL\\
\end{cases}
其中 \quad domL=\mathcal D \times R^m \times R^p
\]
最小化同理,如果不限制\(\lambda \ge 0, \quad \inf L(x,\lambda,\nu)\rightarrow -\infty\)
所以当弄清楚拉格朗日乘子的作用时,就可以理解为什么\(\lambda_i \ge 0\)了,这么设定\(\lambda_i\)就是为了把不满足约束条件(即不在可行域中的\(x\))pass掉
凸优化问题的拉格朗日函数形式
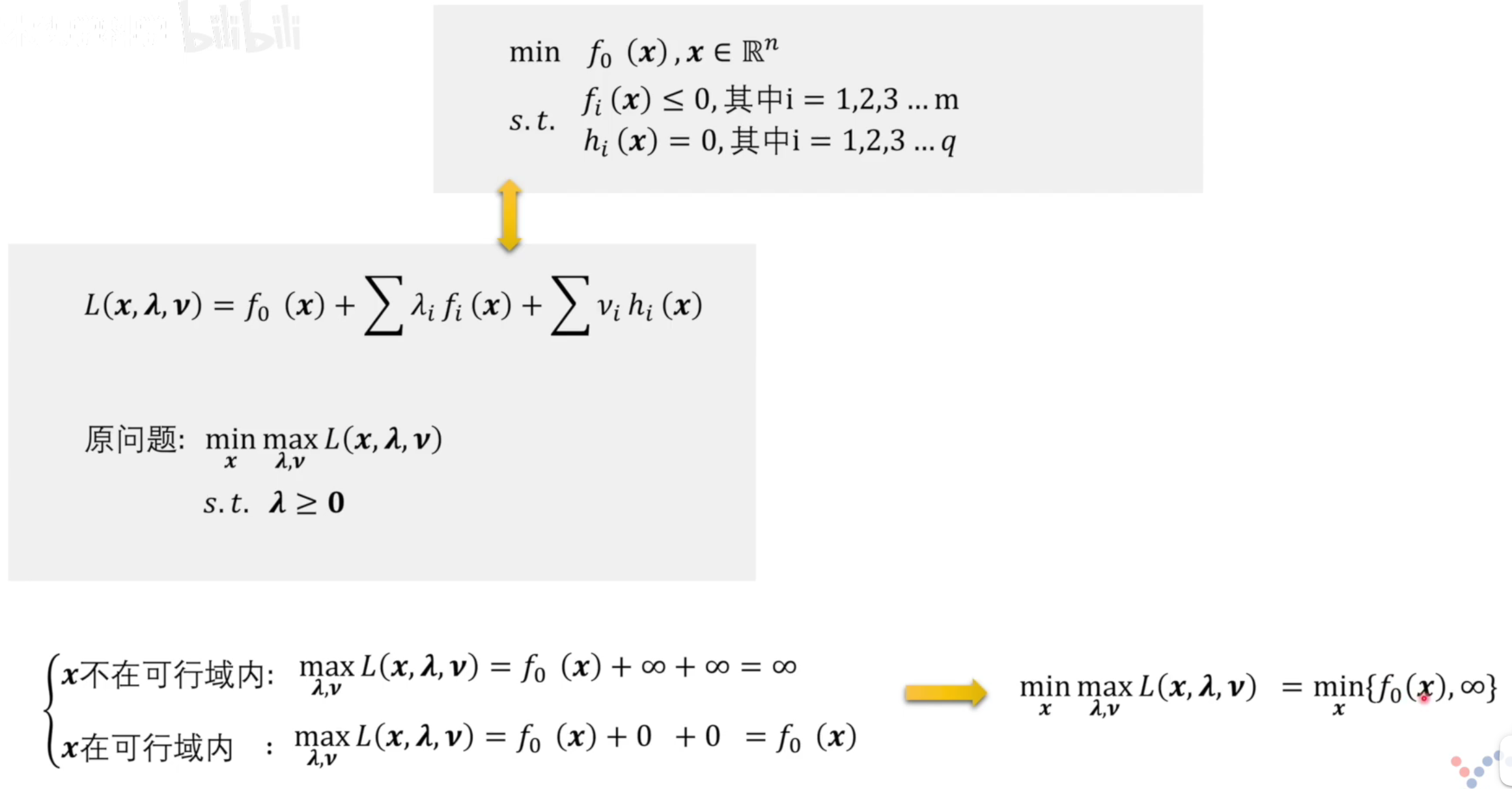
因为对于\(\lambda, \nu\)求最大值都会被最后的对于x求最小值而忽略
所以最后就是求\(f(x_0)\)的最小值和\(g_i(x)=0\)的问题
要注意的一点:虽然最后一项\(\sum \nu_i h_i(x)\)恒等于0,但梯度不一定为0,所以不能省略
下一篇:拉格朗日对偶问题


