凸集 Convex Sets

仿射集 Affine Sets

线和线段

线 line

\[x_1 \ne x_2 \in R^n\\\ y=\theta x_1+(1-\theta) x_2 \]

线段 line segment
上述条件当带有约束条件\(0 \le \theta \le 1\)时,\(y\)是线段

仿射集affine set

\[x_1,x_2 \in C, \theta \in R\\ \theta x_1+(1-\theta)x_2 \in C \]

也就是说,仿射集中任意两点的线性组合仍然属于仿射集,注意必须满足约束条件coefficients sum to one
仿射集一定是凸集

仿射组合affine combination

An affine set contains every affine combination of its points

\[x_1,\cdots,x_k \in C, \theta_1+\cdots,+\theta_k=1\\ \theta_1 x_1+\cdots+\theta_k x_k {\rm is an affine combination} \]

仿射包 affine hull

\({\rm aff} \ C\)是一个仿射包,通俗理解，仿射包就是包含集合\(C\)的最小的仿射集合

\[{\rm aff}C=\{\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n|x_i \in C,\theta_1+\theta_2+\cdots+\theta_n=1\} \]

对任意集合A，增加最少的元素使A变为仿射集B，则仿射集A是B的仿射包，即A是包含B的最小仿射集。
线段的仿射包是包含这条线段的直线，平面多边形（三角形，正方形等）的仿射包是包含此多边形的整个平面，仿射集的仿射包是它自身

仿射集的子空间

上述仿射集成立的条件必须有\(\sum_{i=1}^k \theta_i=1\)的约束
那么什么情况下可以去掉该约束呢
从下图可以看出

• 不过原点的直线(仿射集C)上任取两点,向量\(x_1,x_2\)的和\(x_1+x_2\)(其实是线性组合\(\alpha \cdot x_1+\beta \cdot x_2,\ \alpha=\beta=1\),此时不满足\(\sum_{i=1}^k \theta_i=1\)的约束)并不属于仿射集C
• 但过原点的直线(另一个仿射集)上向量的任意线性组合依然在该仿射集上（因为\(x_1,x_2\)线性相关）

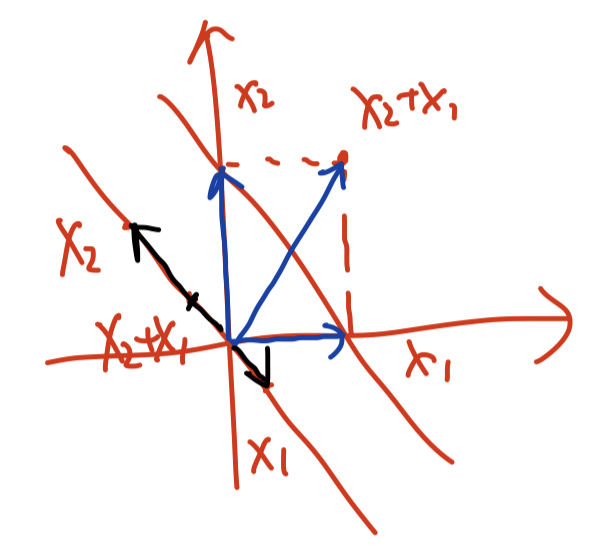
那么貌似有些头绪了，下面定义

\[V=C-x_0=\{x-x_0|x \in C\} \]

V是C的子空间,这个子空间中向量的任意线性组合依然属于子空间

\[v_1,v_2 \in C, \ v_1+x_0 \in C, v_2+x_0 \in C\\ {\rm since} \quad \alpha+\beta+(1-\alpha+\beta)=1\\ \alpha v_1+\beta v_2+x_0=\alpha (v_1+x_0)+\beta (v_2+x_0)+(1-\alpha-\beta)x_0 \in C\\ {\rm then} \quad \alpha (v_1+x_0)+\beta (v_2+x_0) \in V\\ \]

因此仿射集\(C\)可以表示为其子空间\(V\)加上一个偏置

\[C=V+x_0=\{v+x_0|v \in V\} \]

即对仿射集C， 首先选出C中任意一个元素，再用C中所有元素都同时减去这个元素，此时得到一个新的集合，这个集合必有一个0元素，这样得到的新集合就是一个与C相关的子空间。
子空间相当于是基于\(x_0\)做了一个平移，使之必过原点，子空间是仿射集。

相对内部 relative interier

相对内部

\[{\rm relint} \ C={x \in C|B(x,r) \cap \ {\rm aff} C \subseteq C {\rm forsome} r>0} \]

相当于一个不包含边缘的开集

凸集 Convex Sets

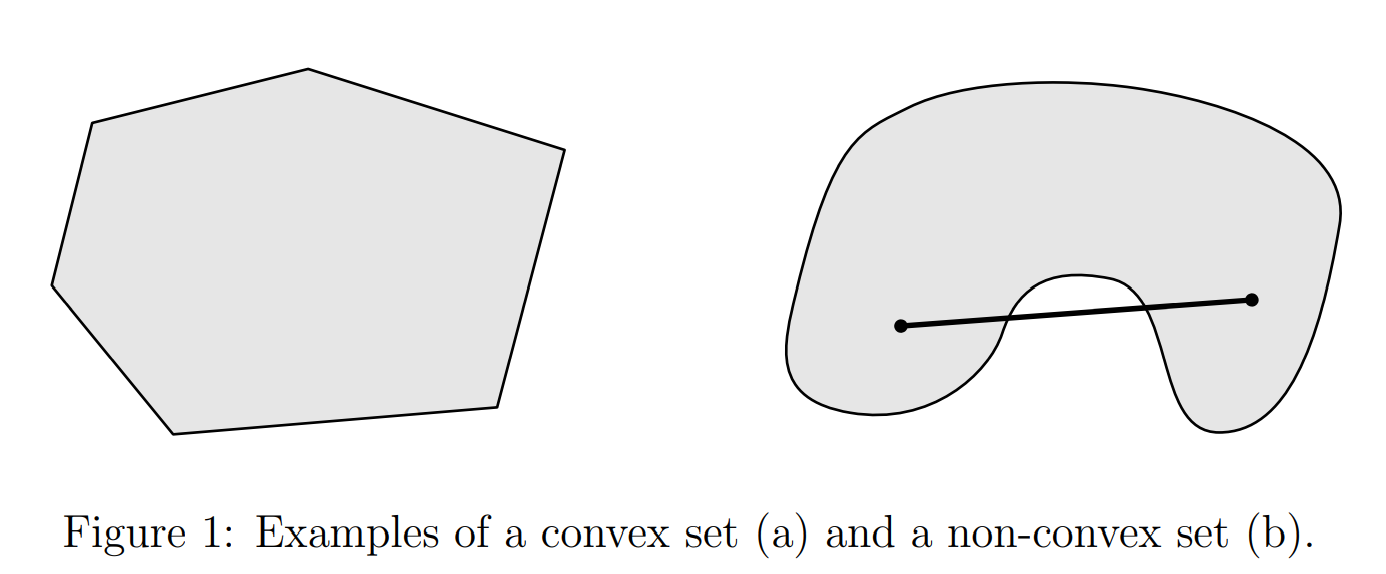
凸集的定义

$$ \forall x_1,x_2 \in C, 0\le\theta\le1\\ \theta\cdot x_1+(1-\theta)\cdot x_2 \in C $$ 也就是说集合中的两点连成的线段也要在集合中,凸集比仿射集多的限制就是$\theta \in [0,1]$

凸组合 convex combination

\[x_1,\cdots,x_k \in C, \theta_1+\cdots,+\theta_k=1, \theta_i \ge 0\\ \theta_1 x_1+\cdots+\theta_k x_k \ is \ an \ convex \ combination \]

凸包 convex hull

\[{\rm conv}C=\{\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n|x_i \in C,\theta_i \ge 0,\theta_1+\theta_2+\cdots+\theta_n=1\} \]

凸包是包含\(C\)(任意集合,不一定是凸集)的最小凸集
所以凸包就是将非凸集合通过凸组合的定义形式形成一个凸集

凸包的例子如下图所示：

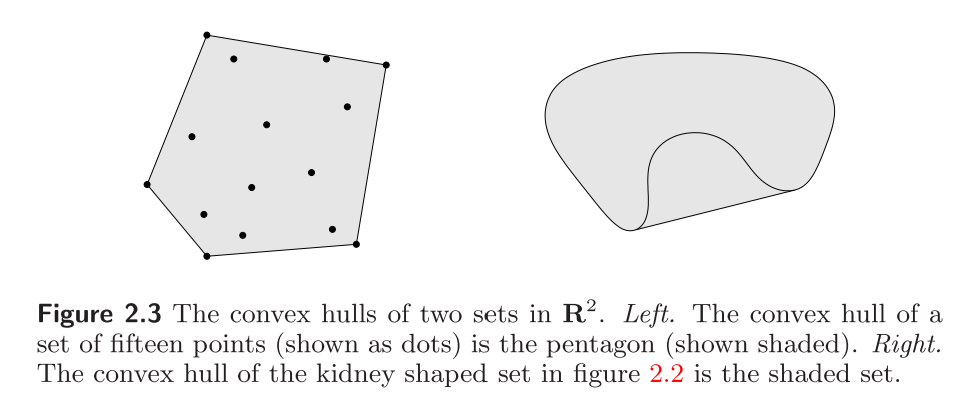
锥 Cones

锥的定义

Cone 又叫 nonnegative homogeneous

\[\forall x \in C, \theta \ge 0\\ \theta x \in C \]

锥必过原点，如在二维平面中一条以原点作为端点的射线是锥，由多条这样的射线构成的集合也是锥。
比如：齐次方程组的解是锥

凸锥 convex cone

A set C is a convex cone if it is convex and a cone.

\[\forall x_1,x_2 \in C, \theta_1,\theta_2 \ge 0\\ \theta_1x_1+\theta_2x_2 \in C \]

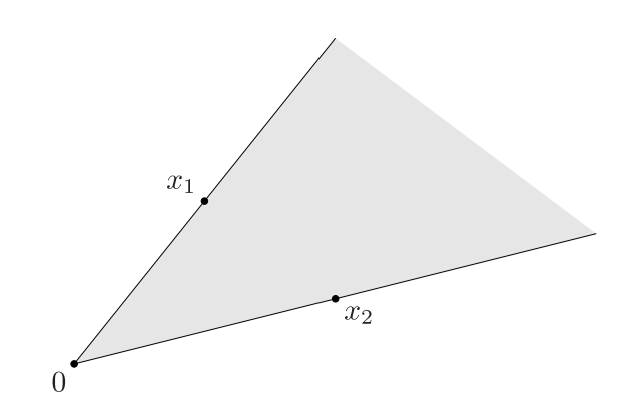
锥组合 conic combination

\[x_i \in C, \theta_i \ge 0\\ \theta_1 x_1+\cdots+\theta_k x_k \ is \ an \ conic \ combination \]

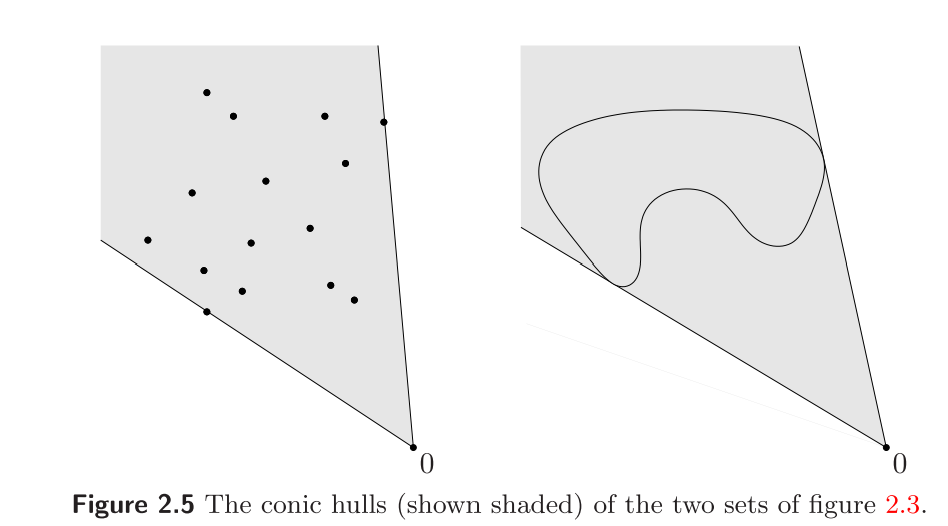
锥包 conic hull

与前面仿射包和凸包的定义类似,锥包就是所有锥组合的集合

\[\{\theta_1x_1+\cdots+\theta_kx_k|x_i \in C, \theta_i \ge 0\} \]

仿射集、凸集、凸锥

仿射集：\(\sum \theta_i=1\)
凸集：\(\sum \theta_i=1,\theta_i \ge 0\)
凸锥：\(\theta_i \ge 0\)

常见的凸集

The empty set; single point; the whole space \(R^n\)

Any line is affine. If it passes through zero, it is a subspace, hence also a convex cone.

A line segment is convex, but not affine (unless it reduces to a point).

A ray, which has the form \(\{x0 + θv | θ ≥ 0\}\), where \(v \ne 0\), is convex, but not affine. It is a convex cone if its base \(x_0\) is 0.

Any subspace is affine, and a convex cone (hence convex).

\(\forall x_1,x_2 \in C, \theta \in \R \Rightarrow \theta\cdot x_1+(1-\theta)\cdot x_2 \in C\)，那么\(C\)是仿射函数，仿射集是凸集，仿射集的交集也为凸集

超平面 Hyperplanes

超平面是仿射集,凸集

\[\{x | a^Tx=b \} \]

半空间 Halfspace

半空间是凸集,但不是仿射集

\[\{x | a^Tx \ge b \} \]