拉格朗日对偶问题 Lagrange Dual Problem

拉格朗日对偶问题

原问题

\[\min f_0(x)\\ \begin{align*} s.t. \ &f_i(x) \le 0 \quad &i=1,2,\cdots,m\\ &h_i(x)=0 \quad &i=1,2,\cdots,p \end{align*} \]

化成拉格朗日函数形式

\[L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^m \lambda_i f_i(x)+\sum_{i=1}^p \nu_i h_i(x) \]

对偶函数

\[g(\lambda,\nu)=\min_x L(x,\lambda,\nu) \]

对偶问题

\[\max_{\lambda,\nu}g(\lambda,\nu)=\max_{\lambda,\nu} \min_x L(x,\lambda,\nu)\\ s.t. \lambda \ge 0\\ \]

对偶问题也可写作有约束条件的形式

再强调一遍,最里层是拉格朗日函数,次外层是对偶函数,把对偶函数(凹函数)最大化就是对偶问题(凸问题),最大值就是上确界

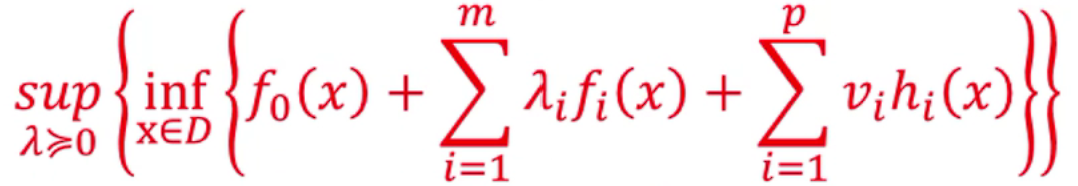
上帝视角再看一遍

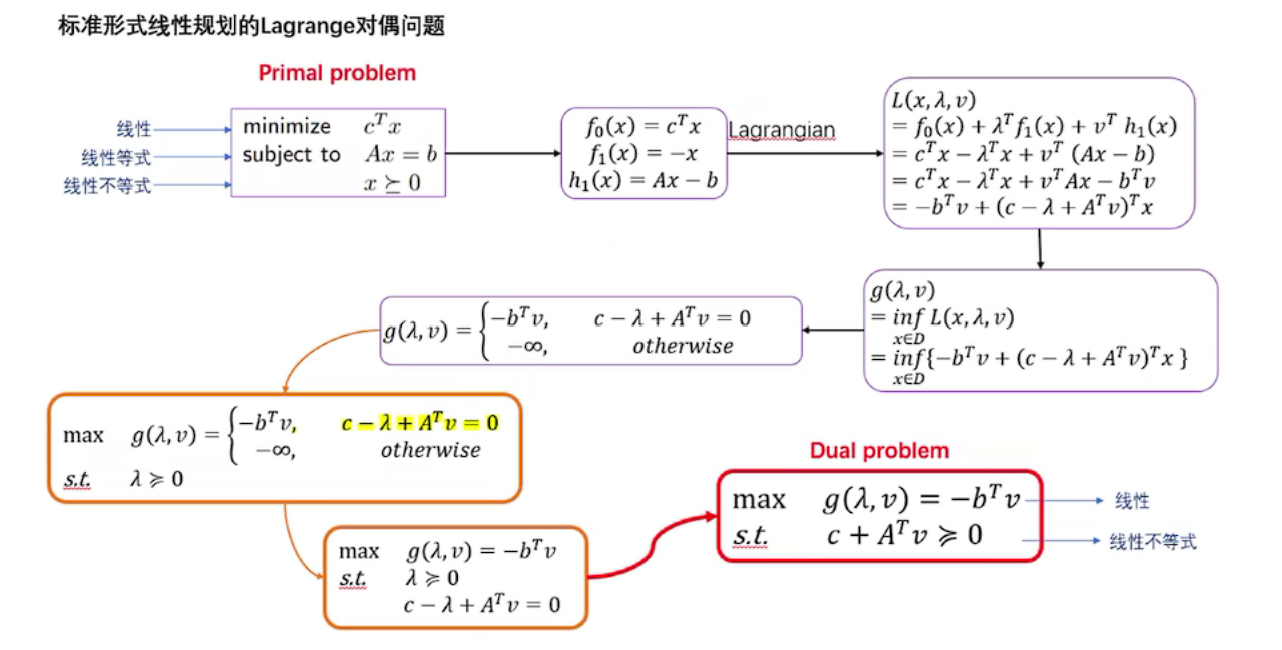
原问题和对偶问题的关系

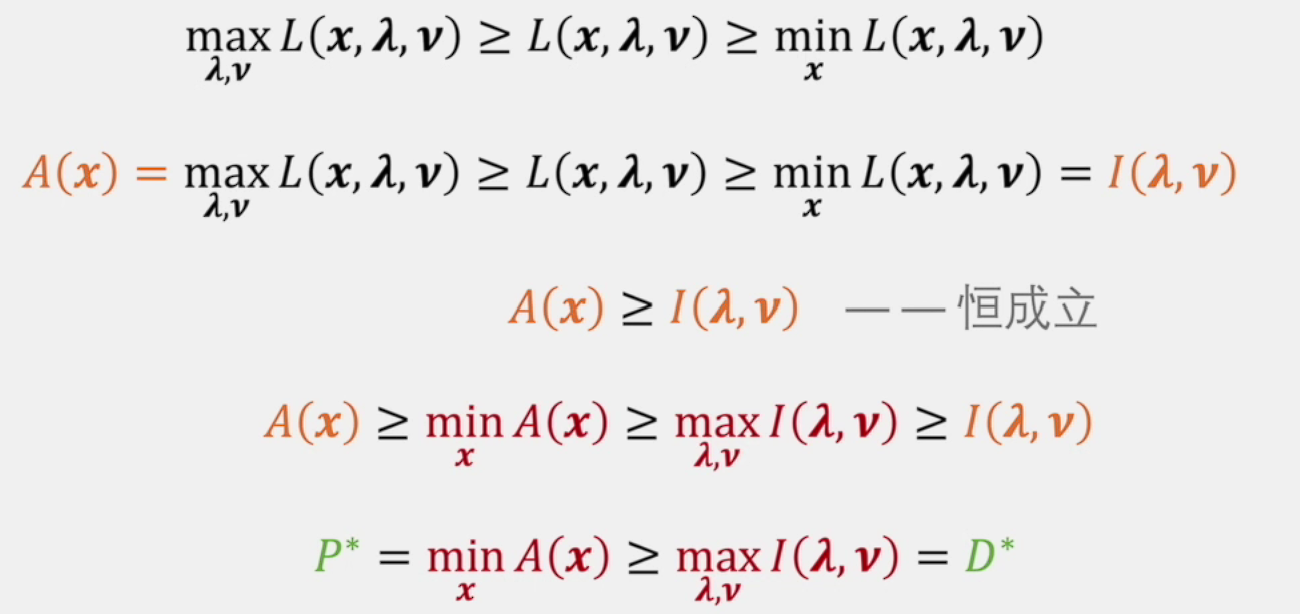
所以原问题的解$\ge$对偶问题的解
那么问题来了，何时原问题才能和对偶问题有相同的解呢？

问题简化

首先，先将问题简化一下

注意，此时原问题中$x$的可行域(feasible region)在约束空间中，而对偶问题中的$x$无约束
所以$G_1 \subseteq G_2$
这样简化之后就可以从图像上直观的表示出来，其中可以把$t$看作$y$，把$u$看作$x$，那么就可以表示成一个线性函数

图像直观理解原问题和对偶问题

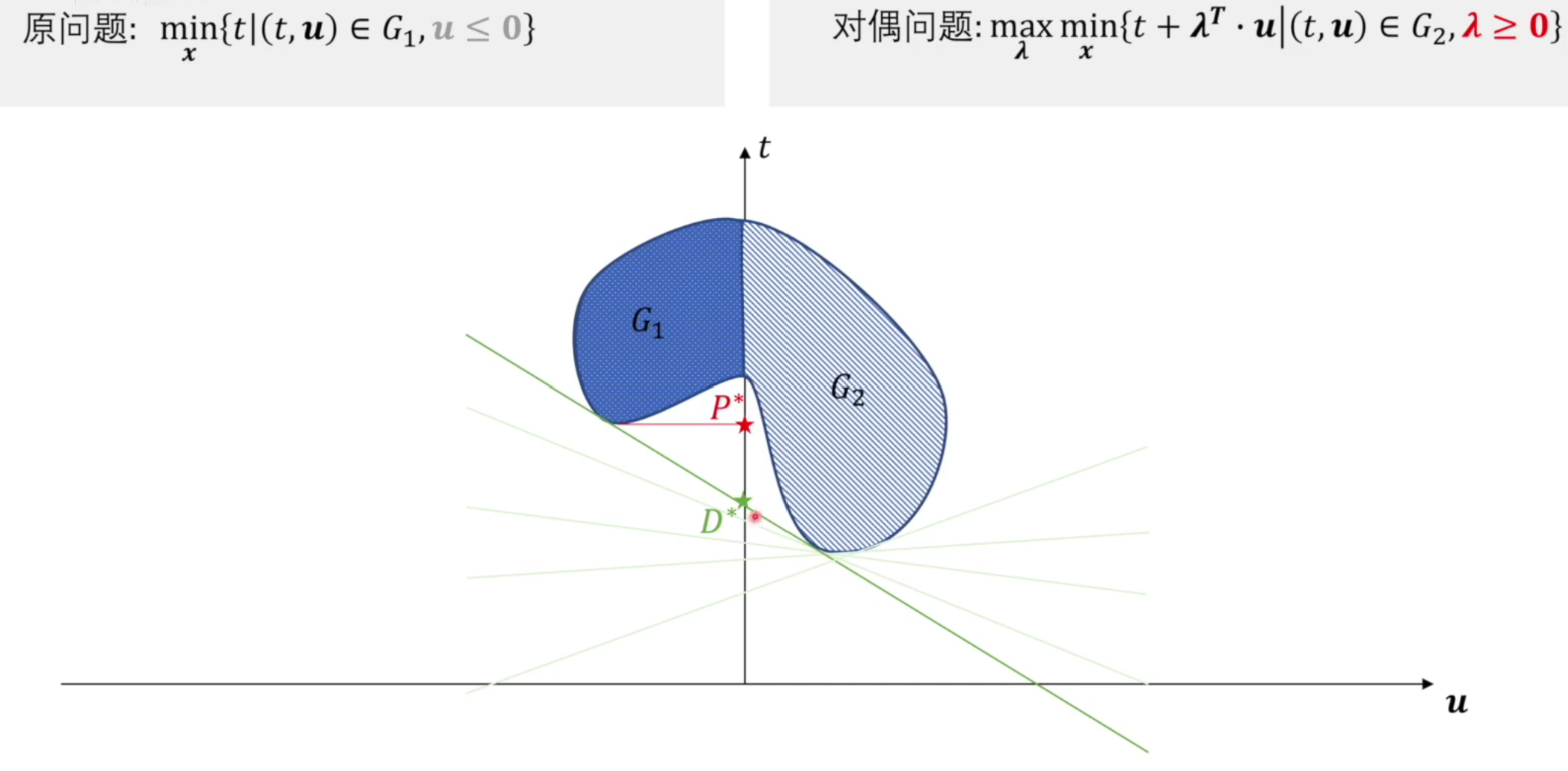
因为$u \le 0$，所以$G_1$在左半部分，而假设$G_2$是整个蓝线围成的域
原问题找到最小值即为$P^*$
对偶问题先对于$x$找函数的最小值，再通过调整斜率，找到对于$\lambda$变量，函数的最大值

有两点需要注意

因为$\lambda \ge 0$，而函数的斜率为$-\lambda^T$，所以斜率必然$\le$0
要与左边相切且与右边相切才能满足最大最小条件

这里不太理解，先调整$x$得到最小值，再调整$\lambda$使函数最大，此时$x$已为定值，调整$\lambda$后还与右边相切吗？

问题解决,再看一遍上面那个总流程图

\[\begin{align*} g(\lambda,\nu)&=\inf_{x \in D} L(x,\lambda,\nu)\\ &=\inf_{x \in D}{-b^T\nu+(A^T\nu-\lambda+c)^Tx}\\ \end{align*} \]

对偶函数中想要最小化的式子是一个仿射函数，可以理解为一条直线，无界
所以只好让斜率=0(说斜率不太准确,高维空间应该是和原函数相切的超平面)，这个斜率取0，后面就调节截距了，所以确定后始终是相切的

「这个过程是在每个固定斜率下求最小截距，然后从在不同斜率下求得的最小截距中找最大的」具体见这篇博客

直线的截距$D^*$即为对偶问题的解
从图像也可看出原问题的解大于等于对偶问题的解，这种关系其实是一种若对偶关系

那么什么条件下原问题和对偶问题是等价的呢？

强对偶关系

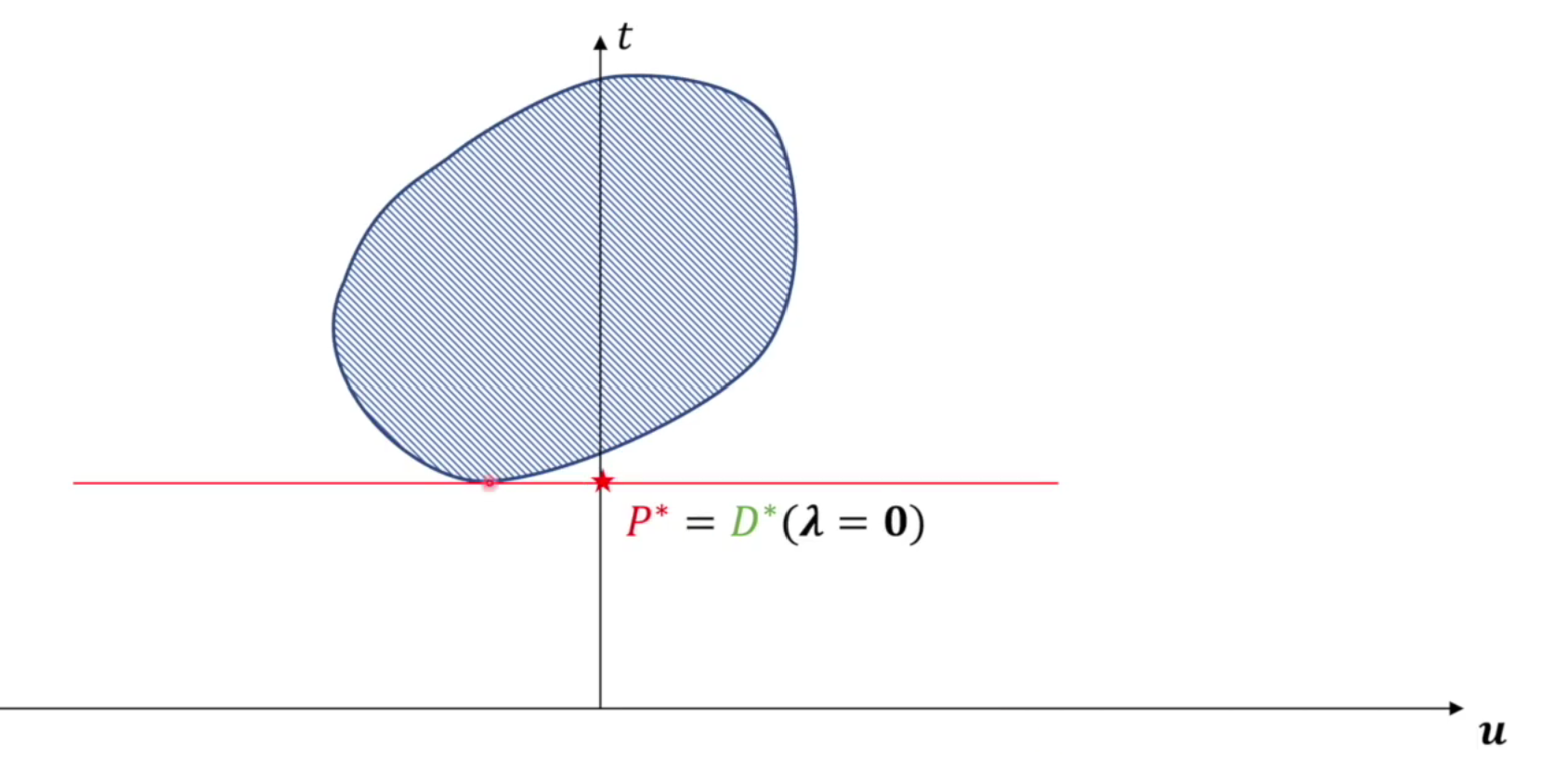
不难想象，可行域的范围是一个凸集时，两值相等（注意：斜率一定$\le 0$）
但是，$G$为凸集只是强对偶的充分非必要条件
比如下图的可行域范围是非凸集，但原问题和对偶问题依然等价

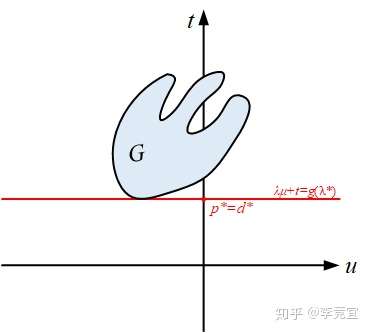
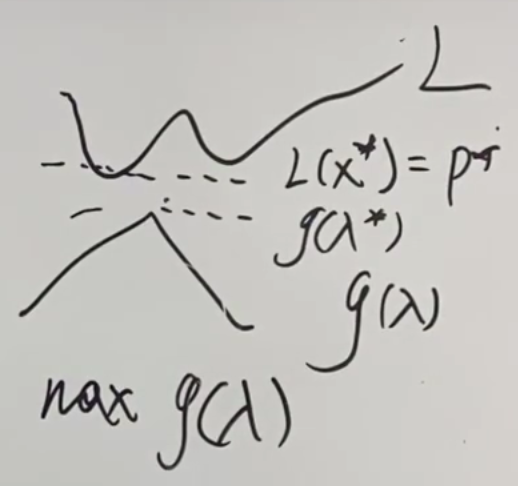
Slater条件

其中$relint \ D$为相对内部

只有满足了Slater条件，凸优化问题才是强对偶问题，是充分条件

KKT条件

KKT条件是强对偶问题的必要条件

如果$x$在可行域内，$g_i(x)$是松弛的，此时的$g_i(x) \le 0$，$\lambda_i=0, \lambda_ig(i)=0$
如果最小值点不在可行域内，那么极值点在边界上，$g_i(x)=0$，$\lambda_ig(i)=0$
上述的紧致和松弛也就对应着前面强对偶关系的两种情况的图像

拉格朗日对偶问题的好处

为什么费尽周折的去转化成对偶问题呢？
因为原问题不一定是凸优化问题
然而转化成的对偶问题一定是凸优化问题(凹函数)

应用

最后再回到机器学习的应用中
在求最大熵的时候，就是将原问题转化为对偶问题处理的

转化成对偶问题，先将P的形式定下来，就是确定了模型，然后再调整$\lambda$，也就是调参的过程
但在神经网络中，由于有隐藏层的存在，调整参数$\lambda$后，$x,y$的值不再是已经确定的了，还要重新计算，所以求最小值的过程其实与最大化相互耦合

所以从整体来看并不是凸优化问题，但通过反向传播，在最后的输出层上形成一个局部的凸优化问题

神经网络相当于一个筛选器，把现实中非凸优化的问题转化成凸优化问题，通过隐藏层只留下凸优化的因素，送到最后的输出层

Reference

https://zhuanlan.zhihu.com/p/103961917

https://www.bilibili.com/video/BV1HP4y1Y79e?from=search&seid=10704814736374919657&spm_id_from=333.337.0.0