条件熵 最大熵 Softmax

条件熵

使\(P(y|x)\)熵最大，怎么求？

\[H^{(A)}=-\sum_{i=1}^nP(y_i^{(1)}|x)\log P(y_i^{(1)}|x)\\ H^{(B)}=-\sum_{i=1}^nP(y_i^{(2)}|x)\log P(y_i^{(2)}|x) \]

条件熵的定义

\[\begin{align*} H(Y|X)&=-\sum_{x,y}P(x)P(y|x)\log P(y|x)\\ &=E(H(Y|X=x^{(k)})) \end{align*} \]

注意，公式中有\(x,y\)两个变量，两层累加

\[H(Y|X)=-\sum_{x,y}P(x)P(y|x)\log P(y|x)\\ H(Y|X)=-\sum_{x,y}\tilde P(x)P(y|x)\log P(y|x)\\ \]

其中\(P(x)\)可以用经验概率\(\tilde P(x)\)来近似代替

\[\max_{x,y}H(Y|X) \]

接着，转换为求最小值

\[\min_{x,y} \sum_{x,y}\tilde P(x)P(y|x)\log P(y|x) \]

最大熵

最大熵问题就是使条件熵\(P(y|x)\)最大
Sigmoid 和 Softmax的本质都是最大熵
上面提到的条件熵，加上两个约束条件，通过拉格朗日乘数法和对偶问题（不展开了，具体可看b站视频，讲的特别好），求出

\[P(y_i|x)=\frac {e^{{\eta}^T} \cdot f(x,y_i)} {\sum_ye^{{\eta}^T} \cdot f(x,y)} \]

这里是不是就十分眼熟了，就是softmax的形式
从这可以看出\(e\)不仅是为了结果大于0这么简单，而是通过求最大熵引入的

Softmax

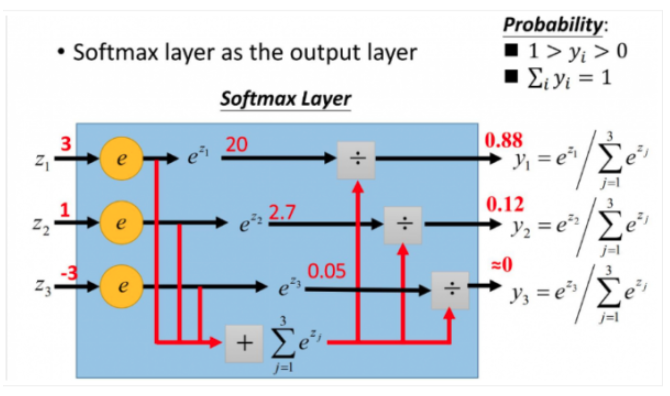
Softmax形式

\[S_i=\frac {e^i} {\sum_{k=1}^n e^k} \]

而sigmoid的形式其实就是softmax的二分类情况
当问题退化成0-1时，因为\(e^0=1\)
softmax就变成了sigmoid的形式

\[Sigmoid=\frac {1} {1+e^{-x}} \]

到了这里，机器学习算法的一半也就完成了，即确定了概率分布的形式

\[\max_{\lambda} \min_{P}L(P,\lambda) \]

应用

最后再宏观的来看一下机器学习的目的，已知一定的样本（数据集），我们希望能够在已有的数据集上扩大适用范围，而扩大后的结果需要与已有的样本特征保持一致
即当\(x\wedge y\in\)训练集时，\(P(y|x)=\tilde P(y|x)\)
而当\(x\vee y \notin\)训练集时，\(P(y|x)\)等于什么呢
在前提\(P(x,y)=\tilde P(x,y)\)和\(P(y|x)\)熵最大下,我们确定了模型的形式
而参数\(\lambda\)该怎么确定呢？
就是构造损失函数，由梯度下降法得到