Eigen库
前言
最近在学习计算机图形学的一些知识,里面要大量运用像矩阵运算这样的线性代数知识,而Eigen库就是一个支持我们用c++语言进行线性代数、矩阵和矢量运算的第三方库。想着后续真正开始写代码后这个库用的应该挺多的,于是就先来简单学习一下这个库。另外学习这个之前最好还是先了解一点线性代数相关的知识,不然一些核心概念也是不好理解的,大概知道什么是矩阵、什么是向量、以及矩阵运算的一些知识和性质就差不多了。
开始
首先我们需要去官网下载这个第三方库,下载完成后解压会得到完整的目录,就比我我放在了E盘下的c++ku目录,现在我们记下这个目录地址E:\c++ku\eigen-3.4.0,这里我都IDE使用的是Visusl Studio2019,我们新建一个项目,右键项目根目录选择属性选项。
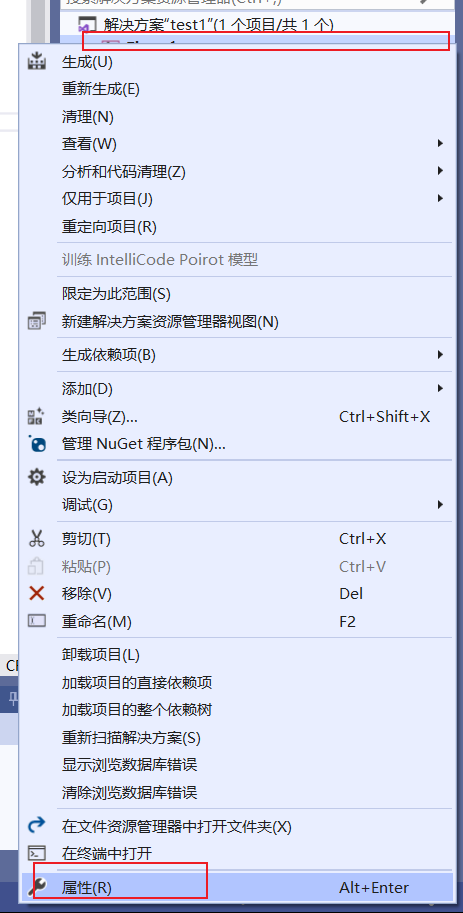
然后把配置和平台选项都改为所有配置和所有平台。最后配置属性一栏选择VC++目录,右侧找到包括目录选项,在里面新增我们刚才的Eigen库的目录即可。

然后我们就可以正常在这个项目中引入使用了。
进入目录我们会发现这个库中有许多模块,如下图所示。
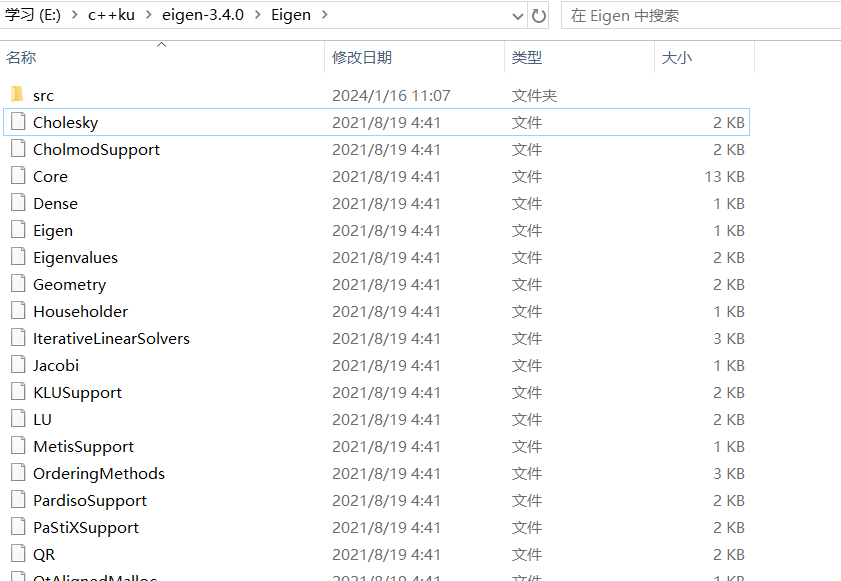
这是一些主要模块的内容和作用,因为我们这里只是简单学习一下这个库的基本使用,不会深入讲解,所以只涉及到Core模块,讲解一下里面的矩阵运算。

Matrix类
矩阵创建
这个类里面主要包含了Matrix(矩阵)和Vector(向量),其实向量也可以看做特殊的矩阵,看作是只有一行或者一列的矩阵。我们首先来看看Matrix模板类,我们创建过程中需要指定一些参数:
1.第一个参数是指明数据类型,和数组道理一样,我们要说明矩阵里存放的什么类型的数据(比如int,float,double等)
2.第二个参数是指明行数,可以写一个整数表示具体行数,也可以写Dynamic,表示不确定大小动态创建。
3.第三个参数是指明列数,和行数一样,可以指明列数也可以动态创建。
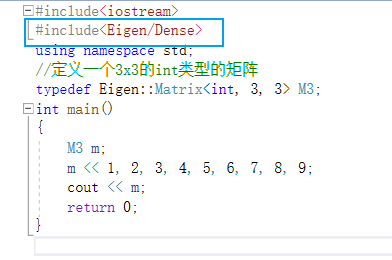
Matrix<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>下面就看一段示例代码。
#include<iostream>
#include<Eigen/Core>
using namespace std;
//定义一个3x3的int类型的矩阵
typedef Eigen::Matrix<int, 3, 3> M33;
//定义一个不确定行和列的int类型的矩阵
typedef Eigen::Matrix<int, Eigen::Dynamic, Eigen::Dynamic> MDD;
int main()
{
//可以像数组那样用大括号赋值
M33 m1{
{1,2,3},
{4,5,6},
{7,8,9}
};
cout<<"m1:3x3"<<endl << m1 << endl;
//可以用重载后的 << 符号复制
M33 m2;
m2 << 1, 2, 3, 4, 5, 6, 7, 8, 9;
cout << "m2:3x3" << endl << m2 << endl;
MDD m3{
{1,2,3,4},
{2,3,4,5},
{3,4,5,6},
};
cout << "m3:3x4" << endl << m3 << endl;
//如果是动态创建的,用这种写法创建一个矩阵时必须指定大小,不然无法创建这个矩阵
MDD m4(3, 4);
m4 << 1, 2, 3, 4, 2, 3, 4, 5, 3, 4, 5, 6;
cout << "m4:3x4" << endl << m4 << endl;
return 0;
}
运行结果如上图所示,可以看到我们成功的创建了矩阵并且输出出来,Eigen库对<<和>>符号进行了重载,所以我们可以直接用来对矩阵输入输出操作。
上面的代码展示了两种比较常用的赋值方法,另外要强调的是,一个矩阵声明之后是没有初始化的,所以矩阵声明之后必须初始化后才能使用。
另外我们还可以对矩阵的元素进行读取和修改。
#include<iostream>
#include<Eigen/Core>
using namespace std;
//定义一个3x3的int类型的矩阵
typedef Eigen::Matrix<int, 3, 3> M33;
//定义一个不确定行和列的int类型的矩阵
typedef Eigen::Matrix<int, Eigen::Dynamic, Eigen::Dynamic> MDD;
int main()
{
//如果是动态创建的,用这种写法创建一个矩阵时必须指定大小,不然无法创建这个矩阵
MDD m4(3, 4);
m4 << 1, 2, 3, 4, 2, 3, 4, 5, 3, 4, 5, 6;
cout << "m4:3x4" << endl << m4 << endl;
cout << "m4(0,0)=" << m4(0, 0) << endl;//获取矩阵元素
m4(0, 0) = 0;//修改矩阵元素
cout << "m4:3x4" << endl << m4 << endl;
cout << "m4(0,0)=" << m4(0, 0) << endl;
return 0;
}我们可以通过m(r,c)的形式获取到矩阵中的任意元素,并进行修改。下图中可以看到我们以及成功的修改了矩阵中的元素的值。

矩阵运算
库中重载了 +、-、*、/等基本的四则运算,可以支持矩阵之间运算和矩阵与数字运算,但是不能直接将两个矩阵相除,矩阵可以除以一个常数。
#include<iostream>
#include<Eigen/Core>
using namespace std;
//定义一个3x3的int类型的矩阵
typedef Eigen::Matrix<int, 3, 3> M33;
//定义一个不确定行和列的int类型的矩阵
typedef Eigen::Matrix<int, Eigen::Dynamic, Eigen::Dynamic> MDD;
int main()
{
//可以像数组那样用大括号赋值
M33 m1{
{1,2,3},
{4,5,6},
{7,8,9}
};
M33 m2{
{2,2,2},
{2,2,2},
{2,2,2}
};
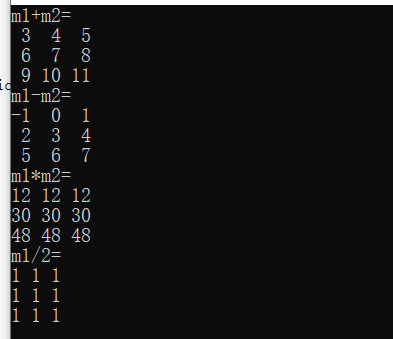
cout << "m1+m2=" << endl << m1 + m2 << endl;
cout << "m1-m2=" << endl << m1 - m2 << endl;
cout << "m1*m2=" << endl << m1 * m2 << endl;
cout << "m1/m2=" << endl << m2/ 2 << endl;
return 0;
}
Vector类
我们可以把向量看做特殊的矩阵,这个矩阵只有一行或者一列。所以我们既可以用上面的Matrix模板类创建向量,只需要设置行或者列为1即可,也可以用Vector模板类创建向量。
#include<iostream>
#include<Eigen/Core>
using namespace std;
//通过Vecort模板类创建
typedef Eigen::Vector<int, 3> V3;
//通过Matrix模板创建
typedef Eigen::Matrix<int, 1, 3> MV3;
int main()
{
V3 v1;
v1 << 1, 2, 3;
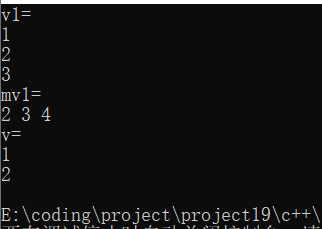
cout << "v1=" << endl << v1 << endl;
MV3 mv1;
mv1 << 2, 3, 4;
cout << "mv1=" << endl << mv1 << endl;
//用封装好的创建
Eigen::Vector2i v;
v << 1, 2;
cout << "v=" << endl << v << endl;
return 0;
}
另外库里面也有已经封装好的一些类型,就比如代码中用到的Vector2i,就表示int类型的2维向量。类似的封装还有很多,矩阵中也有封装好的类型,大家可以自行查看,这里不再过多叙述。
Array类
Eigen库还为我们提供了Array模板类,在矩阵运算中加减操作只能是矩阵之间的运算,一个矩阵不能加或者减一个数字,这可能会导致矩阵运算不能完全满足我们的需求,因此有了这么一个类。他的加减乘除运算只是数字意义上的运算,并不是前面的线性运算,比如两个矩阵相乘的结果是两个矩阵相同位置的元素相乘,和矩阵相乘结果并不相同,而且还可以直接对数字进行加减运算,比如Array加上2,结果就是里面所有元素都加2。
其创建方式和矩阵一样,同样需要指定数据类型,行数和列数。
Array<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>#include<iostream>
#include<Eigen/Core>
using namespace std;
typedef Eigen::Array<int, 3, 3> Ai3;
int main()
{
Ai3 a1{
{1,2,3},
{2,3,4},
{3,4,5}
};
Ai3 a2{
{2,2,2},
{2,2,2},
{2,2,2}
};
cout << "a1+a2=" << endl << a1 + a2 << endl;
cout << "a1+2=" << endl << a1 + 2 << endl;
cout << "a1*a2=" << endl << a1 * a2 << endl;
cout << "a1/a2=" << endl << a1 / a2 << endl;
return 0;
}
同样里面也有封装好的供我们直接使用的类型,这里不再过多叙述。


