【BUAA_2020_软工】个人作业
个人项目作业博客
1. 在文章开头给出教学班级和可克隆的 Github 项目地址(例子如下)。(1')
| 项目 | 内容 |
|---|---|
| 北航2020软工 | 班级博客 |
| 作业要求 | 具体要求 |
| 项目GitHub地址 | 个人项目 |
| 教学班级 | 005(周三上午三四节) |
2. 在开始实现程序之前,在下述 PSP 表格记录下你估计将在程序的各个模块的开发上耗费的时间。(0.5')
见Part 7.
3. 解题思路描述。即刚开始拿到题目后,如何思考,如何找资料的过程。(3')
-
首先读题后,发现:这个问题,一定程度上是一个数学问题,所以思路是按照数学来解题。
-
先不考虑附加题:
-
因为有重合点的情况,一组直线的所有交点,如果不计算并且存下来进行对比,最终的结果是无法保证的,所以先考虑两条直线的交点计算,再考虑存储结构。
-
直线与直线的交点求法有多种,方便电脑计算的有哪些? ------> 调研
-
方法一:
通过点\((x_1, y_1),\;\;(x_2, y_2)\)求得直线\(l1\)的斜率和截距\(k_1, \;b_1\),另一条直线同理
\[\left\{ \begin{array}{rcl} l_1 : y = k_1*x + b_1\\ l_2 : y = k_2*x + b_2 \end{array}\right. \] 联立求解得
\[\left\{ \begin{array}{rcl} &x_0 = \frac{b_2-b_1}{k_1-k_2}&\\ &y_0 = k_1*x_0+b_1& \;\;(or\;y_0 =k_2*x_0+b_2) \end{array}\right. \]
-
方法二:选择√
两条直线:
\[\left\{ \begin{array}{rcl} l_1 : a_1x+b_1y+c_1=0\\ l_2 : a_2x+b_2y+c_2=0 \end{array}\right. \;\;\;\;\;\;\;\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1) \] 把每条直线的两个点带入解析中得:
\[\left\{ \begin{array} \\ a_1 = y_2 - y_1\\ b_1 = x_1 - x_2\\ c_1 = x_2y_1-x_1y_2 \end{array}\right. \] 直线\(l_2\)类似,可以求得未知数\(a_2,b_2,c_2\);之后由(1)得:
\[D = \left|\begin{array}{ccc} a_1 & b_1\\ a_2 & b_2 \end{array}\right| =a_1b_2-a_2b_1\quad\quad(D == 0 则平行否则有交点)\\ x_0 = (b_1c_2-b_2c_1)/D\\ y_0 = (a_2c_1-a_1c_2)/D \] 这种方法的好处在于不用特判斜率不存在的情况,只需要根据D判断是否有交点进行计算即可。
-
-
这时考虑交点的存储结构(使用c++),每当算出一个新的交点时,都需要判断是否已经有这个点,选择三种存储结构
- set:不重复的元素集合,但是在insert的时候有大量的排序操作
- hashMap:通过hash值来存储,每次计算hash值来确定是否已经存在
- vector:无脑push_back,最后扫描去重
经过实测,最终的效果显示,第三种方式的效果更好,set和hashMap因为比较次数太频繁和计算hash值太频繁导致时间消耗很大,难以完成任务。(仅代表个人程序结果,不排除其他因素影响)
-
-
附加题的思路基于上述,考虑直线和圆,圆和圆的交点计算:
-
直线和圆:
-
首先判断直线和圆是否相交,通过计算圆心到直线的距离与半径比较
向量\(\overrightarrow{AB}\)与向量 \(\overrightarrow{AC}\) 的外积的模长代表以AB、AC为边的平行四边形的面积S,利用面积公式 \(S=|\overrightarrow{AB}|*d\),可以得到 \(d = S / |\overrightarrow{AB}|\);
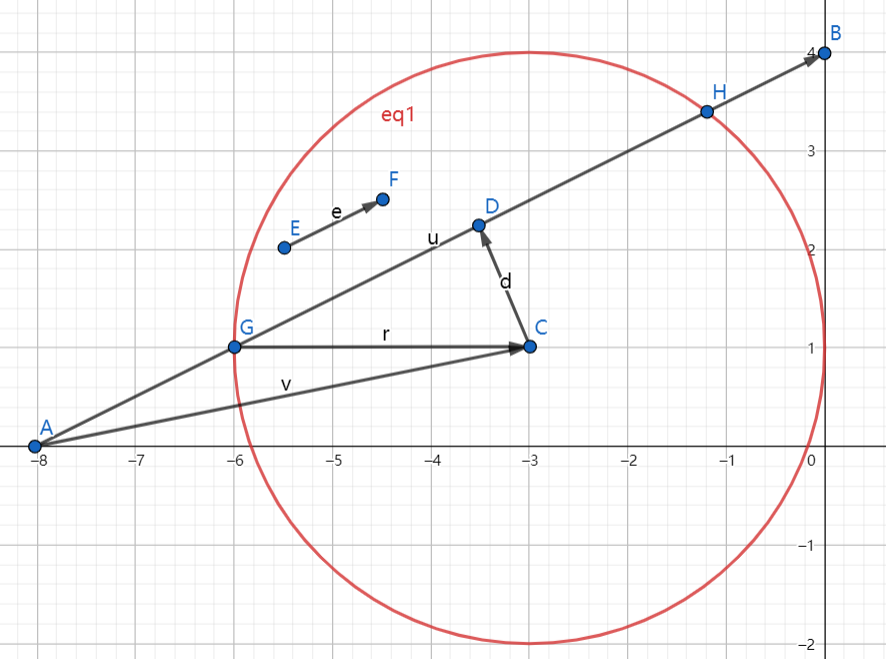
-
若相交则计算交点坐标:
- 求垂足D的坐标:见上图,利用内积公式\(\overrightarrow{AB}·\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cos\theta=|\overrightarrow{AB}|· AD\),所以可以得到AD的长度,则向量\(\overrightarrow{AD}=\frac{AD}{|\overrightarrow{AB}|}·\overrightarrow{AB}\),又因为知道了A点坐标,所以D点坐标就可以得到
- 根据向量\(\overrightarrow{AB}\)求得AB方向的单位向量\(\overrightarrow{e}\),然后,利用直角三角形算出GD的长度为base;
- 此时有了D点坐标,GD长度,和直线AB上的单位向量,可以得到G和H点的坐标:
- \(G = D - \overrightarrow{e} * base\)
- \(H = D + \overrightarrow{e} * base\)
-
-
圆和圆的交点求法有公式法,但是从一篇博客中找到了更好的解法,就是仿照上面按照公式计算,在此不赘述。博客地址
-
4. 设计实现过程。设计包括代码如何组织,比如会有几个类,几个函数,他们之间关系如何,关键函数是否需要画出流程图?单元测试是怎么设计的?(4')
基本要求:
- 类:
- Point:点,因为要判断是否是同一个点,需要实现判断函数
- Line:数据实体,保存输入文件中的信息,并且用于计算
- Circle:类似于Line(附加题需求)
- 函数:
- getCross():计算两条直线的交点,将结果直接保存在全局变量Result中,具体过程为第三部分的方法二
- getAllIntersec():把输入文件读取的Lines信息传入,计算所有的交点,简单的循环计算。
整体逻辑如下图:
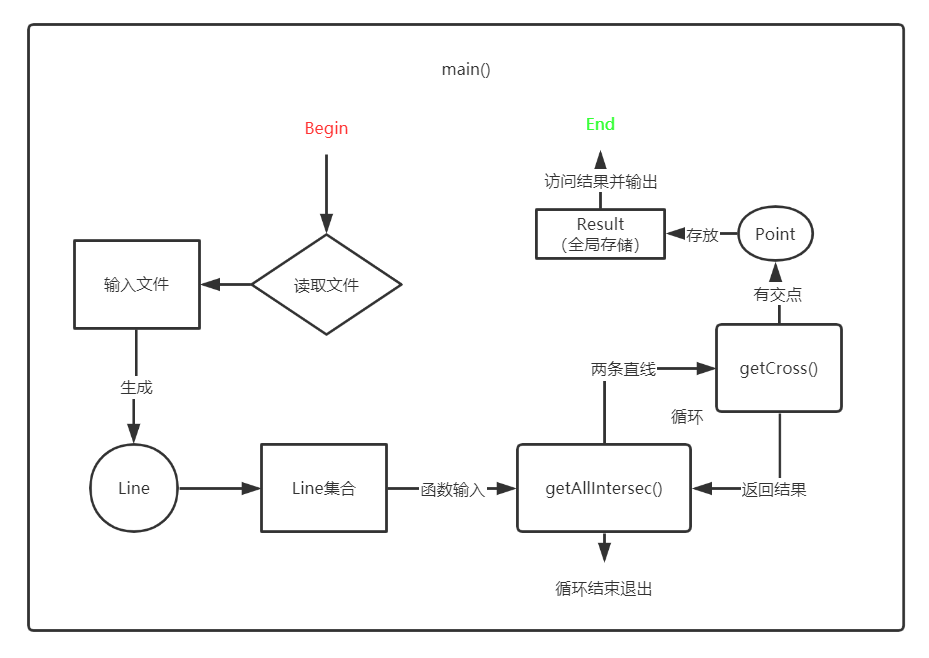
可以看到,Line和Point其实并没有交集,所以这里的Line本质上可以直接删除,只需要记录对应的数据传入getAllIntersec函数即可,不过为了方便附加题的实现,这里没有那么做。
附加题:
- 计算交点分为三种情况:
- 直线与直线:见上图
- 直线与圆:循环遍历直线和每一个圆,调用函数求交点;
- 圆与圆:循环遍历圆和圆,调用函数求交点;
- 读取数据后,把直线存在lines中,圆存放在circles中,然后执行上面的三种计算,交点全部存放在全局结果Result中,最后读取Result的大小即为结果。
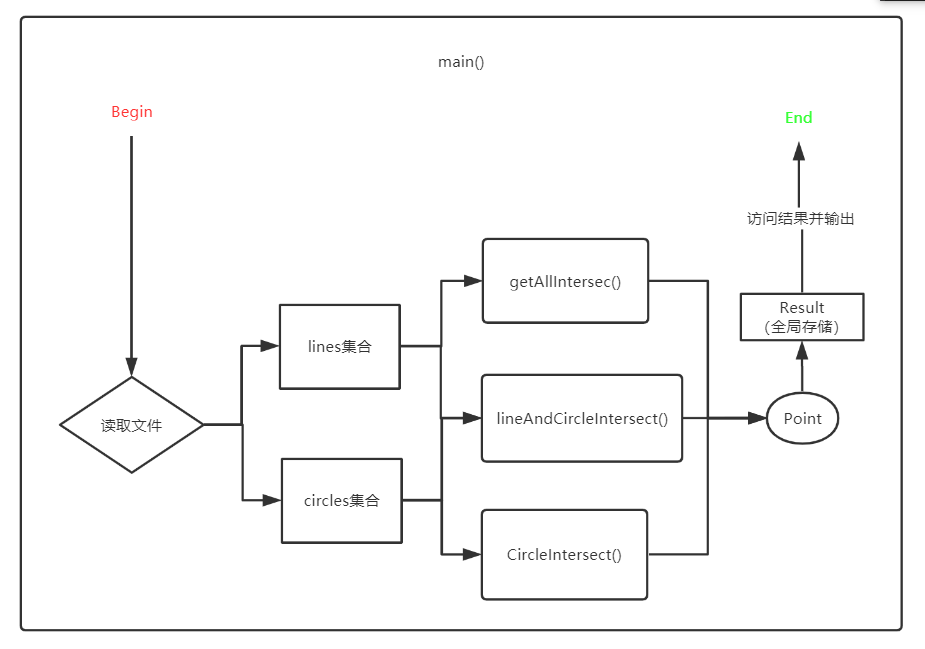
其中直线和圆求交点的代码按照Part 3的附加题思路,具体代码见Part 6.
圆和圆求交点的代码按照博客方法计算,具体思路见Part 6.
(注:因为是按照公式来计算,所以再次不进行详细的赘述,放到Part6)
单元测试:
主要对三个子函数进行测试:
- 直线和支线求交点
- 一条直线无斜率,一条有
- 一条直线平行于x轴,一条正常
- 一条直线无斜率,一条平行于x轴
- 两条直线都有斜率(包含了2,3)
- 直线和圆
- 相交(过圆心与不过圆心两种)
- 相切,一个交点
- 不相交
- 圆和圆
- 相交,外交;
- 相交,内交
- 相切,外切
- 相切,内切(内切又分为两种,c1内切c2,c2内切c1)
- 分离,外离
- 分离,内离
- 以及测试了一些小函数的功能,求外积和内积
最终的测试结果如下:
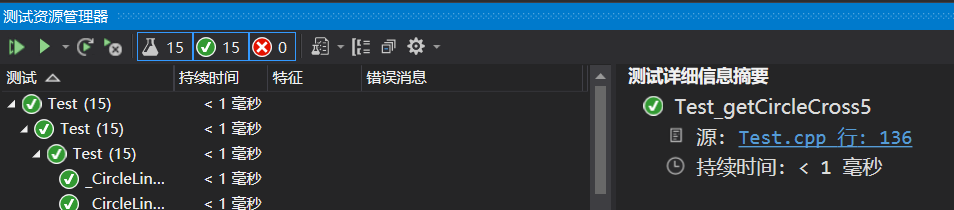
上面的测试时基本的功能测试,为了进一步测试,通过python生成随机数据来进行验证,和同学对拍来验证结果。
通过对拍,找出以下bug:
- 直线与圆相切计算,需要控制精度,否则会因为计算产生的误差导致判断失误
- 圆和圆的内切需要分两种情况
- 以及不同的精度控制范围导致结果的不同,最后测试出自己程序的稳定范围在\(1^{-11} \thicksim 1^{-10}\),这个精度对于直线和直线的计算,已经足够,因为数据范围位\((-100000, 100000)\),最多出现二次项,也就是\(1^{10}\)的级别,对应于精度\(1^{-10}\),而直线和圆,圆和圆的计算,引入的计算误差使得精度到了\(1^{-12}\)时程序结果就不稳定了。
代码分支覆盖率如下图:
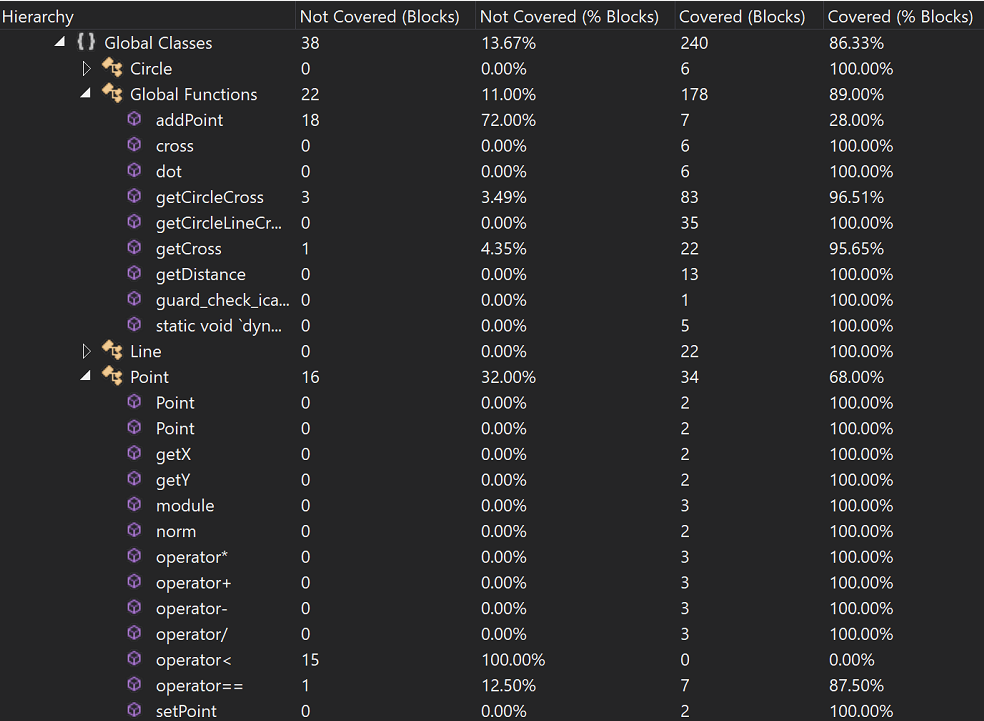
5. 记录在改进程序性能上所花费的时间,描述你改进的思路,并展示一张性能分析图(由 VS 2019 的性能分析工具自动生成),并展示你程序中消耗最大的函数。(3')
从写完最初的版本到现在几乎一直处于改进状态,大概是10个小时吧,期间找了很多资料,也和同学谈论了很多。
-
思考能否不计算出交点坐标就能到最后的结果,目前找不到相关说明,自己也没有头绪;
-
改善固有程序:
- 一开始使用set来存计算出来的Point,这样好处是可以自动去重,问题是数据变大后set.insert()是一个占据很大热点的函数,耗时太多,超时;
- 考虑hashmap,但是一个同学使用的hashmap,他的程序效果同样很慢,自己初步尝试后放弃;
- 既然这样,干脆选择最简单的vector,最后进行去重,一开始无脑push_back计算出来的交点,最后操作一次,因为满足交点个数小于MAX=5000000,只要在超过MAX时就去重,这样最后在去重一次,就不会出现无脑push的导致重复点过多的问题。
包装vector.push_back()函数,添加后,若超过MAX,就排序去重,然后添加,最后全部计算完成后,再次排序去重,得到结果。性能截图如下,主要的热点就是排序去重的部分,占据76%左右,而set占据80%左右,好处是vector操作较为轻量级。总体时间节省不少。
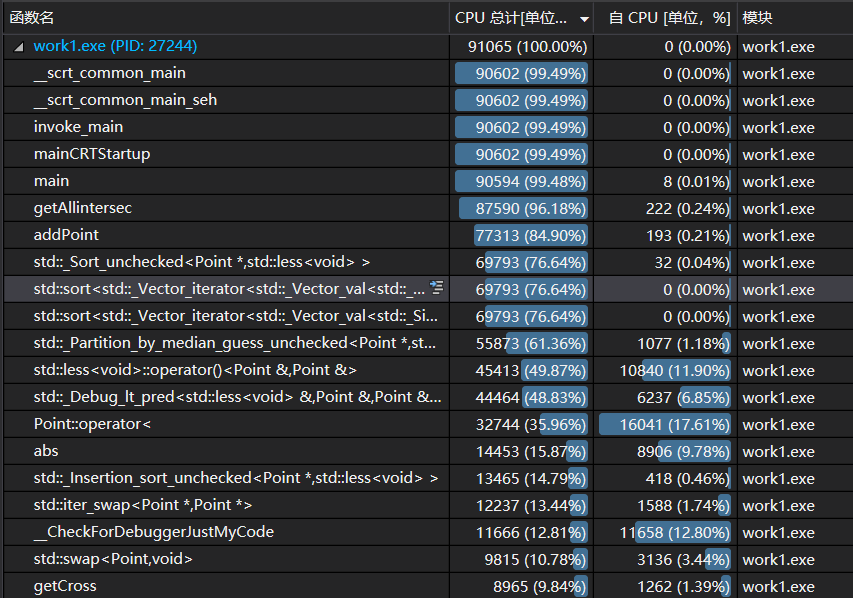
- 热点函数展示
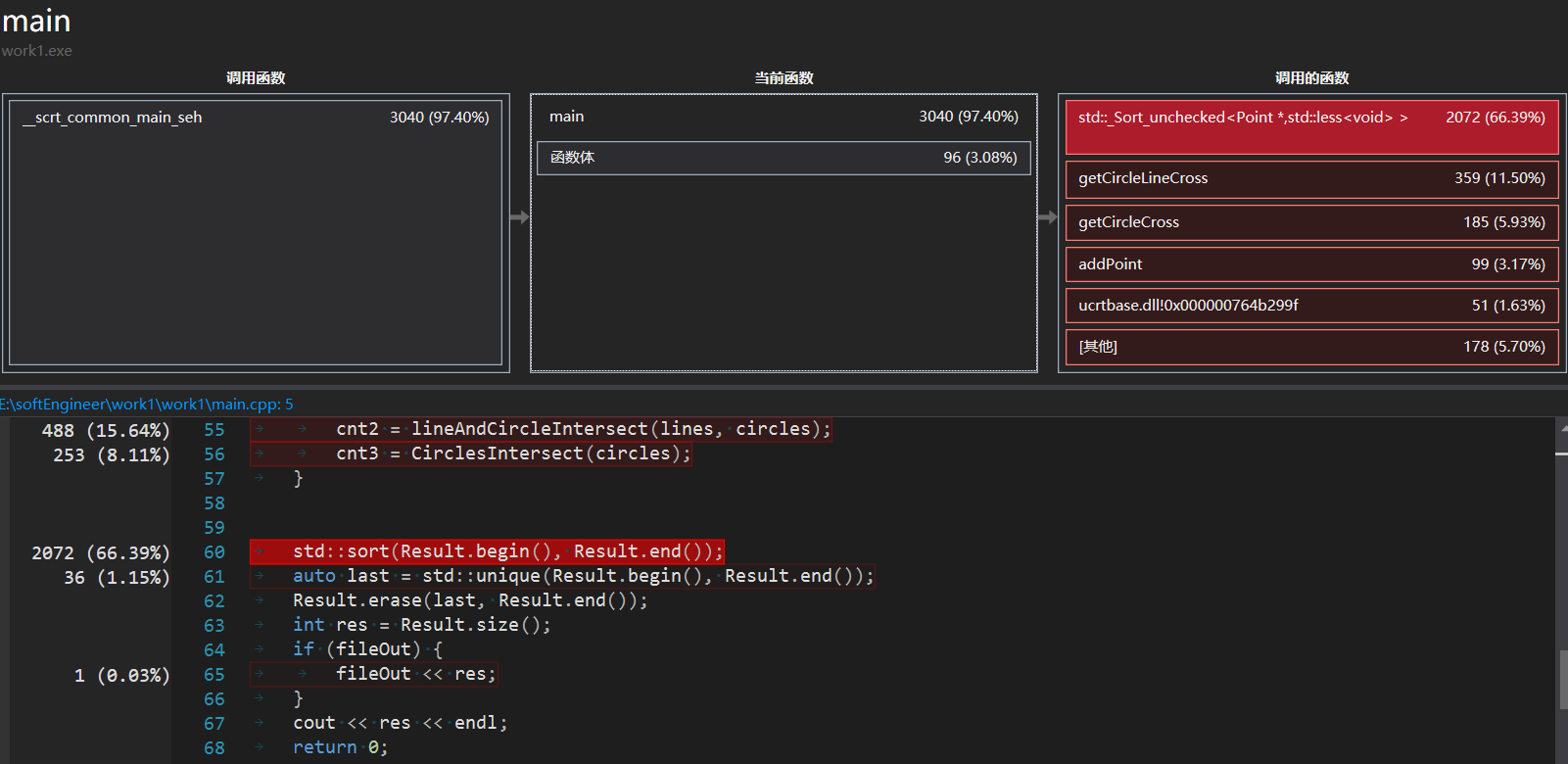
6. 代码说明。展示出项目关键代码,并解释思路与注释说明。(3')
-
直线和直线求交点:
采用前述的方法二计算,按照公式逻辑计算即可,只需要特判两直线是否平行即可。
//l1: a1*x + b1*y + c1 = 0 //l2: a2*x + b2*y + c2 = 0 //向量法求解: //D判断是否平行 //x0 = (b1 * c2 - b2 * c1) / D //y0 = (a2 * c1 - a1 * c2) / D bool getCross(Line l1, Line l2, Point* res) { //求l1的a1,b1,c1 double a1 = l1.getPy() - l1.getQy(); double b1 = l1.getQx() - l1.getPx(); double c1 = l1.getPx() * l1.getQy() - l1.getQx() * l1.getPy(); //求l2的a2,b2,c2 double a2 = l2.getPy() - l2.getQy(); double b2 = l2.getQx() - l2.getPx(); double c2 = l2.getPx() * l2.getQy() - l2.getQx() * l2.getPy(); double D = a1 * b2 - a2 * b1; //平行则退出,没有交点 if (D == 0) { return false; } res->setPoint((b1 * c2 - b2 * c1) / D, (a2 * c1 - a1 * c2) / D); return true; } -
直线和圆求交点:
- 先判断是否有交点
- 然后利用向量法求解
bool getCircleLineCross(Circle c, Line l) { Point ceter = c.getCeter(); double R = c.getR(); //求圆心到直线的距离 double juli = getDistance(l, ceter); //判断是否相交,或者相切,还是不相交 if (juli > R + PRECISION) { return false; } //求垂足的坐标 Vector segment = l.getQ() - l.getP(); double ratio = dot(ceter - l.getP(), segment) / segment.norm(); Point foot = l.getP() + segment * ratio; //特判,如果相切,则交点就是垂足坐标 if (abs(juli - R) < PRECISION) { addPoint(foot); return true; } //直线AB的单位向量,与AB同向 Vector e = segment / segment.module(); //base = 直线与圆相交的弦的一半. 利用勾股定理 double base = sqrt(R * R - (ceter - foot).norm()); //向量加减得到两个点的坐标 Point p1 = foot - e * base; Point p2 = foot + e * base; addPoint(p1); addPoint(p2); return true; } -
圆和圆求交点:
按照公式步骤求解,具体逻辑就是计算公式,不赘述。
bool getCircleCross(Point c1, double r1, Point c2, double r2) { double x1 = sqrt((c1 - c2).norm()); double b1 = abs(r1 - r2); double b2 = abs(r1 + r2); //判断相离,内离和外离 if (x1 < b1 || x1 > b2) { return false; } //外切 else if (x1 == b2) { Vector e = (c2 - c1) / (c2 - c1).module(); addPoint(c1 + e * r1); return true; } //内切 else if (x1 == b1) { Vector e = (c2 - c1) / (c2 - c1).module(); if (r1 < r2) { addPoint(c1 - e * r1); } else { addPoint(c1 + e * r1); } } //相交 else { Vector AB = (c2 - c1); double l = AB.module(); Vector e = AB / l; double AE = (r1 * r1 - r2 * r2 + l * l) / (2 * l); Point E = c1 + AB * AE / l; double CE = sqrt(r1 * r1 - AE * AE); //两圆心横坐标相同 if (c1.getX() == c2.getX()) { Point left(E.getX() - CE, E.getY()); Point right(E.getX() + CE, E.getY()); addPoint(left); addPoint(right); } //两个圆心纵坐标相同 else if (c1.getY() == c2.getY()) { Point up(E.getX(), E.getY() - CE); Point down(E.getX(), E.getY() + CE); addPoint(up); addPoint(down); } //一般情况 else { double k1 = (c2.getY() - c1.getY()) / (c2.getX() - c1.getX()); double k2 = -1 / k1; double EF = sqrt(CE * CE / (1 + k2 * k2)); double cx = E.getX() - EF; double cy = E.getY() + k2 * (cx - E.getX()); double dx = E.getX() + EF; double dy = E.getY() + k2 * (dx - E.getX()); Point tmp(cx, cy); addPoint(tmp); tmp.setPoint(dx, dy); addPoint(tmp); } } return true; }
7. 在你实现完程序之后,在下述 PSP 表格记录下你在程序的各个模块上实际花费的时间。(0.5')
| PSP2.1 | Personal Software Process Stage | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 60 | 60 |
| · Estimate | · 估计这个任务需要的时间 | ||
| Development | 开发 | 480 | 720 |
| · Analysis | · 需求分析 | 30 | 60 |
| · Design Spec | · 生成设计文档 | 30 | 30 |
| · Design Review | · 设计复审 | 30 | 15 |
| · Coding Standard | · 代码规范 | 30 | 15 |
| · Design | · 具体设计 | 60 | 60 |
| · Coding | · 具体编码 | 120 | 180 |
| · Code Review | · 代码复审 | 60 | 240 |
| · Test | · 测试 | 120 | 120 |
| Reporting | 报告 | 60 | 120 |
| · Test Report | · 测试报告 | 30 | 60 |
| · Size Measurement | · 计算工作量 | 15 | 30 |
| · Postmorten & Process Improvement Plan | · 事后总结,并提出过程改进计算 | 15 | 30 |
| 合计 | 600 | 900+ |
附录
Code Quality Analysis
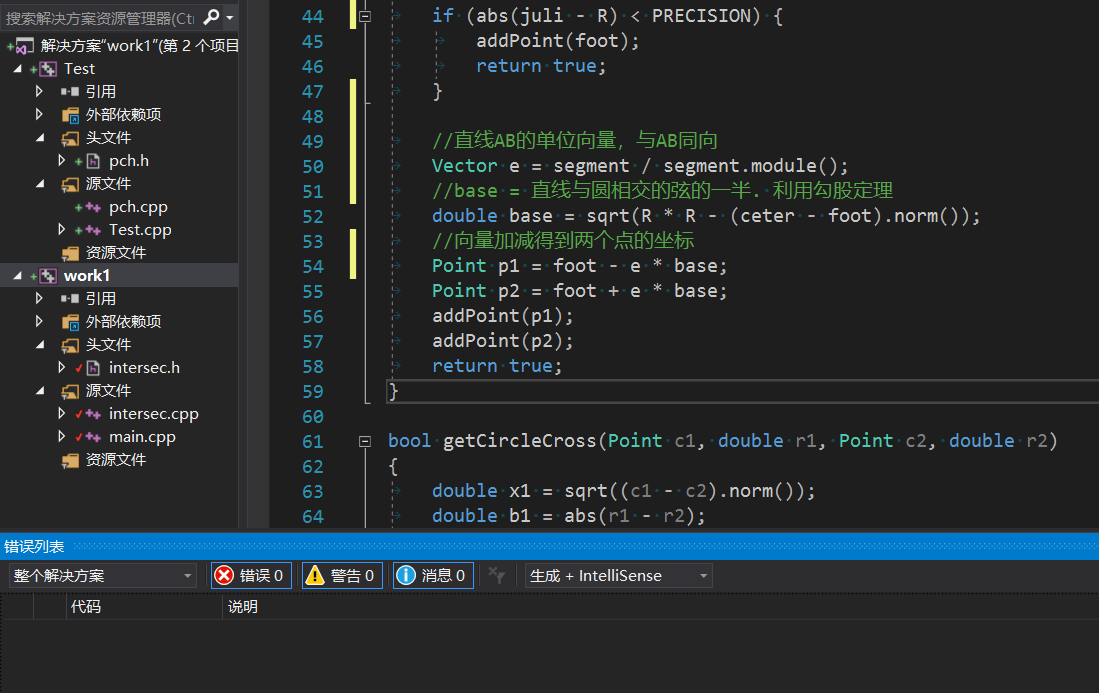


 浙公网安备 33010602011771号
浙公网安备 33010602011771号