论文阅读笔记-Topology Preserving Local Road Network Estimation from Single Onboard Camera Image

Topology Preserving Local Road Network Estimation from Single Onboard Camera Image

从单一的机载摄像机图像中进行拓扑结构保护的本地路网估算

Abstract

道路网络拓扑的知识对于自主规划和导航至关重要。然而，仅部分探索了从单个图像中恢复这种拓扑结构。此外，它还需要参考地平面，也就是在该地平面上执行驱动操作。本文旨在直接在鸟瞰图 (BEV) 中提取本地道路网络拓扑结构，所有这些都位于复杂的城市环境中。唯一的输入包括单个板载前视摄像头图像。我们使用一组有向车道曲线及其交互来表示道路拓扑，这些交互是使用它们的交叉点捕获的。为了更好地捕获拓扑，我们引入了最小循环（minimal cycles）及其覆盖（covers）的概念。最小循环是由有向曲线段（两个交点之间）形成的最小循环。封面是一组曲线，其分段参与形成最小循环。我们首先表明覆盖足以唯一地表示道路拓扑。然后使用覆盖物来监督深度神经网络，以及车道曲线监督。这些学习从单个输入图像预测道路拓扑。 NuScenes 和 Argoverse 基准测试的结果明显优于使用基线获得的结果。

1. Introduction

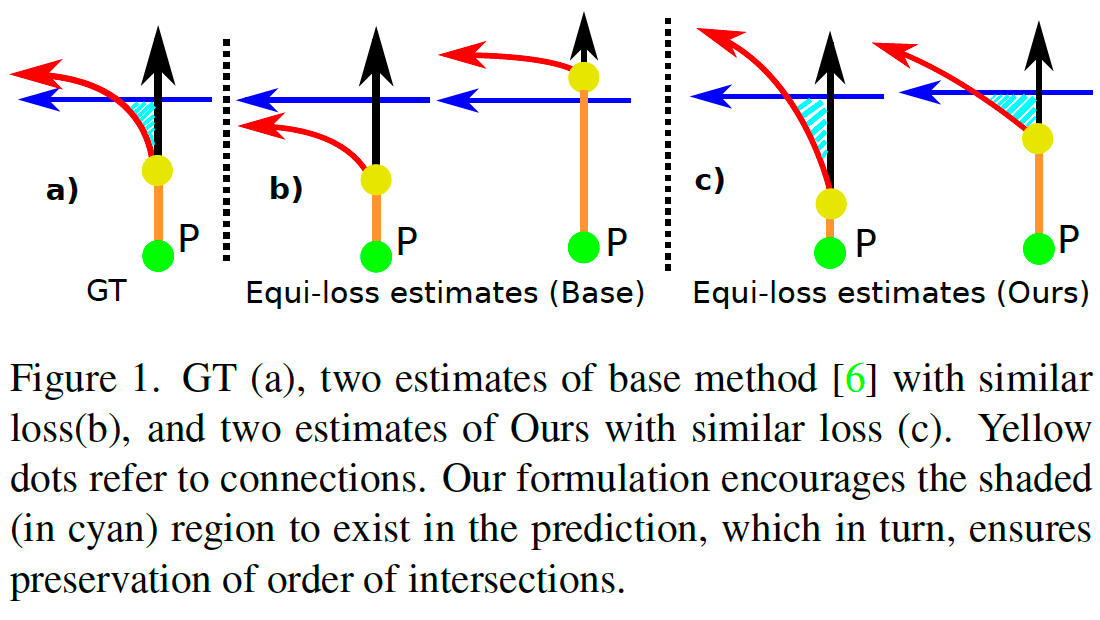
你会如何给司机指路？最直观的方法之一是说明转弯而不是距离。例如，第三个路口右转比直行 100 米右转更直观、更稳健。这一观察促使我们使用相关车道及其交叉口对道路网络进行建模。我们对按交通方向排序的车道交叉口进行建模。给定一条参考中心线 \(L\) 和两条与 \(L\) 相交的线 \(I_1\)、\(I_2\)，我们将在交点 \(L-I_1\) 和 \(L-I_2\) 之间与 \(L\) 相交的所有可能线的集合视为等价类。这种建模允许我们使用道路网络的拓扑结构明确地监督学习过程。反过来，推理过程中的拓扑一致性也得到了改善。考虑一辆汽车从图 1 中的绿点 \(P\) 向上移动，它需要先左转。在 [6] 的两个估计中，第一个左侧通向不同的车道。尽管底层有向图在所有估计中都具有相同的连通性，但它们具有非常不同的拓扑结构，这些拓扑结构在决策制定中起着重要作用。

对于自动驾驶，汽车周围的本地道路网络中包含的信息对于自动驾驶系统的决策至关重要。本地道路网络既用于预测其他代理的运动 [15、23、36、45]，也用于规划自我运动 [3、12]。表示道路网络的最流行方法是基于车道图的高清地图，其中包含有关中心线及其连通性的信息。大多数现有方法通过使用离线生成的高清地图结合模块化感知堆栈来解决道路网络提取问题[10、24、29、35、39]。然而，基于离线高清地图的解决方案有两个主要问题：（i）依赖于高清地图 [29、43] 中的精确定位，（ii）构建和维护此类地图的要求。这些要求严重限制了自动驾驶在地理受限区域运行的可扩展性。为了避免离线映射[6]，建议直接从一张车载图像在线估计本地道路网络。受这种方法的启发，并考虑到基于图的地图拓扑一致性的重要性，我们建议直接监督地图生成网络以估计拓扑一致的道路网络。

从 [6] 开始，我们使用一组贝塞尔曲线来表示当地的道路网络。每条曲线代表一条行驶车道，在起点和终点的帮助下沿着交通流定向。然而，与 [6] 相比，我们还考虑了由这些有向曲线及其交叉点建模的道路网络的拓扑结构。更准确地说，我们依赖于以下陈述： 如果每条车道与其他车道的交叉顺序保持不变，则保留道路网络的拓扑结构。 直接估计交叉点的顺序是一个难题。因此，我们引入了最小循环及其覆盖的概念。最小循环是由有向曲线段（两个交点之间）形成的最小循环。在图 2 中，每个最小循环由不同的颜色表示。覆盖是一组曲线，其分段参与形成最小循环。给定两组曲线（一组估计和一组基本事实），如果两组中的所有曲线以相同的顺序相交，则两组定义的拓扑是等价的。在这项工作中，我们表明可以通过比较最小循环的覆盖来测量这种等价性。根据我们的发现，我们监督深度神经网络，该网络学习从单个图像预测拓扑保留道路网络。据我们所知，这是第一项研究估计道路网络拓扑问题的工作，从而超越了传统的车道图。

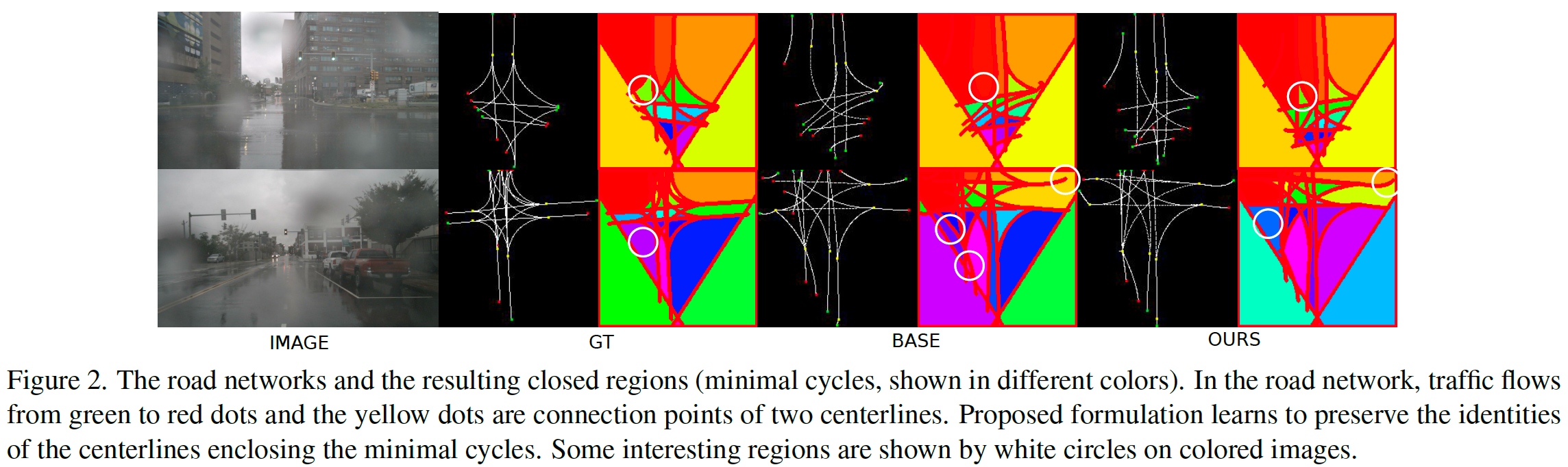
我们的模型预测车道曲线以及它们如何连接以及它们的覆盖物的最小循环。在学习过程中，曲线和循环都受到联合监督。曲线监督是通过匈牙利算法将预测曲线与地面实况匹配来执行的。类似地，循环监督将预测循环的覆盖与基本事实的覆盖相匹配。这种联合监督鼓励我们的模型在推理过程中预测准确和拓扑保持的道路网络，而不需要分支进行循环监督。

对于自动驾驶和其他机器人应用中的在线地图绘制，直接预测鸟瞰（BEV）中的道路网络至关重要，因为自动驾驶汽车的动作空间是地面。这与主要发生在图像平面中的传统场景理解形成对比。最近表明，在图像平面上执行 BEV 场景理解，然后将其投影到地平面上不如直接预测地平面上的输出 [7、9、33、34、38、42、43]。与我们的方法相比，这些方法不提供本地道路网络，而是在 BEV 上进行分割。请注意，仅道路区域并不能提供所需的拓扑信息。执行车道检测的类似方法仅限于像高速公路这样的道路，其中车道的拓扑结构很简单，并且无法预测具有交叉路口的城市场景中的道路网络，这是我们感兴趣的设置。如前所述，[6] 能够预测此类道路网络，但不考虑拓扑，我们将证明我们的拓扑推理可以改进 [6] 中提出的方法。

我们预测的连接曲线为我们提供了完整的车道图高清地图。

2. Related Works

现有作品可以大致分为两个不同的组；首先，离线方法，从航拍图像或聚合传感器数据中提取高清地图风格的道路网络。其次，在线方法，仅在给定当前车载传感器信息的情况下，估计车道边界或在 BEV 平面上执行语义理解。我们的方法位于两种方法之间，估计高清地图风格的车道图，然而，基于车载单目图像。

Road network extraction: 早期的道路网络提取工作使用航拍图像 [2, 37]。基于相同的设置，最近的工作 [4,40,41] 更有效地执行网络提取。基于航空成像的方法仅提供粗略的道路网络。这样的预测可能对路由有用，但是，它们对于行动计划来说不够准确。

High definition maps: 高清地图通常使用聚合的 2D 和 3D 视觉信息离线重建 [21,26,27]。尽管这些工作是我们工作的主要动机，但它们需要密集的 3D 点云来进行准确的高清地图重建。这些方法也是在某些规范帧中恢复高清地图的离线方法。

在许多情况下，使用恢复的地图需要准确的定位。与我们类似的工作是 [20]，其中以折线的形式在高速公路上检测车道边界。 [20] 的扩展使用 RNN 在 3D 点云中生成初始边界点。然后将这些初始点用作预测车道边界的 Polygon -RNN [1] 的种子。我们的方法与 [20] 的不同之处在于：（i）点云与单个图像输入，（ii）高速公路车道边界与不受限制的车道中心线。

Lane estimation: 在使用单目相机进行车道估计方面有相当多的研究 [17, 31]。该任务要么直接在图像平面 [18、25] 上执行，要么通过将图像投影到地平面 [16、31、44] 在 BEV 平面上执行。然而，这一研究方向主要集中在高速公路和乡村道路上，没有交叉路口。在这种情况下，生成的道路车道工作的拓扑通常是微不足道的，因为线不相交。我们的方法侧重于具有复杂道路网络的城市交通，其中拓扑结构是基础。

BEV understanding: 由于其实用性，BEV 上的视觉场景理解最近变得流行 [7, 34, 38]。一些方法还将图像与 LIDAR [19, 32] 相结合。也许与我们的方法最相似的是 [7,30,38]，它使用单个图像或单目视频帧进行 BEV 高清地图语义理解。但是，这些方法不提供结构化输出，因此它们在规划和导航方面的使用受到限制。

总之，在我们的论文中，我们在类似于 [22] 的设置中工作，其中输出是有向无环图。但是，输入不是聚合图像和 LIDAR 数据，而只是一张机载图像。因此，与现有车道估计相同的传感器设置可以工作，但是这些传感器并非设计用于在城市环境中工作。事实上，我们的设置与 [6] 相同，但我们的工作确实侧重于车道图的拓扑，并提出了一种直接监督网络以估计拓扑正确图的方法。

3. Method

3.1. Lane Graph Representation

在 [6] 之后，我们将本地道路网络表示为车道中心线段的有向图，通常称为车道图。设此有向图为 \(G(V, E)\)，其中 \(V\) 是图的顶点（中心线），边 \(E ⊆ \{(x, y) | (x, y) ∈ V ^2\}\) 表示这些中心线之间的连通性。连通性可以通过图 \(G(V, E)\) 的关联矩阵 \(A\) 来概括。一条中心线 \(x\) 连接到另一条中心线 \(y\)，即 \((x, y) ∈ E\) 当且仅当中心线 \(y\) 的起点与中心线 \(x\) 的终点相同。这意味着如果中心线 \(x\) 和 \(y\) 相连，则 \(A[x, y] = 1\)。我们用贝塞尔曲线表示中心线。

3.2. Topological Representation

虽然有向图构建了交通场景的抽象高级表示，但该图还引入了有关道路场景的基本拓扑属性。拓扑属性取决于中心线的交点，而车道图取决于中心线的连通性（连接由 \(G(V, E)\) 的关联矩阵定义，而两条曲线之间的交点在几何意义上定义。）。因此，考虑拓扑结构也提供了补充信息，我们可以使用这些信息来估计更好的表示。

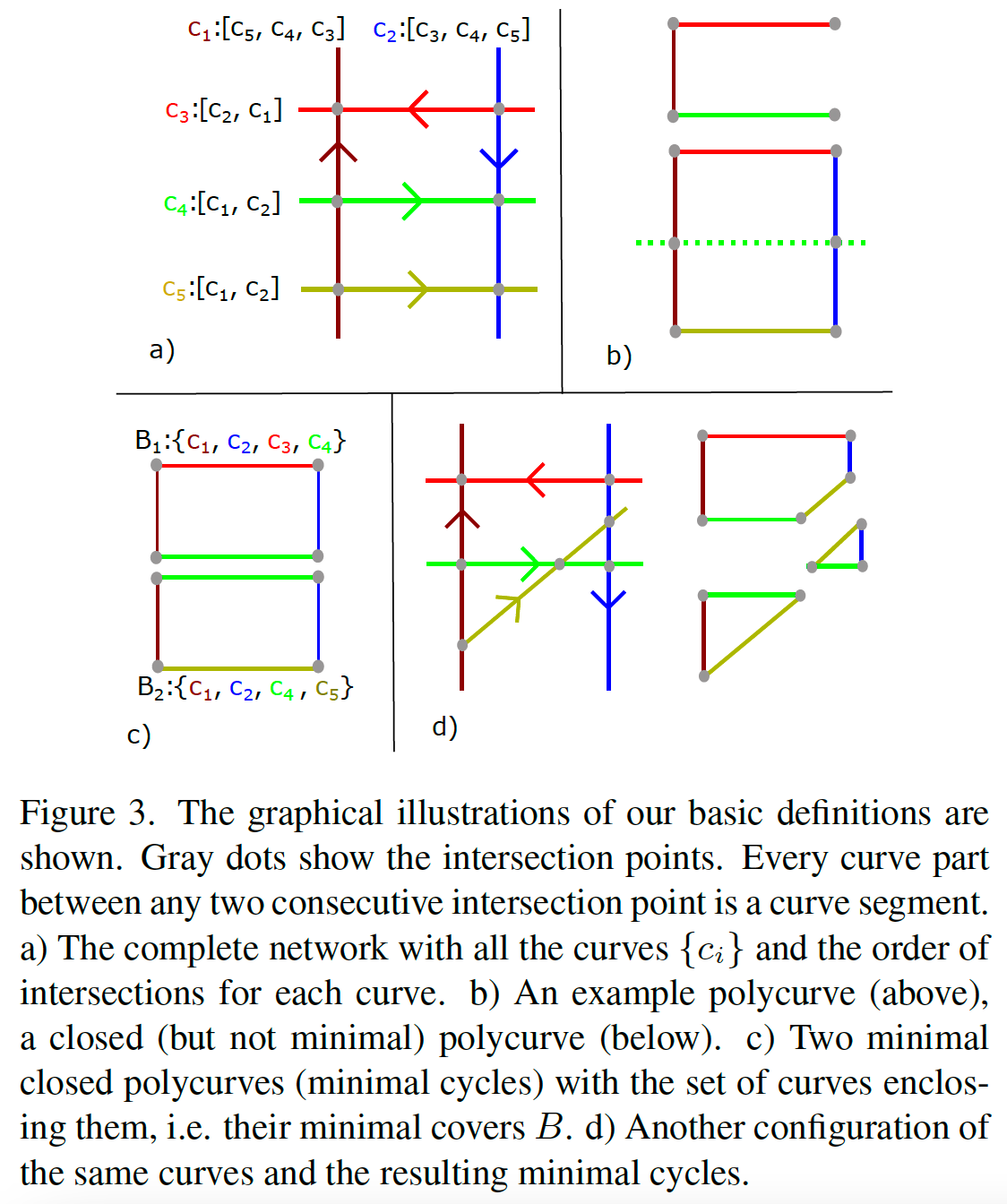
我们假设目标 BEV 区域是有界的 2D 欧几里得空间，其中已知的边界曲线表示视场 (FOV) 的边界。与车道图相同，每条曲线都有一个表示交通流量的方向，而边界曲线有任意方向。我们将包括边界曲线在内的所有曲线的集合表示为 \(C\)。为了建立我们以后的结果，我们假设任意两条曲线最多可以相交一次，并且一条曲线不与自身相交。由于受限的 FOV 和相对较短的曲线段，这个假设不是限制性的。此外，在车道图中，没有曲线是浮动的，因为曲线的每一端要么连接到另一条曲线，要么离开有界空间，这也会导致交叉点。令 \(c ∈ C\) 是一条曲线， \(I _c\) 是沿曲线 \(c\) 方向的有序交点序列， \(I_c(m) ∈ \mathbf{P}\) 是该序列的第 \(m\) 个交点，其中 \(\mathbf{P}\) 是所有交点的集合。所有曲线 \(c\) 的一组 \(I _c\) 用 \(I\) 表示。结合曲线 \(C\) 和交叉点顺序 \(I\)，我们可以形成我们的拓扑结构 \(T (C, I)\)，它与 \(G(V, E)\) 一起定义了当地的道路网络（参见图 3 a) ）。在这个线性曲线示例中，给出了所有曲线的交点顺序 \(I _c\)。

在估计交通场景的车道图，或者实际上是由曲线形成的任何图结构时，我们不仅希望正确估计车道图 \(G(V, E)\)，还希望正确估计拓扑属性 \(T(C, I)\)。然而，直接估计交点的顺序是非常具有挑战性的。在下文中，我们将证明在某些假设下，每条曲线的交点阶数 \(I_c\) 等价于曲线的最小循环的覆盖。这种等价性使我们能够有效地向我们的网络添加拓扑推理。让我们首先定义最小循环和覆盖。曲线段 \(S_c(i, j)\) 是连续交点 \(i\) 和 \(j\) 之间的曲线 \(c\) 的子集，由 \(I _c\) 可知。我们将多曲线 \(PC\) 定义为曲线段序列 \(PC _S = (S) _m|S _m(j) = S _{m+1}(i)\)。封闭的多曲线 \(CC\) 是没有端点的多曲线，它完全包围了一个区域（参见图 3 b) ）。最小闭合多曲线或最小循环 \(MC\) 是一条闭合多曲线，其中没有曲线与 \(MC\) 包围的区域相交，见图 3 c)。请注意，最小循环形成有界空间的分区。最后，给定一条形成 \(MC\) 的多曲线，我们还可以定义相应的最小覆盖 \(B\)，它是该多曲线中的线段所属的曲线的集合并集，或者换句话说，形成最小循环的曲线列表，参见图 3 c) 和 d)。最小覆盖 \(B\) 之所以如此有趣，是因为它们虽然相对简单，但我们将在下面展示它们仍然持有道路图的完整拓扑信息，并且等效于交叉点顺序 \(I\)。

为了建立这种等价性，让我们首先陈述以下结果，这些结果将交叉顺序与最小循环和覆盖联系起来，这在补充材料中详述的温和条件下成立。

Lemma（引理） 3.1. 一个最小闭合多曲线（最小循环） \(MC\) 由其最小覆盖 \(B\) 唯一标识。

\(Proof. 证明见补充材料。 \square\)

如果陈述是错误的，最小覆盖 \(B\) 的相同曲线 \(c _i\) 将需要生成另一个最小循环。在曲线只允许相交一次的假设下，这直观地变得困难。对于图 3 所示的线路，这是不可能的。对于一般曲线，证明变得更加复杂，需要一些进一步的假设，这些假设可以在补充部分中找到。

鉴于我们在最小覆盖和最小循环之间存在联系，我们现在关注交叉阶 \(I\) 和最小循环之间的关系。

Lemma 3.2. 让一组曲线 \(C_1\) 和诱导的相交阶数 \(I_1\) 形成结构 \(T_1 = (C_1, I_1)\)。对 \(C1\) 中的曲线应用任何变形（不包括删除或添加曲线）会产生一个新的诱导相交顺序，从而创建 \(T_2 = (C_2, I_2)\)。鉴于这两种类型，\(I_1 = I_2 \Longleftrightarrow MC_1 = MC_2\)。换句话说，当且仅当最小循环集相同时，两个结构的全局交集顺序相同。

\(Proof. 证明见补充材料。 \square\)

鉴于交叉顺序和最小周期之间的这种等价性，我们可以说明我们的主要结果。

Corollary（推论） 3.2.1. 从引理 3.1 和引理 11.2，给定结构 \(T = (C, I)\)，\(I\) 可以由最小覆盖集 \(B\) 唯一地描述。

关于推论 3.2.1 的显着事实是我们将全局排序问题转换为检测问题。无需为每条曲线创建序列，只需检测最小循环就足够了，其中每个最小循环可以由 \(T\) 中曲线的单热向量表示，该向量显示曲线是否在特定最小循环的最小覆盖范围内或不是。

3.3. Structural Mapping

先前的理论结果使我们能够训练一个联合估计曲线和相交顺序的深度神经网络。因此，我们为估计 \(T_E\) 和地面实况 \(T_T\) 结构建立曲线和最小覆盖之间的映射。

使用神经网络，我们预测固定数量的曲线和最小循环，这大于任何场景中的实际曲线和循环数。因此，假设有一个函数 \(U (x)\)，它接受输入 \(x\)（在我们的例子中是相机图像）并输出两个矩阵，大小为 \(N × D\) 的 \(V_c\)，它是所有 \(N\) 个曲线候选的 \(D\) 维嵌入；和大小为 \(M × E\) 的 \(V_m\)，这是所有 \(M\) 个最小循环候选的 \(E\) 维嵌入。两个嵌入矩阵均由函数 \(F (V_c)\) 和 \(H(V_m)\) 处理。 \(F (V_c)\) 处理嵌入 \(V_c\) 的曲线候选并生成一个矩阵输出 \(Z ^q _c ∈ \mathbb{R} ^{N×θ}\) 包含 \(N\) 条曲线的参数和 \(Z ^p _c ∈ \mathbb{R}^N\) 第 \(i\) 条曲线存在的概率。 \(H(V_m)\) 处理最小循环候选嵌入，并生成三个输出，每个输出描述最小循环的属性。首先，\(Z ^q _m ∈ \mathbb{R} ^{M×(N+K)}\)，\(M\) 个候选曲线中每一个的估计最小覆盖，描述了 \(N\) 条候选曲线和 \(K\) \(FOV\) 边界曲线之一属于覆盖的概率。其次，\(Z ^p _m ∈ \mathbb{R} ^M\) 存在候选最小循环的概率，最后，\(Z ^r _m(a) ∈ \mathbb{R} ^{M×2}\) 是估计候选最小循环中心的辅助输出。因此，我们的框架生成了一组曲线和最小循环候选，参见图 4 的说明。

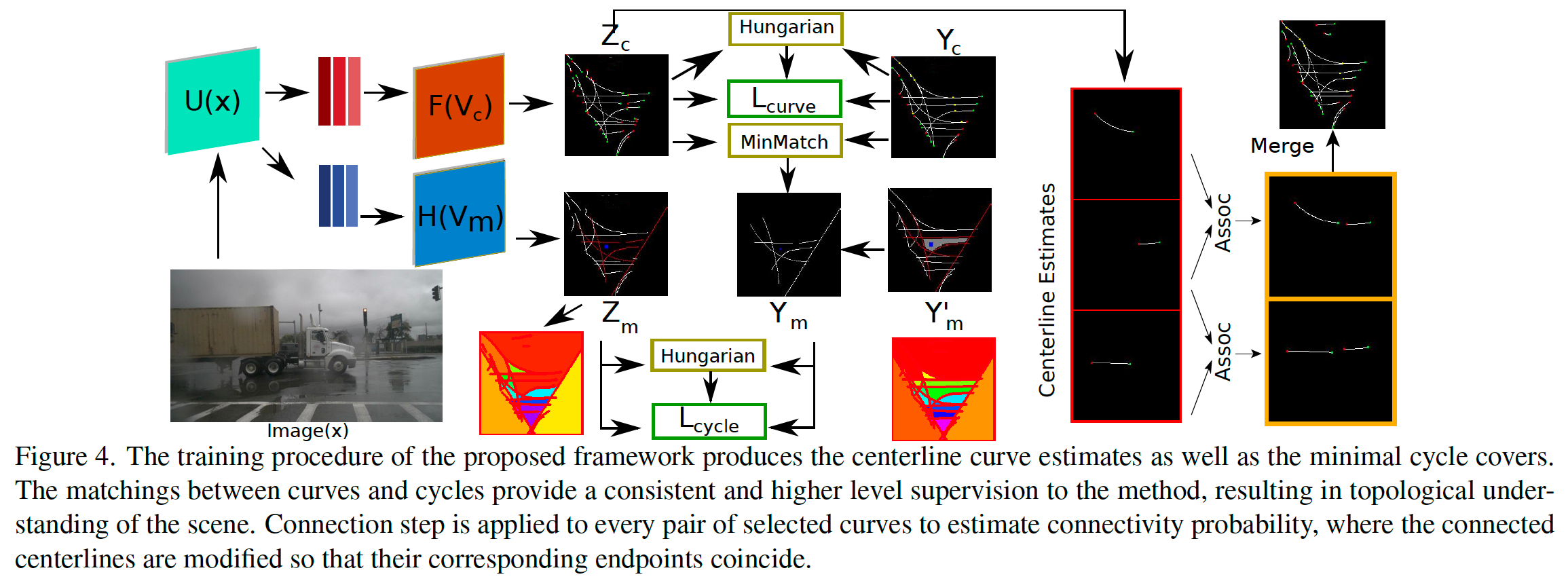
3.4. Training Framework

网络的输出是（i）一组候选曲线和（ii）关于候选曲线定义的最小循环。在训练中，我们对中心线控制点之间的 L1 差异使用匈牙利匹配。然而，对于最小周期来说，它更复杂，其中基本事实拓扑与估计拓扑之间的匹配是一致的。假设有 \(N '\) 条真曲线和 \(M '\) 条具有 \(K\) 条边界曲线的真正最小循环。类似地，\(Y ^{'q} _c ∈ \mathbb{R} ^{N'×θ}\) 表示真实曲线参数，\(Y ^{'q} _m ∈ \{0, 1\} ^{M'×(N'+K)}\) 表示相对于真实曲线的最小覆盖，\(Y ^r _m\) 表示真实中心的最小周期。

Min Matching. 由于在 GT 曲线上定义了基本事实 (GT) 最小循环，而在估计曲线上定义了检测到的最小循环，我们必须首先在估计曲线和 GT 曲线之间形成匹配。使用匈牙利匹配并不理想，因为它没有考虑估计曲线的碎片。碎片化是多条相连的估计曲线代表一条GT曲线的情况。因此，估计的候选最小循环通常比它们的 GT 对应物具有更多的候选曲线。由于匈牙利算法中的一对一匹配，一条长的 GT 曲线只能与一条短的、分段的曲线匹配，即使组合估计的分段会导致更接近的近似值。因此，我们改为将每条候选曲线与其最接近的 GT 曲线匹配。这意味着每条候选曲线都与一条 GT 曲线匹配，而一条 GT 曲线可以与任意数量（包括零）条候选曲线匹配。

在最小匹配之后，我们为最小循环估计创建了一个新目标，我们用 \(Y ^q _m ∈ \{0, 1\} ^{M'×(N+K)}\) 表示。如果与第 \(j\) 条估计曲线匹配的 GT 曲线在第 \(i\) 个真正的最小循环中，则 \(Y ^q _m(i, j)\) 中的条目为 1。换句话说，如果它们对应的真实曲线存在于最小周期中，我们将所有匹配的估计曲线设置为一条。给定这个修改后的 GT 最小循环标签和估计的最小循环，我们运行匈牙利匹配来找到用于损失计算的对。这允许对估计的拓扑进行一致的训练。

对于曲线的连通性，我们明确地估计了我们网络中 \(V (G, E)\) 的关联矩阵 \(A\)。这是通过为每个候选中心线提取一个特征向量并构建一个分类器 \(\hat{A}(C_i, C_j)\) 来完成的，该分类器采用属于曲线 \(C_i\) 和 \(C_j\) 的两个特征向量并输出它们的关联概率。训练使用匈牙利匹配曲线来建立正确的顺序。估计的关联矩阵允许在测试期间合并后处理步骤，其中曲线的端点被修改，以便连接的曲线重合。

中心线样条控制点和最小循环中心是用 L1 损失训练的，而我们利用二元交叉熵来计算中心线和最小循环概率。我们还将二元交叉熵用于最小循环的成员损失，即在 \(Z ^q _m\) 和 \(Y ^q _m\) 之间以及用于连通性。然后总损失变为 \(L = L_{curve} + α L_{cycle}\)，其中 \(L_{curve} = L_{splines}+β_e L_{exists}+β_c L_{connect}\)，并且 \(L_{cycle} = L_{member} + β_d L_{exists} + β_f L_{center}\)，具有 \(α\) 和 \(β_x\) 超参数。

4. Network Architectures

在 [6] 之后，我们专注于两种不同的架构来验证我们的公式的影响。第一种架构基于 Transformer [8]，而第二种方法基于 Polygon-RNN [1]。

4.1. Transformer

我们修改了 [6] 中提出的基于 transformer 的架构。我们使用两种类型的学习查询向量：中心线（曲线）和循环查询。在由转换器处理之前，我们连接中心线和循环查询。因此，曲线和周期是联合估计的。转换器输出处理后的查询，对应于我们公式中的 \(V_c\) 和 \(V_m\)。最后，我们将这些向量通过两层 MLPs 以产生估计 \(Z_c\) 和 \(Z_m\)。图 5 给出了概述。请注意，添加 MC 公式会添加可忽略的参数，因为变压器中的参数数量是固定的。我们将带有 MC 的变压器模型称为 Ours/TR。

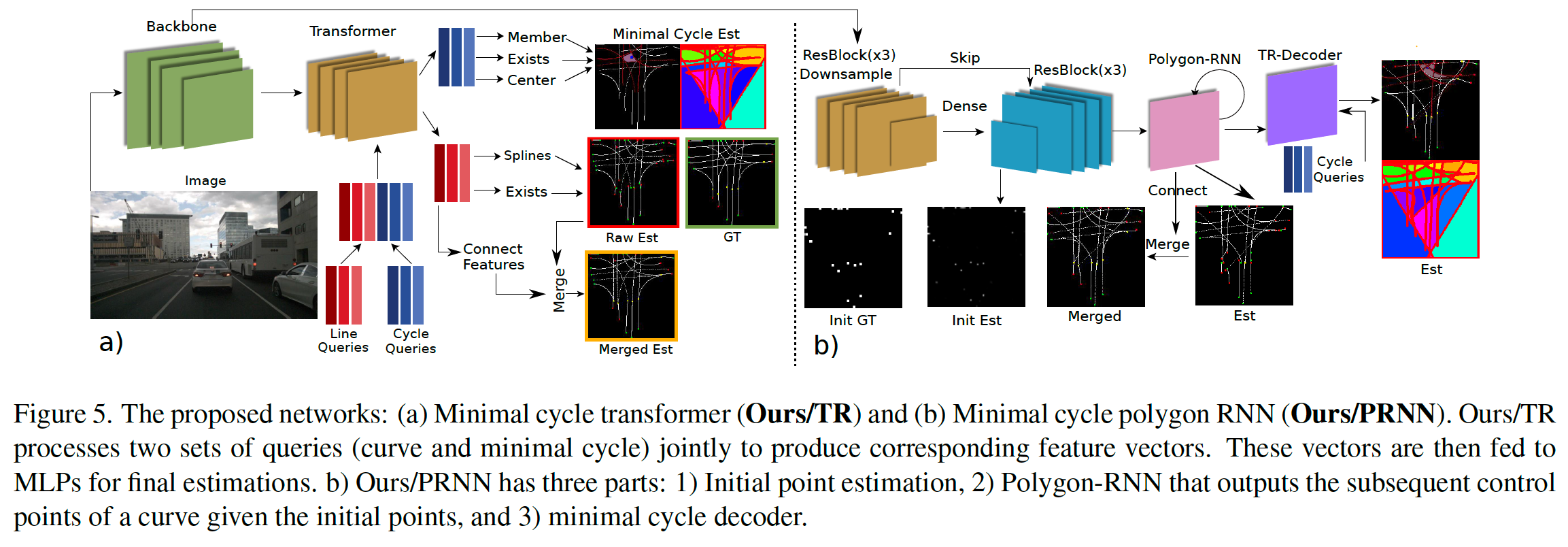
作为基线，我们在基础 transformer 上添加了一个 RNN，以直接估计交叉点的顺序并为网络提供监督。 RNN 独立处理来自转换器的每个中心线查询输出，并在每个时间步生成一个 \(N + K + 1\) 维向量，表示 \(N + K\) 曲线之一与一个“结束”标记相交的概率分布。 RNN 由通过匈牙利匹配转换为估计中心线的真实相交顺序进行监督。我们将这种方法命名为 TR-RNN，详情参见 Suppl.Mat. 。

4.2. Polygon-RNN

第二个网络基于 Polygon-RNN [1]，类似于 [20]，作者从点云生成车道边界。我们调整 [20] 以处理图像并输出中心线而不是车道边界。在 [6] 之后，我们使用了一个以 \(V_c\) 为输入并输出一个网格的全连接子网络。每个元素表示从该位置开始的曲线的初始曲线点的概率，即 \(Z ^p _c\)。

给定初始位置和主干特征，Polygon-RNN [1] 生成中心线的下一个控制点。我们将 Polygon-RNN 的迭代次数固定为用于编码中心线的样条系数的数量。到目前为止描述的方法形成了基础 Polygon-RNN 。使用 Polygon-RNN 产生 \(Z ^q _c\) ，我们在架构中添加了一个变压器解码器来检测最小周期。我们使用一组类似于我们的转换器架构的最小循环查询，其中查询使用 Polygon-RNN 的最终特征图进行处理。因此，在 transformer 解码器中，查询向量参与整个估计中心线集以提取最小循环候选。对于这个过程，我们将 RNN 状态填充到固定大小并添加位置编码。这确保了解码器接收到关于曲线身份的信息。处理后的查询向量被传递给与转换器架构中相同的 MLPs，以产生一组最小周期估计 \(Z_m\)。图 5 概述了这种方法，我们称之为 Ours/PRNN。与基于变压器的方法不同，这是一个两阶段的过程，首先估计中心线，然后估计最小周期。

5. Metrics

[6] 中提出了几个指标来衡量估计车道图的准确性。它们是 M-F-Score 、检测率 和 连通性 。这些指标不涵盖道路网络的拓扑结构。因此，我们提出了两个新的指标来捕捉估计拓扑的准确性。建议的指标补充了现有的车道图指标，以全面了解估计的道路网络的准确性。

Minimal-Cycle Minimal Cover (B). 我们测量 2 个输入的最小循环精度。首先，从估计中提取最小周期。我们使用第 3.4 节的过程来获得 \(Y ^q _m\)。然后，使用匈牙利匹配来匹配这些循环以计算真阳性、真阴性和假阳性。这个度量被称为 MC-F。我们还测量了最小循环网络的准确性。与 MC-F 类似，首先获得 \(Y ^q _m\)，然后我们阈值 \(Z ^p _m\) 以获得检测到的 \(Z ^q _m\)。然后，我们应用匈牙利匹配并计算匹配循环的统计数据。我们将此度量称为 H-GT-F，仅在检测到最小周期时才适用。 H-GT-F 测量 MC-network 在估计真实拓扑中的真实循环时的性能。最后，H-EST-F 测量 MC-head 在检测估计周期方面的性能。由于提取的 MCs 和 MC head 估计是关于估计曲线的，我们直接对提取和估计的 MCs 运行匈牙利匹配。

Intersection Order (I of G(C, I)). 为了衡量方法在保留交集顺序方面的性能，我们从最小匹配开始。然后对于每条真实曲线，我们选择最接近的匹配估计。对于给定的真实曲线 \(C_i\)，让匹配曲线为 \(S_i\)。我们从 \(C_i\) 和 \(S_i\) 中提取交叉点的顺序，并在它们之间应用 Levenshtein 编辑距离。然后通过真实曲线的交点数对距离进行归一化。我们将此指标称为 I-Order。

6. Experiments

我们使用 NuScenes [5] 和 Argoverse [11] 数据集。两个数据集都以中心线的形式提供高清地图。我们将中心线的世界坐标转换为当前帧的相机坐标系，然后使用目标 BEV 分辨率重新采样这些点，并丢弃感兴趣区域 (ROI) 之外的任何点。然后使用 ROI 边界 \([0, 1]^2\) 对这些点进行归一化。我们为这个归一化坐标系提取贝塞尔曲线的控制点。该方法的基本事实和估计值也在同一坐标系中表示。我们使用 [38] 中提出的相同训练/验证拆分。

Implementation. 我们使用尺寸为 448x800 的图像，目标 BEV 区域在 \(x\) 方向从 -25 到 25m，在 \(z\) 方向从 1 到 50m，分辨率为 25cm。由于中心线的复杂性有限，使用了三个 Bezier 控制点。我们为中心线和最小循环使用两组 100 个查询向量：一组用于右侧（Boston & Argoverse），一组用于左侧交通（Singapore）。主干网络是在 Cityscapes 数据集 [14] 上预训练的 Deeplab v3+ [13]。我们的实现在 Pytorch 中运行，以 11 FPS 运行，没有批处理，包括所有关联步骤。在训练 Polygon-RNN 时，我们使用真正的初始点来训练 RNN，遵循 [20]。为了训练初始点子网络，我们使用了焦点损失[28]。

Baselines. 我们与 [6] 中提出的基于最先进的 transformer 和基于 Polygon-RNN 的方法以及使用方法 PINET [25] 提取车道边界的另一个基线进行比较。然后使用地面实况变换将提取的车道边界投影到 BEV 上。然后我们耦合成对的车道边界并使用样条线提取中心线。不评估此基线的连通性。

7. Results

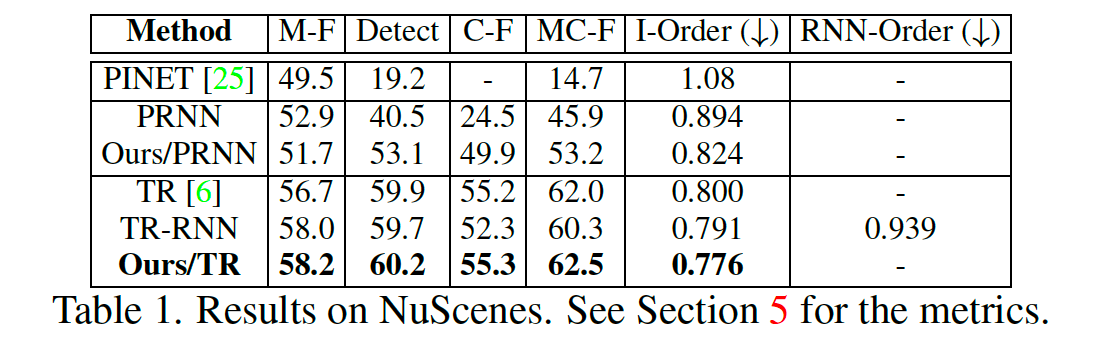
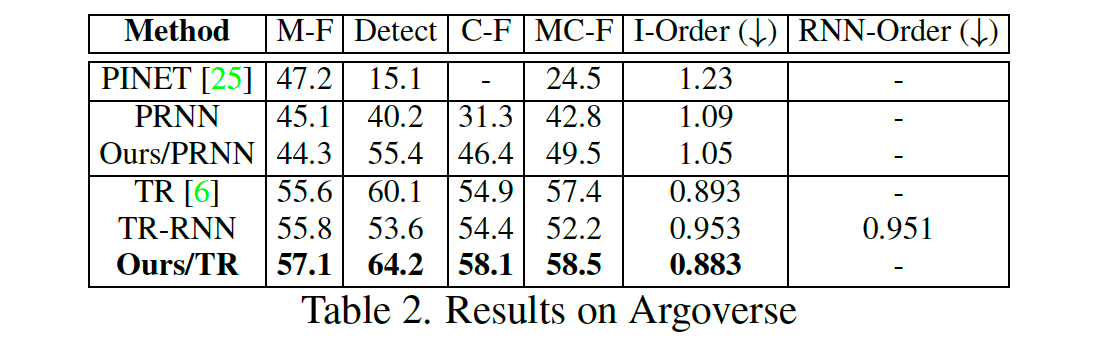
我们在表 1 中报告了Nuscenes 数据集上与 SOTA 的定量比较。提出的公式为基于 Polygon-RNN 的方法提供了几乎所有度量的实质性提升。与 [6] 中提出的基于 transformer 的方法相比，我们的方法在所有指标上都表现得更好。我们还在表 2 中的 Argoverse 数据集中验证了我们的方法。可以看出，我们的方法始终优于竞争对手。

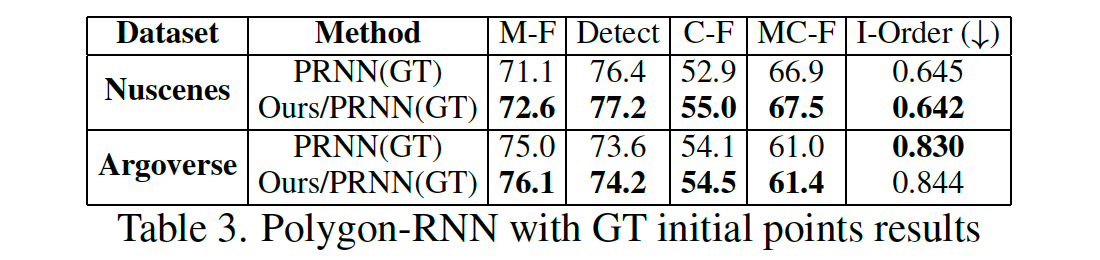
我们还报告了表3中给定真实初始中心线点的基于 Polygon-RNN 的方法的结果。请注意，Polygon-RNN 和 Polygon-RNN(GT) 是具有相同参数的相同模型，唯一的区别是真实或估计的初始点。结果表明，我们的公式适用于显著不同的架构和不同的设置。

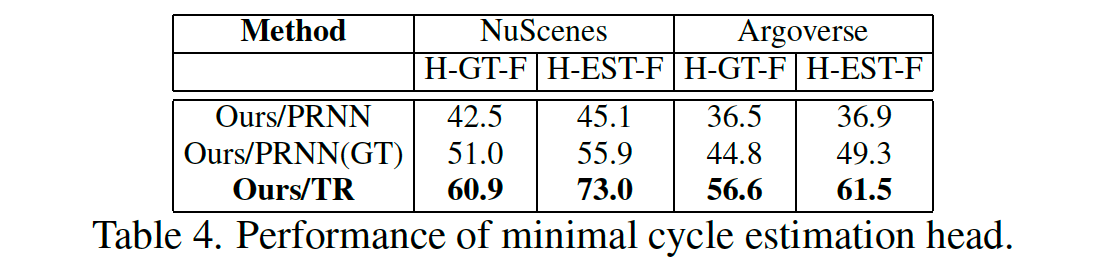
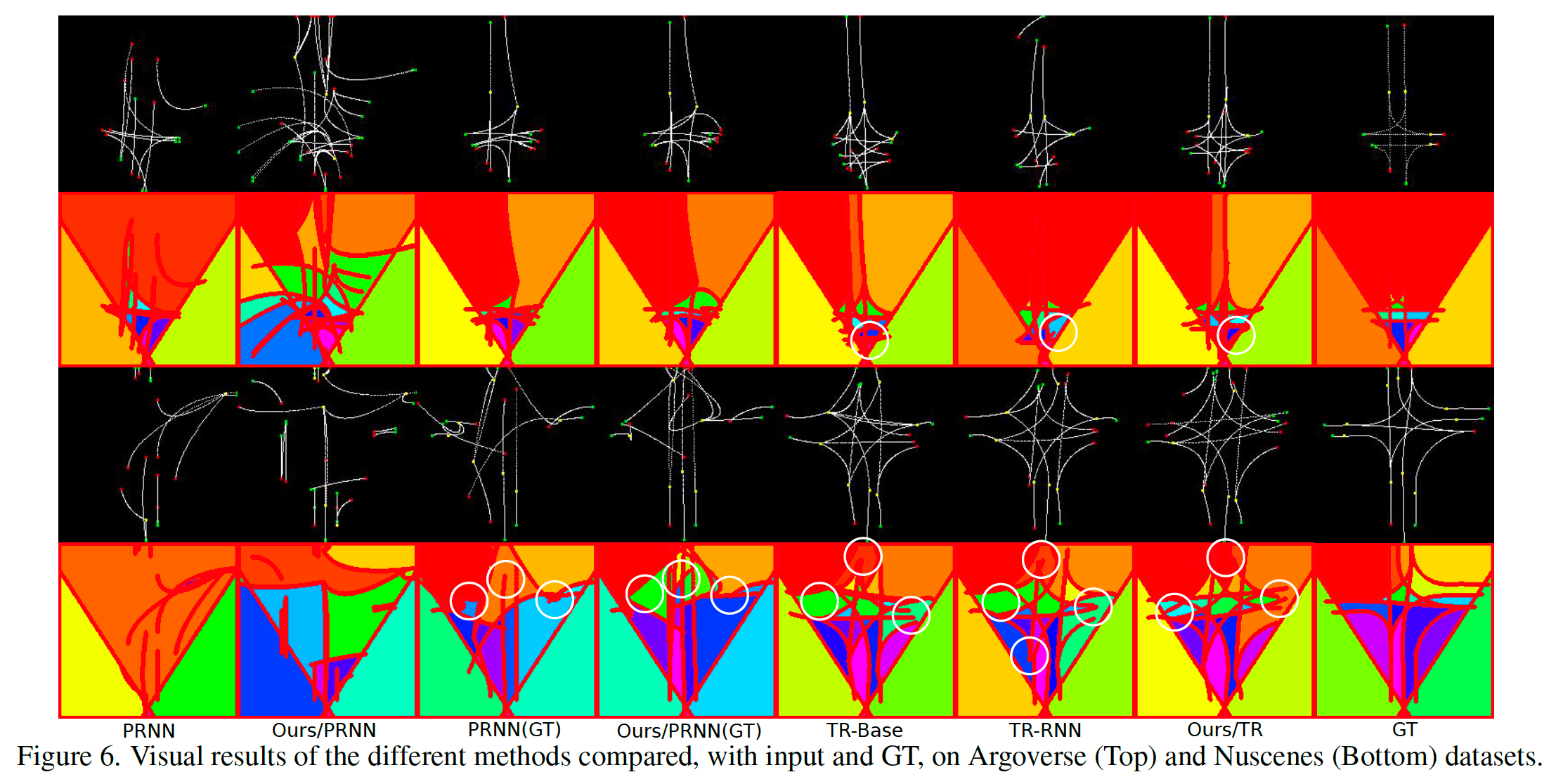
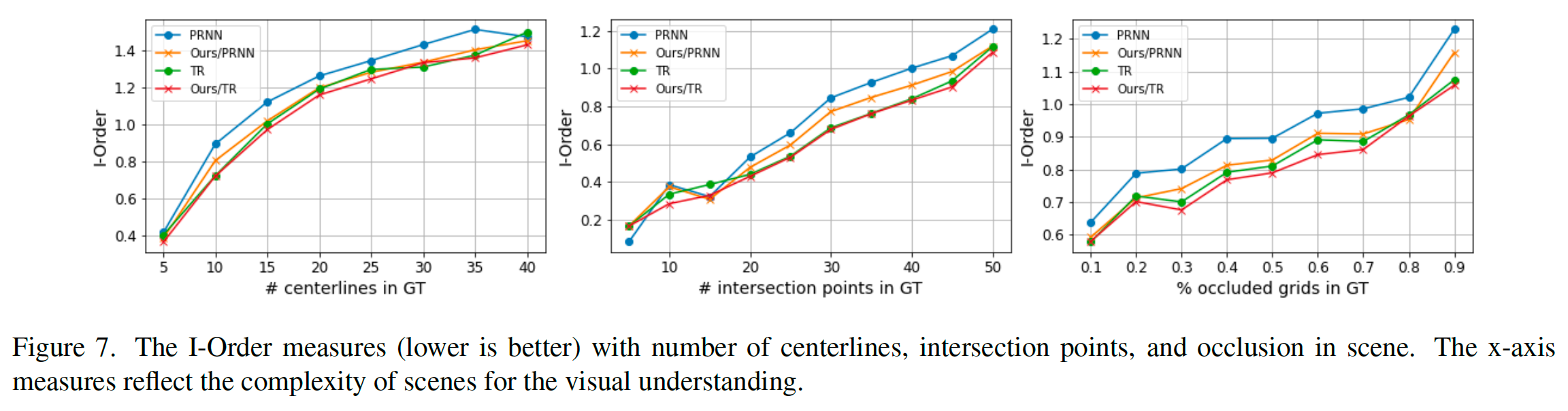
远非其真正实现的编辑距离。这表明交叉点的递归估计是我们在表 4 中提供了对建议的最小循环分支的评估。两个数据集中的 H-GT-F 结果表明，基于变压器的方法在检测真正的最小周期方面更好，因此可以估计真正的拓扑。此外，从 H-EST-F 结果可以看出，基于 transformer 的方法更能自我感知得到的路网估计。从 transformer 的 H-GT-F 和 MC-F 值之间的相似性可以得出相同的结论。这意味着该方法输出的中心线估计与其拓扑估计一致。这些结果是预期的，因为变压器联合估计中心线和最小周期，而 Polygon-RNN 输出是分阶段的。一个重要的观察结果是 MC 度量与 I-Order 有明显的相关性，经验证明 MC 覆盖和相交顺序的等价性。我们观察到 TR-RNN 方法的直接阶估计不如我们基于最小循环的公式准确。在 Nuscenes 数据集中，随着场景复杂度增加，不同方法的性能如图 7 所示。正如预期的那样，随着中心线、交叉点和场景遮挡数量的增加，所有方法的性能都会下降。尽管如此，所提出的基于 MC 的方法始终能产生比基线更好的 I-Order。比较方法的一些定性示例如图 6 所示，其中使用 MC 分支的方法再次更可取。

8. Conclusion

我们研究了从单个车载摄像头图像中提取本地道路网络。为了鼓励拓扑一致性，我们通过仅匹配它们的覆盖来制定最小循环匹配策略。然后我们的公式被用来推导损失，训练两种不同架构的神经网络，即 Transformer 和 Poly-RNN。两种架构都在两个常用的基准数据集上展示了所提出的 MC 分支的重要性，以及由此形成的损失函数。所提出的公式和方法有可能用于许多其他需要拓扑一致输出的计算机视觉问题，例如室内房间布局估计或场景解析。

Limitations. 对于大多数现代道路网络，理论假设是温和的。提取训练的最小周期非常耗时，应该离线完成。