论文阅读笔记-MapLite: Autonomous Navigation in Rural Environments without Detailed Prior Maps

MapLite: Autonomous Navigation in Rural Environments without Detailed Prior Maps

MappLite：在没有详细的预先地图的农村环境中的自主导航

方法概述：

• 首先，我们使用车载传感器分割场景，以检测前方的道路。输入是一个3D点云，分割步骤为每个点产生一个标签，以表明它是在道路上还是在道路外。
• 接下来，我们进行拓扑配准，以使OpenStreetMap (OSM)与观测到的场景最匹配。在这里，输入是来自OSM的拓扑地图，配准步骤在不改变地图拓扑的情况下，对输入地图进行变形，以更好地匹配道路分割的输出地图。
• 最后，在拓扑层次上解决导航问题，在度量层次上解决路径规划问题，生成局部目标路径。
  • 这需要首先使用A*解决拓扑图上的最短路径图搜索问题，
  • 然后使用结果路径作为应用安全约束(如留在道路上)的变分规划器的参考。其结果是一个包含高级导航信息和本地规划约束的引用路径。
  • 最后，使用纯追踪控制器跟踪这条路径，该控制器生成正确的转向角度，从而沿着参考路径到达目标。动态速度控制器控制车辆的速度，以确保它不违反最大速度或加速度限制。

这里的基本思想是对小规模定位使用局部感知，对全局定位和导航使用拓扑感知。

在这项工作中，我们利用了这样一个事实，即在驾驶环境中，已经存在一个策划和开放的拓扑图。

MapLite系统

框架概述

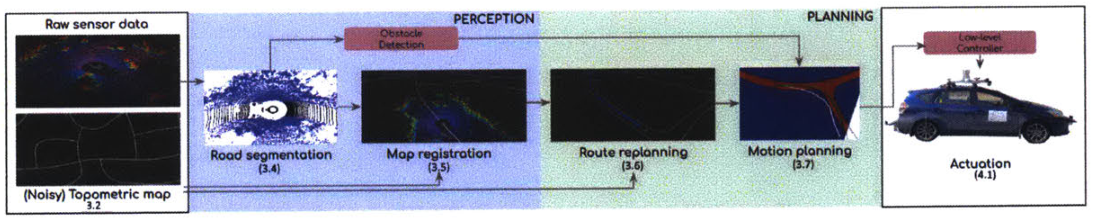
MapLite系统与典型的自主导航管道不同的五个部分:拓扑图、道路分割、地图注册、路线重新规划和运动规划。

地形图

我们的方法只需要一个地形图，它不包含精确定位所需的细节。地形图在MapLite系统中起着至关重要的作用。在这里，我们简要地描述它的结构以及它与通常使用的高清晰度地图的不同之处。

地形图是简单的类图数据结构，其扩展是每个节点都与地球表面上由经度和纬度描述的二维点相关联。我们利用UTM变换的平坦地球近似，它将顶点放置在一个平面上。因此对于每一张地图M，我们都有 \(M=\{V,E\}\) ，其中每个顶点 \(v_i \in{\mathbb{R}^2}\) 描述一个路径点，每个边 \(e_i\in{E}\subset{|V|\times|V|}\) 描述一个路段。然而，虽然可以假定网络的连通性是相对正确的，但具体航路点的相对精度或全局精度却不能这样说。

基本实例：单边遍历

首先设计并实现了一个在没有岔路和路口的地方的自主导航。在此应用中，将整个感知和规划模块被替换为单个组件，该组件直接从传感器输入和OSM映射到底层控制器。我们通过检测道路边界并使用它们直接估计必要的控制命令来实现这一点。

基本实例的算法概述如下：

用激光扫描仪不断产生点云数据。提出了一种获取车辆传感带内道路边界点的算法。然后用RANSAC/最小二乘方法拟合这些点，在道路边界点内获得最优轨迹。重要的是，拟合的质量也从最小二乘最小化的剩余输出得到。这使得轨迹估计在下一次迭代中被概率地融合。车辆还配备了里程数传感器，用于在车辆移动后将先前的轨迹估计传播到当地的车辆框架。

因此，参考轨迹始终在车辆局部坐标系内。由于里程数的更新速度通常比传感器到达的速度快得多(在这种情况下为100Hz)，所以即使没有收到新的里程数，车辆也可以继续遵循参考轨迹一段时间。最后，利用参考轨迹引导车辆朝向局部目标进行边缘遍历。

序言

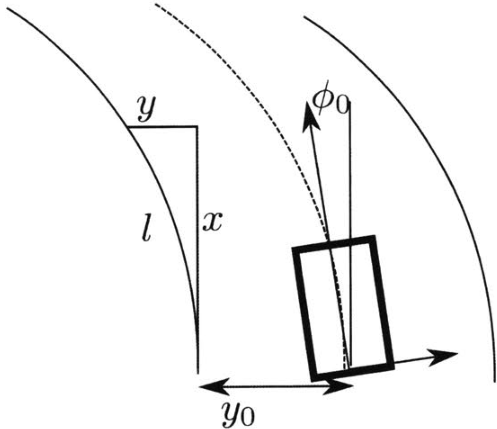
通常将参考轨迹表示为一个回旋曲线。具体来说，我们选择将道路建模为一度的回旋线，道路的曲率线性变化。我们可以通过对路径曲率积分来恢复路径上的方向。并基于微分几何，在笛卡尔坐标系中重新参数化回旋线：

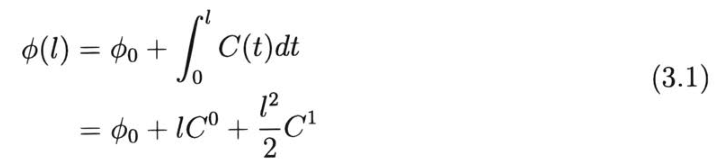
基于微分几何，我们可以在笛卡尔坐标[20]中重新参数化回旋线:

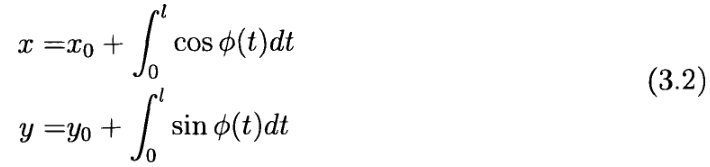
假设:(a)曲线在笛卡尔坐标下的原点与车辆 \((x_0 = 0)\) 一致，(b)曲线在行进过程中的航向变化相对较小 \((\cos \phi (t) \thickapprox 1, \sin \phi (t) \thickapprox \phi(t) \forall t)\) ，我们可以得到如下笛卡尔坐标下的样条表示:

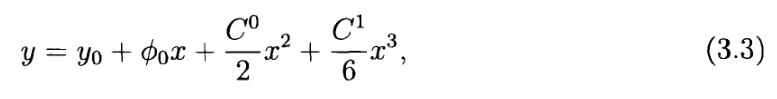
边缘遍历

将时刻 \(t\) 时机器人的局部坐标系定义为 \(X_t\) ；
在拓扑地图中遵守 \(e_{ij}\) 边道路规则的有效构型集定义为 \(\mathcal{X}_{ij}\) ；
在时刻 \(t\) 时传感器条带定义为 \(S_t\) ；
本节中假设 \(\mathcal{X}_{ij}\) 为 2D ，即道路段近似平坦。

接下来，我们寻找局部目标是 \(X_t\) 中尽可能接近（在欧几里得意义上）\(v_j\) 的点，图顶点列表中的下一个路点为：

\[(x_{goal},y_{goal})=\mathop{\arg\min}\limits_{(x_t,y_t)\in{S_t\cap\mathcal{X}_{ij} }}||^{X_t}v_j-[x_t,y_t]^T||_2 \tag{3.4} \]

其中 \(^{X_t}v_j\) 是顶点 \(v_j\) 在\(X_t\)坐标系中的笛卡尔坐标。

这个公式解释了两种重要的可能性，这是由于我们在本地框架中进行规划的事实：

• 1)OSM地图中的GPS坐标可能不够准确，精确导航到这些坐标将是危险的；
• 2)图中下一个到达的顶点可能足够远，它可能在车辆的传感器带之外。

在这种情况下，不可能生成一个可行的参考路径，从当前的车辆位置一直到下一个路径点。我们通过将目标航路点投影到传感器条带的可行空间来解决这两个问题。

因此，参考轨迹满足: $$\tau (\alpha) : [0,1] \mapsto \mathcal{X} _{ij} $$其中，\(\tau(0)=[0,0]^T\)，\(\tau(1)=[x _{goal},x _{goal}]^T\)

一般情况下，该轨迹可以用弧长或曲率在内部参数化;然而，我们将假设存在一些M到笛卡尔坐标的映射:

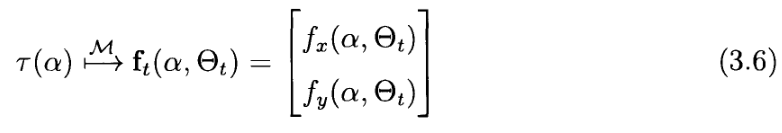
其中 \(f(\alpha, \Theta)\)定义了用来表示轨迹的模型， \(\Theta\) 是递归估计的模型参数。此外，由于参考轨迹是使用有噪声的传感器数据生成的，我们还得到了 \(\sigma _\tau(\alpha)\)，它包含了沿 \(\alpha =[0,1]\) 方向上每个点的相关不确定性。

(3.1) 和 (3.2) 结合起来，使用 (3.3) 中的样条参数化定义 (3.6) 中的映射 M，方法是根据以下公式选择 \(f(\alpha, \Theta)\)

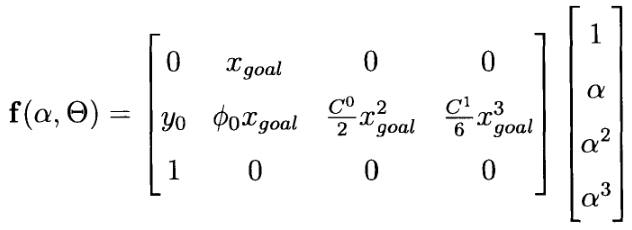
我们将用来估计传感器条带内允许配置的四维状态将是： \(\mathcal{S} _t \cap \mathcal{X}_{ij} = \{y_0, \phi_0 , C ^0 , C ^1\}\) 。 请注意，该区域是当前传感器条带中的最大可行驶区域， \(\mathcal{X}_{ij}\) 中的道路约束规则可用于进一步限制道路特定部分的允许轨迹。 在此应用中，由于道路位于没有迎面而来的车辆的测试设施中，因此选择轨迹以跟随道路的中心。

来自里程计的轨迹传播

我们使用了一个零滑移运动学里程数运动模型来建模车辆的运动。假设我们获得了位置线性向前变化的噪声测量 \(\Delta _x + \epsilon _x\) ，以及航向变化的噪声测量 \(\Delta _\phi + \epsilon _\phi\) 。然后给出了运动学模型:$$x ^r _{t+1}=x ^r _t+(\Delta _x + \epsilon _x)\cos \phi ^r _t$$$$y ^r _{t+1}=y ^r _t+(\Delta _x + \epsilon _x)\sin \phi ^r _t$$$$\phi ^r _{t+1}=\phi ^r _t+(\Delta _\phi + \epsilon ^r _\phi)$$其中， \(X ^r = [x ^r _\phi,y ^r _\phi,\epsilon ^r _\phi] ^T\) 是车辆在时刻t时的姿态。

我们在每个时间步将“全局参考系”与局部参考系重新对齐。也就是说令 \(x ^r _\phi = y ^r _\phi = \epsilon ^r _\phi = 0\) ，运动模型可以明显简化:$$x ^r _{t+1}=(\Delta _x + \epsilon _x)$$$$y ^r _{t+1}= 0$$$$\phi ^r _{t+1}=(\Delta _\phi + \epsilon ^r _\phi)$$

我们更新了局部参考框架，使其与车架相吻合。定义测量为 \((\Delta _x, \Delta _\phi)\) ，其不确定度为 \(\sigma _\Delta\) 。这是通过一个标准齐次变换矩阵来实现的，\([\bar{x} _{t+1} , \bar{y} _{t+1} ,1] ^T = \mathbf{T} ^{-1}[x _t, Y _t, 1] ^T\)：其中$$\mathbf{T}=\left[ \begin{array}{c}
\cos (\Delta _\phi) & - \sin (\Delta _\phi) & \Delta _x \\
\sin (\Delta _\phi) & \cos(\Delta _\phi) & 0 \\
0 & 0 & 1 \\
\end{array}
\right]$$

然后，如果将映射 \(\mathcal{M}\) 限定为一个线性函数，其模型参数为 \(\mathbf{f}(\alpha,\Theta)= \Theta \mathbf{A}(\alpha)\) ，则新坐标系下的模型参数为:

\[\begin{align*} \bar{x} _{t+1} & = \mathbf{T} ^{-1} x _t \\ & = \mathbf{T} ^{-1} f(\alpha,\Theta _t) \\ & = \mathbf{T} ^{-1} \Theta _t \mathbf{A}(\alpha) \\ & = \bar{\Theta} _{t+1} \mathbf{A}(\alpha) \end{align*}\]

其中 \(\bar{\Theta} _{t+1} = \mathbf{T} ^{-1} \Theta _t\) ，将参照系变化引起的修正传播到参数上，以保持 \(\mathbf{f}\) 的固定模型形式。

在实践中，这个测程回路的频率比下一小节中描述的测量回路快得多。

当新的车辆里程计到达时，估计的样条被更新。 过程模型由下式给出:$$X ^s _{t+1}=f(X ^s _t , X ^r _{t+1} , \epsilon _t)$$其中 \(\epsilon _t = [\epsilon ^x,\epsilon ^\phi,\epsilon ^{C ^0} , \epsilon ^{C ^1}]\) 是过程模型中所有加性零均值高斯噪声源， \(f\) 是通过将里程计公式中更新的车辆估计值代入样条函数公式得出的，并且合并由里程计产生的航向变化，这会导致在 \(\phi _0\) 参数中添加一个额外的偏移量：

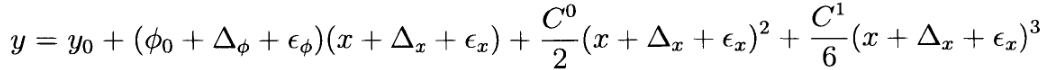
求解后，相对于相应项收集系数，得到无噪声过程模型:

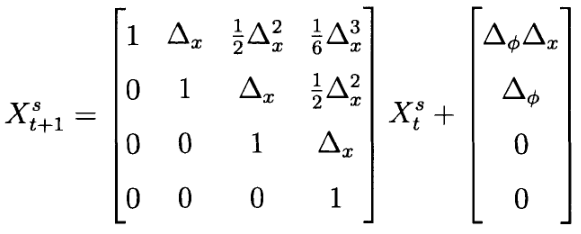
注意，这个过程模型对状态是线性的，而不是对噪声参数。因此，在预测阶段的每个时间步长计算噪声雅可比矩阵 \(W = \frac{\partial f}{\partial \epsilon _t}\):

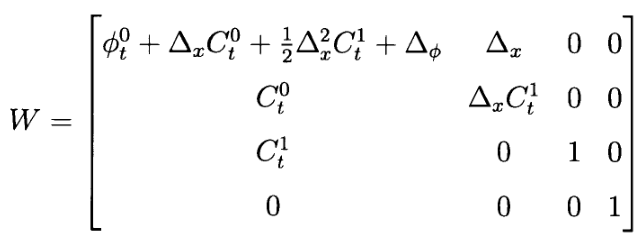
滤波器更新中最后的加性噪声项由 \(W^TQW\) 给出，其中 \(Q\) 是每个噪声源的噪声协方差的对角矩阵。

单次扫描道路边界检测

激光雷达传感器中，每个激光扫描一圈，就会生成一个强度（传感器到目标的距离）曲线，将他展示在以角度为横坐标的坐标系中就可以清晰地分辨出道路位置。由于路面相对平坦，所以相对周围区域有更平滑的纹理，并且每个扫描环在位置上的变化也比其他位置（路边的草地或树）小。将这个信号处理后，选择一个阈值来调节灵敏度（这样可以灵活的处理不同的天气状况），进而搜索道路边缘。

一旦找到单次扫描得到的边缘，算法就会转向下一个环。边缘位置的猜测都选择与前一个环中欧几里得距离最短的点。这样道路边缘的检测就可以沿着道路的边缘逐步移动，而不需要探索距离道路较远的点云区域。

来自新局部估计的轨迹更新

使用RANSAC将边界点拟合到样条上(每条道路边界对应一条)。两条边界样条的平均值生成参考样条轨迹。每一次扫描曲线拟合的结果都被视为一次新的进给测量。RANSAC后，利用最小二乘拟合程序对样条进行内嵌拟合，并利用该拟合程序的残差来衡量测量更新的协方差。$$z_t=HX^s_t+\eta_t$$其中，\(H = [x,\frac{1}{2} x ^2, \frac{1}{6}x^3]^T\)，用于拟合曲线的每个数据点都可以看作是一个独立的测量值。对于点 i :$$ \eta ^i _t = || z ^i _t - H ^i X ^s _t||^2$$因此，使用检测到的道路来生成可行的驾驶轨迹，以及确定该轨迹是正确的度量。

由于感知系统普遍不完善，感知产生的不确定性可以传播到轨迹参数上。因此，我们得到了一个新的局部参考轨迹，\(f _{k+1}(\alpha，\hat{\Theta} _{k+1})\) ，在这里预定义的模型再次被拟合，轨迹的不确定性被传播到参数中。最后，由于测程传播的轨迹 \(f _{k+1}(\alpha，\bar{\Theta} _{k+1})\) 和传感器测量产生的新轨迹 \(f _{k+1}(\alpha，\hat{\Theta} _{k+1})\) 在同一局域参考系中，它们可以概率融合。

轨迹跟踪控制器

实现自主边缘遍历的最后一步是轨迹跟踪控制器。这将从估计的道路边界生成低水平的控制设定值。轨迹跟随器以沿道路参数化的轨迹样条作为输入，确定车辆沿该轨迹所应采取的转向角。由于轨迹生成总是发生在与车辆一致的框架中，所以我们使用移动目标点方法，即车辆总是在输入轨迹上以固定距离跟随一个点。

路面分割

将点云中的每个点都被标记为道路（road）或非道路（not road）。

上一节中使用的边界点检测方法足以完成简单的边缘遍历任务。然而，由于交点的边缘点不能直接映射到所需轨迹，因此不能用于完成导航任务。在本节中，我们描述了一种通用的道路表面分割算法，它可以直接分割点云中的所有点，甚至包括道路交叉口的点。我们使用线性支持向量机模型进行路面分割，因为它的运行速度非常快，精度接近cnn，并且在速度上进行实时操作。

我们的线性支持向量机依赖于从激光雷达数据中提取的五个特征：

• 由传感器直接测量的仰角z。
• 表面纹理的量度。
  • 它是对邻域 \(N_p\) 中的所有点 \(p_i\) 使用滑动窗口计算得到的。然后使用$$v_p=\frac{1}{|N_p|}\sum_{i\in{N_p}}|P_i-\bar{P}|^2$$计算每个点的局部方差 \(v_p\) ，其中 \(\bar{P}\) 是是 \(N_p\) 中所有点的均值。
  • 这一特征产生了一种局部表面纹理的测量方法，对于粗糙表面(如草地和树木)来说，该方法更大，而对于可行驶表面则更小。
• 每次返回的强度。用来考虑道路表面反射率的差异。
• 唯一的激光ID。用于解释HDL-64传感器中每个发射器的物理差异。激光识别包括在训练中，以解释单个设备中发射器之间的系统偏差。因此，如果切换到新的传感器，就需要收集新的训练数据。
• {0,1}中的指示器特性用于指示没有返回的任何点。这是很重要的，因为超出范围值的存在(太远或太近)包含有价值的分割信息。

这五个特征一起被用来将每个点归类为道路或非道路。

地形配准

这一步骤的目标是仅使用里程数测量和激光雷达扫描来获得机器人在地图上的位置的估计。该问题被表述为一个极大后验(MAP)估计问题，我们描述了其每个单独组件的计算和逼近。形式上，我们的目标是获得估计

\[\hat{x}_t=\mathop{\arg\min}\limits_{x_t}(-\ln P(x_t|Z^o_{1:t},Z^L_{1:t})) \]

其中， \(x_t = [x_t, y_t, \theta_t]\) 为机器人在时刻 \(t\) 时在拓扑映射框中的姿态， \(Z^o_{1:t}\) 和 \(Z^L_{1:t}\) 分别为截止时刻 \(t\) 的所有测程（odometry）和激光雷达（LiDAR）测量的集合。为了实现实时操作，需要这种可能性的近似值。

似然近似

使用贝叶斯规则，上式中的概率可以用其先验、LiDAR 观测似然和基于里程计的状态预测来表示。

\[P(x_t|Z^o_{1:t},Z^L_{1:t})\varpropto_x P(Z^L_t|x_t)\cdot P(x_t|\hat{x}_{t-1},Z^o_t) \]

其中第一个因素表示可能性，第二个因素表示先验。

激光雷达观测似然 \(P(Z^L_t|x_t)\)

每个LiDAR扫描 \(Z^L_t\) 表示为 n 个3元组 \(z_i = (l_i^L, y_i^L, l_i)\) 的集合，其中\(l_i^L, y_i^L\in{\mathbb{R}}\) 表示每个测量到的LiDAR点在传感器帧中的位置，\(l_i\)是前面所述分割模块中得到的一个二值分类标签。我们定义了有符号的距离函数 \(f_D (z_i, x_t, M)\) ，表示从点 \(z_i\) 到拓扑地图 \(M\) 上任意边上最近的点的距离(假设车辆位于位置 \(x_t\) )。我们使用 sigmoid 函数来模拟 \(x_t\) 位置上每个点 \(z_i\) 的观测概率

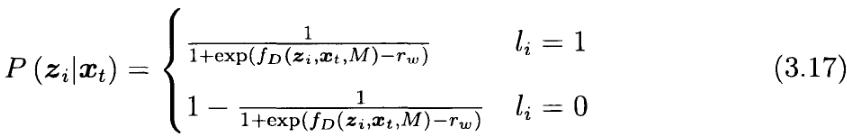
其中 r 是一个可调参数，表示找到标记为 road 的点的可能性，距离包含道路中心线的地图M很远。注意，在道路中心 \(f_D(z_i,M)=0\)，当远离道路的时候，若 \(l=1\) 则\(P(z_i) \thickapprox 1\)，若\(l=0\) 则\(P(z_i) \thickapprox 0\)，反之亦然。

本研究中 r 取常数即可。

最后，将整个激光雷达扫描的总体概率计算为单个测量元组的概率乘积\(P(Z^L_t|x_t)=\prod_i(z_i|x_t)\)。

基于里程计的预测 \(P(x_t|\hat{x}_{t-1},Z^o_t)\)

每个关于前一个姿态的里程数测量\(Z^o_t=[\Delta x_t,\Delta y_t,\Delta \theta _t]\)是通过使用扩展卡尔曼滤波器融合车轮编码器信息和IMU测量。基于里程数的未来状态的可能性被建模为

\[P(x_y|\hat{x}_{t-1},Z^o_t)\varpropto_x\exp(-\frac{||x_t-\hat{x}_{t-1}+Z^o_t||}{b}) \]

由于计算原因，比例因子b是通过参数调整得到的，而不是通过先验估计得到的。

实时操作的实现

计算成本的主要剩余驱动因素是评估 \(P(Z^L_t|x_t)\) 。这是由于\(f_D(^oz_i,M)\in O(|E|)\)（其中 \(|E|\) 是 M 中的边数），因此 \(P(Z^L_t|x_t)\in O(n\cdot |E|)\) 。为了实现加速，我们采用了一些进一步的近似方法。

• 首先，我们将包含映射 M 的空间离散化为大小为 \(r_c\) （实验中为0.5m）的单元格，并预先计算距离变换。对于每个地图，这种计算只需要进行一次，并且在实践中，对于大小为 \(1km^2\) 的地图，需要使用 \(<1s\) 。
• 接下来，我们使用两个可调参数\(s\in N_+,b\in [0,1]\)对输入的激光雷达扫描进行随机子采样，其中 s 是采样点的数量， b 是来自道路的期望点份额(即，\(l_i=1\)处)，以解释高度标签不平衡。
• 最后对(3.17)进行近似化简：$$(1+\exp(f_D(z_i,x_t,M)-r_w))^{-1}\thickapprox 1-\min(\frac{f_D(z_i,x_t,M)}{r_w},1)$$

在实践中，我们发现这些近似对系统性能的影响可以忽略不计，而在使用Intel i7处理器的标准笔记本电脑上，解决问题所需的时间从10秒减少到20毫秒。

路线规划

路线规划器负责选择从车辆起始位置到目标的最短路径。

• 输入：注册的地形图
• 输出：转换为图形结构并计算欧几里得距离作为边权重
• Next A* [24] 用于规划从起点到目标的最短路径。

其他模块需要大量计算，所以无法承受高频的重新计算整个路线。而且地形配准经常更新地图，也不能简单地重复使用原路线。为了解决这个问题，我们使用了一种 fast_update 方法，该方法在度量空间中更新路径中路径点的位置，而无需重新规划拓扑空间中的路径。此外，由于车辆可能会偏离计划的路径（例如，如果地图注册最近没有更新），我们还会检查与计划的偏差，并仅在必要时使用 A* 算法重新规划。下面算法描述了快速重新规划器如何确定何时需要重新规划路线规划或简单地快速更新现有路径到新地图。在我们的测试中，我们发现这将路线规划模块的平均延迟从 100 毫秒降低到了 1.5 毫秒。

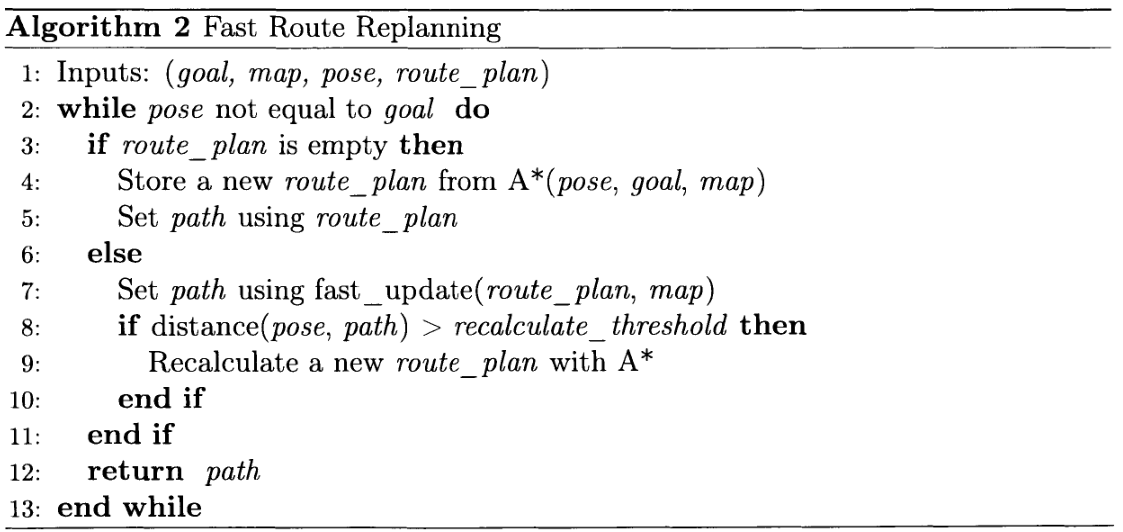
此外，我们利用有限状态机(Finite State Machine)将整个路线规划分解为子任务(例如，行驶到下一个路口)，使车辆能够等待目标、行驶、在每个路口做出正确的导航选择，并最终在目标目的地停车。

轨迹规划

轨迹规划器生成车辆到达目的地时必须遵循的轨迹。

• 输入：
  • 分段 LiDAR 扫描（Road egmention模块，该规划器集成从路线规划器获得的高级导航信息，以在传感器框架中规划局部安全路径。）
  • 来自 Route Planner 的高级导航参考路径
• 输出：利用变分轨迹规划器来生成安全轨迹。

地形配准和路线规划模块的结果虽然可以可靠地提供导航信息，但我们不能假设它在公制级别上是精确的，因为地形图确实不包含这样的细节。轨迹规划的路线是可靠的，因为它安全地留在路上，同时也达到了高水平的导航要求。

变分轨迹规划器利用 B 样条（B-splines） 参数化平滑轨迹。对于给定的参考轨迹 r，规划器完成两阶段的优化过程。

• 第一阶段：局部目标点选择包括确定与高层导航目标最近的点，该点既在车辆视场内，又位于路面上。
• 第二阶段：轨迹优化是基于短时间内描述的多个因素，寻找从当前车辆位置到目标点的“最优”路径。

局部目标点选择
参考路径首先被裁剪到传感器范围 \(\mathcal{X} \in \mathbb{R}^2\) 。然后，对于由 n 个路径点组成的参考路径r，我们将最终点表示为 \(r_n\) 。注意，虽然 \(r_n\) 的构建是在传感器范围内，它可能不位于路上。为了获得局部目标点，我们定义了一个代价函数 \(J(x)=[d(x),d_e(x,r_n)]\) 对于\(x\in \mathcal{X}\) ，其中\(d(x)\) 是 x 到 \(\mathcal{X}\) 空间的有符号距离函数， \(d_e(x,r_n)\) 是 x 到 \(r_n\) 的欧氏距离。那么目标点是由$$x_g=\arg \mathop{\min}\limits_{x\in \mathcal{X}}J(x)W^T_g$$构建的，其中 \(W_g\) 是一个权重向量，用于调整成本函数项的相对重要性。

轨迹优化
变化规划器的第二阶段创建一个 B 样条轨迹，该轨迹从车辆位置开始，到目标点 \(x_g\) 结束。 该优化利用由道路距离成本组成的三部分成本函数:$$J_d(\mathbf{q})=\frac{1}{k} \sum^{k}_{i=1} d(q_i)^2$$其中 \(\mathbf{q}\) 是具有 k 个路径点的候选 b 样条曲线，\(d(q_i)\)仍是到路径点的符号距离函数。

其次，为了保证较短的路径优先于同样可行的较长的路径，计算相对路径长度代价为：$$J_l(\mathbf{q})=\frac{\sum ^k _{i=2}d_e(q _i,q _{i-1})}{d _e (x _g , x _0 )}$$其中 \(x_O\) 是当前车辆的位置。

最后，我们还寻求最小化最大轨迹曲率的乘坐舒适性。由于b样条允许解析曲率计算，我们将最大曲率代价设置为$$J_k(\mathbf{q})=\max \frac{||\sigma ' \times \sigma ''||}{||\sigma '|| ^3}$$其中 \(\sigma\) 是 \(\mathbf{q}\) 的 B 样条表示。

最终，最后，采用基于[41]的数值非线性优化程序进行求解$$\mathbf{q}_{opt}=\arg \mathop{\min}\limits _{\mathbf{q}\in \mathcal{X}}[J _d(\mathbf{q}),J_l(\mathbf{q}),J_k(\mathbf{q})]W^T_q$$得到最优轨迹。其中 \(W_q\) 是一个权重向量，用于调整成本函数项的相对重要性。

请注意，在我们的农村测试环境中，用于测试的道路是没有标记的，通常是单宽的。因此，成本函数优先沿着道路中心行驶。为了在多车道的道路上使用，我们可以很容易地将该成本函数扩展为包含一个基于车道边界的成本项。

实验

• 车辆是2015年的丰田普锐斯V型自动驾驶改装车
• 使用Velodyne HDL-64S3激光雷达传感器进行感知
• 同时使用Microstrain 3DM-GX4惯性测量单元(IMU)
• 外部车轮编码器进行车载里程测量。
• 整个管道的PERCEPTION和PLANNING部分是在标准笔记本电脑上使用Intel-i7四核处理器进行的
• 使用一个单独的笔记本电脑(具有类似的规格)来运行低级控制和传感器驱动程序。
  • 这种分离确保了高级感知和规划线程中的延迟不会导致低级控制器中的延迟，低级控制器需要以更高的频率运行。这两台计算机通过机载以太网进行通信。

由于传感器能够以5Hz频率感知前方35米的道路，并且车辆达到了10m/s的最大速度，道路分割的频率足够快，以确保车辆在准备纳入新的传感器数据之前，沿着已知的道路样条行驶最多2米或<5%。

我们将MapLite系统集成到一个完全自主导航的管道中，能够操作车辆从任意起点到用户指定的目标位置。为了执行由变分规划器生成的运动计划，我们实现了一个纯追踪控制器[17]，它使我们能够选择一个d = 8m的前向距离，这个距离足够大，以确保乘坐着的舒适性，同时也足够小，以紧密地跟随参考路径。

我们使用动态速度控制器设置车速，使其符合以下约束条件:

1. 最大速度
2. 最大线性加速度
3. 最大线性减速度
4. 最大限度的向心加速度

速度控制器首先通过模拟纯追踪控制器向前移动固定距离来生成一个预测路径，然后解析求解在预测路径长度范围内的最大速度。

纯追踪和动态速度控制器的输出是指令转向角度和速度。为了利用鲁棒闭环控制实现这些指令，设计了一对PID控制器。这些PID控制器的每个调整，以获得快速响应速度和转向命令，同时最大限度地减少超调和稳态误差。

测试场地

这些道路是单车道的，大部分没有标记，在边界上没有路边或障碍物。道路被森林和植被包围。这些特征会随着季节的变化而变化，这使得绘制这一农村环境的高清晰度3D地图变得尤为困难。

Ground Truth

为了评估提出的方法，我们使用了一个实时运动学GPS惯性导航系统(型号:OXTS-RT3003)，该系统带有一个基站发射差分GPS修正。该基站提供地面真实位置和方向，精度为2厘米，射程为10公里。

请注意，RTK-GPS系统只用于获取地面真实情况，并在车辆开始移动前加载地图时提供初始位置。在导航过程中，车辆只能获得里程数测量数据，并完全使用MapLite系统进行漂移修正。图4-3为自主驱动的示例轨迹。蓝色的路径是由mapplite选择的，而绿色的路径是由里程数估计的。显然，如果没有mapplite的修正，里程数的漂移会很快导致车辆偏离路面。