自旋电子学笔记-张曙丰

说明

本课程是张曙丰在2012年左右的自旋电子学课程，可以查看网址
主要讲述了在金属磁性材料中的基本知识！
简单目录：
1-5集是磁学简单概念和相互作用。
6-10集是磁动力学。
11-18集是几个subject。
19-21集是具体应用。

：：1

顺磁性：

随着时间的演变，材料磁性始终保持无序。
金属导电的电子顺磁性称为泡利顺磁性。

泡利顺磁性推导

（来源：铁磁学上册P56）
在相空间中，每个体积为\(h^3\)的相格只能有两个电子。单位体积中电子数：
\(n=2\times \frac{4}{3}\pi P_F^3/h^3 = \frac{8\pi}{3h^3}(2mE_F)^{3/2} = N(E)dE\)
其中\(N(E)=\frac{4\pi}{h^3}(2m)^{3/2}E^{1/2}\)，为电子按能量的分布，称为态密度。在\(H=0,T=0K\)时\(N_+=N_-\)

当存在外磁场时时，磁场引起的能量变化为\(\mu H\)，因此只有费米面附近少量的电子才参与转移。
\(\delta N_+ = \frac{1}{2}N\mu_B H\)
\(\delta N_- = \frac{1}{2}N\mu_B H\)
所以相应的磁化强度应为：
\(M= (\delta N_+ - \delta N_-)\mu_B = N(E_F)\mu_B^2H\)
所以顺磁磁化率为\(\chi_顺^电子=\frac{12m\mu_B^2}{h^2}(\frac{\pi}{3}^{2/3}n^{1/3})\)

spin glass

主要体现在冻结上，依然是磁有序，但是不是所有的磁矩都有规律排列，微观看依旧是随机的，但是宏观有净磁矩。并且不随时间改变。有冻结温度\(T_f\)

超顺磁

随时间整体改变磁矩方向。

一般不考虑轨道角动量原因

对于轨道波函数的解：\(Y_{2,1}\)和\(Y_{2,-1}\)总是在一起的，只能在小的范围内break掉。

海森堡模型

\(\sum\limits_{i,j} S_i S_j\)
海森堡交换作用并不是磁偶极子相互作用。它的来源是电子的相互作用，库仑相互作用进一步来源于泡利不相容原理。
交换两个电子后，他们的波函数相反，这意味着，当轨道部分对称时，自旋部分必须反对称。当自旋部分对称时，轨道部分必须反对称。
由于单重态和三重态的存在会导致 overlap Coulomb integral
如果是相同的自旋，波函数如果想要在一起库仑相互作用就会增强。如果是相反的自旋，波函数要分开，库仑相互作用减弱。在固体里面原子靠得近，作用力很强！
假设哈密顿量
\(H = (E_1 - E_2)\frac{S^2}{2}+E_0 \propto -JS_iS_j\)
考虑J的大小，当晶格常数比较大的时候，电子的库仑排斥也会见效，J减小。当晶格常数比较小的时候，电子间库仑相互作用比较强，J比较大。
还有各向异性的模型，Ising model这个主要是平面内各向同性，z方向各向异性。或者z方向加强磁场，能量比J还要大。

平均场理论

$M(T) = gS\mu_BB_s(gM(T)/K_BT) $，

其中
\(B_s(x)\)是布里渊函数。

自旋波理论

$M(T) = M_0 - S\sum\limits_k n_k $
\(n_k = \frac{1}{e^{\varepsilon}-1}\)
\(\varepsilon = Ja^2k^2+g\mu_BH\)

：：2
在低温时使用自旋波理论，高温时使用平均场理论。
自旋波理论可以解释为什么有分数的\(\mu_B\).
铁磁矩
\(\mu = 2.2\mu_B\)
Co磁矩
\(\mu = 1.6\mu_B\)
Ni磁矩
\(\mu = 0.6\mu_B\)

自由电子模型

\(E_k \propto n_{\downarrow}^{\frac{5}{3}}+n_{\uparrow}^{\frac{5}{3}}\)
\(E_{ex} \propto U_{n_{\downarrow \uparrow}}\)
这里有点疑问？为什么动能正比于\(n_{\downarrow}^{\frac{5}{3}}+n_{\uparrow}^{\frac{5}{3}}\)

stoner model of ferromagnetism

\[E_{total} = E_k +E_{ex} = A(n_{\uparrow}^{\frac{5}{3}}+(n-n_{\uparrow}^{\frac{5}{3}})) +U_{n_{\uparrow (n-n_{\uparrow})}} \]

铁磁性条件：一阶偏导为0，二阶偏导大于0.得到
\(N(\varepsilon_F)U>1\)

N为费米面态密度，U为库仑积分。

homework1

利用stoner model 计算二维的临界条件。
二维铁磁性定理：
Mermin-Wagner定理，利用海森堡模型在二维材料中不存在长程磁有序。 这里主要是考虑各向同性，如果是各向异性在二位材料可以产生磁性。

参考文献：
Mermin, N. D., & Wagner, H. (1966). Absence of ferromagnetism or antiferromagnetism in one-or two-dimensional isotropic Heisenberg models. Physical Review Letters, 17(22), 1133.

：：3

磁相互作用

自旋电子学主要研究室温下的现象，这个时候单纯的量子效应较弱，这个时候主要考虑经典（半经典）的效应。

交换能

A:交换常数。
\(H = -J\sum\limits_{i,j}S_i S_j = -J\int dx{M(x)\cdot (M(x+1)+M(x-a))}\)

假设M(x)随x是缓慢变化的。 假设模不变。
\(M(x+a) = M(x) + a\frac{\partial M(x)}{\partial x} + \frac{1}{2} a^2 \frac{\partial M(x)^2}{\partial^2x}\)
\(M(x-a) = M(x) - a\frac{\partial M(x)}{\partial x} + \frac{1}{2} a^2 \frac{\partial M(x)^2}{\partial^2x}\)
\(M(x+a) + M(x-a) = Const + a^2 \frac{\partial M(x)^2}{\partial^2x}\)

\(E = -\frac{J a^2}{M^2} \int dx M(x) \cdot \frac{\partial M(x)^2}{\partial^2x}\)

\(E = - \int dx M(x) \cdot H_{eff}\)

\(H_{eff} = \frac{Ja^2}{M^2} \frac{\partial M(x)^2}{\partial^2x} = A \frac{\partial M(x)^2}{\partial^2 x}\)

$H_{eff} = A \nabla^2 \mathop{M}\limits^{\to} $

\(E = \int \frac{A}{2 \cdot M^2} \nabla^2 M\)

这里使用到了分步积分。 \(\frac{\partial}{\partial x} M \cdot \frac{\partial M}{\partial x} = (\frac{\partial M}{\partial x})^2 + M \cdot \frac{\partial M^2}{\partial^2 x} = \frac{1}{2} \frac{\partial M^2}{\partial x} = 0\)

形状各向异性 退磁能

\(E_d = - H \cdot M\)

\(H_d = -N_d \cdot M\)

薄膜材料：

面内形状各向异性：\(\nabla \cdot H_d = -4\pi \nabla \cdot M\)
\(H_d^z = - 4 \pi M_z = -4\pi M_s cos(\theta)\)
\(E_d = 2 \pi M_s^2 cos(\theta)^2\)

体效应

退磁能\(E_d = M_s^2ab^2\)
畴壁能\(E_w = \sigma_w ab\)
临界大小 \(b = \sigma /M^2\)

磁滞回线

矫顽力较小：软磁
矫顽力（coercivity）大：硬磁。

stoner - Wohlfarth model

\(E = -HMcos(\theta) - K sin(\varphi - \theta)^2\)
一阶偏导为0，二阶偏导大于0。
\(\phi\)为易轴和磁场H的方向。\(\theta\)为M和H的方向夹角。
H的方向为z轴方向。
jump:一阶导数为0，二阶导数为0 并且\(M = M_s cos\theta\)
\(\frac{\partial E}{\partial \theta} = HMsin\theta - K sin2(\phi - \theta) = 0\)
\(\frac{\partial^2 E}{\partial \theta^2} = HMcos\theta +2K cos2(\phi - \theta) = 0\)
由于\(M_s\)是常数，所以我们可以查看\(cos\theta\)与H的关系。例如当\(\phi = 0\)时，从一阶导为0，二阶导大于0可以得到\(\theta = 0 或者 \pi\),这样，我们可以得到最基础的磁滞回线版本。它的跳跃发生在二阶导为0处因此可以得到矫顽力的大小。
注意这里不要随便约去\(sin\theta,cos\theta\)，因为这些变量可能为0.

homework2

计算磁滞回线\(\varphi = \frac{\pi}{4}, \frac{\pi}{3}\)

：：4,5
Asteriod :第一代MRAM
\(E = -M_sH_acos\theta -M_sH_bsin\theta +Ksin^2\theta\)
临界条件：一阶偏导，二阶偏导为0，解得：
\(H_a = -\frac{2K}{M_s}cos^2\theta\)
\(H_b = \frac{2K}{M_s}sin^2\theta\)
于是有：
\(H_a^2+H_b^2=(\frac{2K}{M_s})^2\)，称为磁翻转条件。

RKKY

中间通过费米海为媒介进行相互作用的传播。

此时的哈密顿量为：
$H_{int} = -JS_1$

homework4

在磁性材料中掺杂稀磁半导体，在二维情况下RKKY更强！

::6

畴壁能

畴壁能是交换能和各向异性能交换的结果。总能量：
$E = E_{ex} + E_{an} = A\frac{\pi^2}{2L2}L + \frac{K}{2}L $
取总能最小
\(E_{w} = \pi \sqrt{AK}\)
\(L_w = \pi \sqrt{\frac{A}{K}}\)

neel壁与bloch壁

对于薄膜而言，在畴壁中间，neel壁中磁化方向是在膜内。bloch垂直于薄膜。
薄膜越薄neel壁能量越低，两种畴壁的交叉点大致为30-50nm。

交换偏置

对于反铁磁加磁场，这个时候相同方向能量降低，相反方向能量升高，总能量不变，所以对反铁磁没有影响！
对于铁磁很容易就会转过去。

磁动力学

LLG方程
$\frac{dM}{dt} = -\gamma H_{eff}\times M + \frac{\alpha}{M_s} M \times \frac{dM}{dt} $
\(\frac{dM}{dt} = -\gamma H_{eff} \times M - \frac{\alpha \gamma}{M_s} M \times (M \times H_{eff})\)
对于进动项：
\(\frac{dM}{dt} = -\gamma H_{eff} \times M\)
对于阻尼项：
\(\frac{dE}{dt} = H_{eff} \times \frac{dM}{dt} = - \frac{\gamma \alpha}{1+\alpha^2} |M\times H_{eff}|^2\)
阻尼项一直小于0，所以逐渐减慢。

::7

LLG方程的性质

第一，M的模不变。证明：可以在LLG方程两边同时\(\times M\)可以得到0，所以M的模不变。
第二，平衡位置一定是M与H方向一致。
第三，频率在GHz。

共振频率与共振宽度

通过共振频率和共振宽度可以计算出LLG方程中的常数系数。
施加一个带有微小扰动的外加磁场
\(H = H_0 e_z+(h_xe_x+h_ye_y)e^{iwt}\)
此时磁化矢量M为：
\(M = M_se_z+(\delta m_x e_x + \delta m_y e_y)e^{iwt}\)
\(\delta m_z = \delta m_x^2 + \delta m_y^2 = 0\)
\(\delta m_y = \frac{ah_x+bh_y}{w^2-w_r^2+i\Gamma}\)
\(\delta m_x = \frac{-bh_x+ah_y}{w^2-w_r^2+i\Gamma}\)
其中\(a = -\gamma M_s (1+\alpha)^{-1}(\gamma H_0 + i\alpha w),b=-\gamma M_s (1+\alpha)^{-1}( i\alpha w)\)
所以共振频率为：
\(w_r = \frac{\gamma H_0}{\sqrt{1+\alpha^2}}\)
共振宽度为：
\(\Gamma = 2\alpha ww_r\)

自旋输运

Drude model

\(j=\sigma E,\sigma = \frac{ne^2\tau}{m}\)

Hall Effect

\(F = ev\times B,j=nev,E=F/e\)
所以有：
\(E = \frac{1}{ne} j\times B\) 可以测量霍尔系数来测量n
但是在磁性材料中，例如Fe,Co.可以得到\(E_h. = \rho_H j\times M\)
其中$\rho_H >> \frac{1}{ne} $ 这里是“反常霍尔效应”？，原来一直用散射理论解释，现在也开始用berry phase来解释。
这里根本原因是由于SOC引起的。

spin hall current

主要是非磁性材料，Ta,Pt,Au,自旋霍尔角在0.1左右。在半导体材料可以使用光学方法测量，但是在金属材料无法测到。
电流为：\(j_{\sigma} = cE + c_h \sigma \times E,tan(\theta_H) = \frac{c_h}{c}\)

::8

incerse spin hall

自旋流产生逆电荷流。非磁性材料。
\(j_e = \frac{c_h}{c}\sigma \times j_e\)
为什么SOC能产生垂直方向的电流？
\(H = \frac{p^2}{m} + \zeta_{soc} (r\times p)\cdot \sigma\)
\(<v> = <\frac{1}{i\hbar}[r,H]> = \frac{<p>}{m} + <\zeta_{soc} (\sigma \times r)>\)

Anistropic Magnetoresistance(AMR) 各向异性磁阻

\(R(\theta) = R_{\perp}+(R_{\parallel}- R_{\perp})cos\theta\)
一般有：
\(\frac{R_{\parallel}-R_{\perp}}{R_{\perp}} \le 2\%\)
AMR的来源可以使用唯象理论解释。
当电流方向和磁场方向相同时，这个时候电子运动轨道于电流运动方向垂直，散射面积更大，所以电阻较大。
当电流方向和磁场方向垂直时，此时电子运行轨道平行于电流运动方向，散射面积小，所以电阻小。

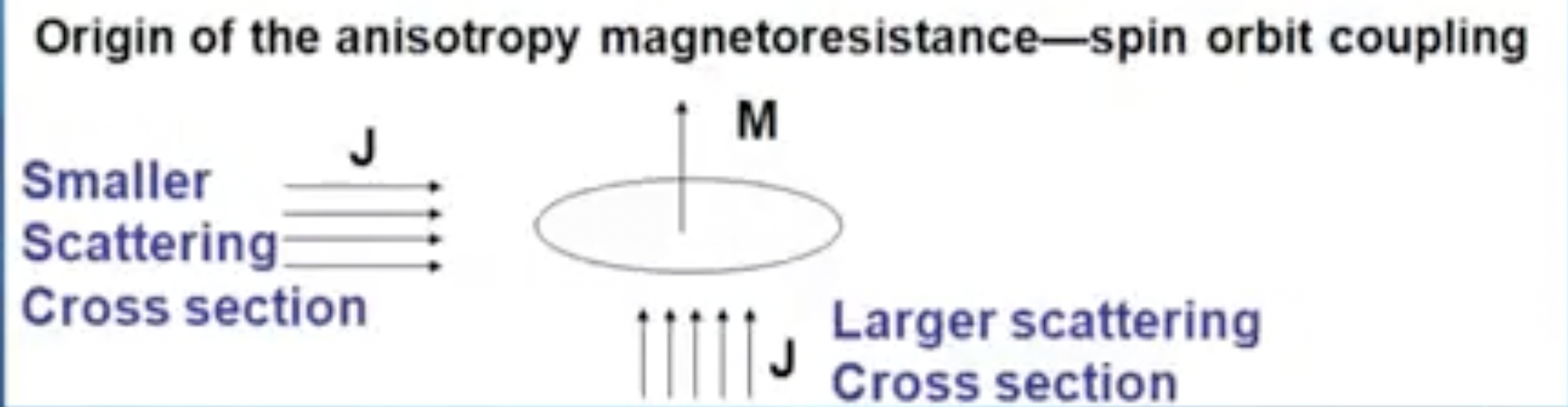
planer Hall Effect 平面霍尔效应

实际上平面霍尔效应并不是真正的霍尔效应而是AMR效应。
通过AMR效应进行计算：
\(j_{\parallel} = j_{x}cos\theta + j_{y} sin\theta = \sigma_{\parallel}(E_y cos\theta +E_x sin\theta)\)
\(j_{\perp} = j_{x}sin\theta + j_{y} cos\theta = \sigma_{\perp}(-E_y sin\theta +E_x cos\theta)\)
so, 在实际测量中，\(j_y = 0\)
$E_y = (\rho_{\parallel} - \rho_{\perp})j_x sin\theta cos\theta $
我们可以看到当\(\theta = \frac{\pi}{4}\)时，测量信号取最大值，当\(\theta = 0 或者 \frac{\pi}{2}\)时取0.所以这个比值会很大，但是这并不是hall effect引起的而是AMR。

::9

玻尔兹曼统计

描述这个粒子使用了量子方法。这里主要是说明了随着薄膜次材料半径的增加，电阻率不断下降，另外薄膜材料的电阻率也和材料边界的电子反射率p有关，当p=1时，电阻率不随d变化，p越小，说明散射越多，电阻率越高。

::10

GMR 巨磁阻效应

平行： 电子散射较小，电阻较小。
反平行： 电子散射更强，电阻较大。

CIP：电流平行于薄膜。
CPP：电流垂直于薄膜。很明显电流垂直于薄膜时，GMR效应更加明显。

自旋积累

对于经典情况下两个金属有：
\(j_1 = \sigma_1 E_1 , j_2 = \sigma_2 E_2\)
同时有：
\(Q = (E_1 - E_2 ) \epsilon_0\)
因此在两个金属的界面上一定要电荷积累。 同样对于自旋流来说从铁磁金属到非磁性金属有：
\(j_{\uparrow}^F = \sigma_{\uparrow}^F E_{\uparrow} = - \sigma_{\uparrow} \frac{\partial V_{\uparrow}}{\partial x}\)
\(j_{\downarrow}^F = \sigma_{\downarrow}^F E_{\downarrow} = - \sigma_{\downarrow} \frac{\partial V_{\downarrow}}{\partial x}\)
自旋磁矩：\(m = \mu_B (n_{\uparrow} - n_{\downarrow}) = \mu_B N(\epsilon_F) e(V_{\uparrow} - V_{\downarrow})\)
自旋连续性方程：\(\frac{\partial m}{\partial t} - \frac{\mu_B}{e}\frac{\partial}{\partial x} (j_{\uparrow} - j_{\downarrow}) = - \frac{m}{\tau_{if}}\)
自旋扩散方程，此时\(\frac{\partial m}{\partial x} = 0\),所以\(\frac{d^2m}{dx^2} = \frac{m}{\lambda^2}\)
其中扩散长度 \(\lambda = \sqrt{\sigma \tau_{if}/e^2N(\epsilon)} = \sqrt{3v_{F}^2 \tau \tau_{if}}\)
下面对方程进行求解，
$x<0, V_{\uparrow} - V_{\downarrow} = Aexp(x/\lambda ) $
$x>0, V_{\uparrow} - V_{\downarrow} = Aexp(-x/\lambda ) $
当x=0时，电压相同有\(A=B\),于是有：
\(j_{\uparrow}^F - j_{\downarrow}^F = \frac{\sigma_{\uparrow} - \sigma_{\downarrow}}{\sigma_{\uparrow} + \sigma_{\downarrow}}\)
\(j_{\uparrow}^F - j_{\downarrow}^F = -\frac{\sigma^N B}{2\lambda_N}\)
对于有自旋积累的双材料模型的电阻(欧姆电阻和自旋积累引起的电阻)：
$R = V(L_2) - V(-L_1) = \frac{e j_e L_2 }{2 \sigma^N} + \frac{e j_e L_1}{2 \sigma^F} + \delta R $
其中\(\delta R = \frac{D}{2 \sigma^N} - \frac{D}{2\sigma^F} = \frac{P^2 j_e}{\frac{\sigma^N}{\lambda_N} + \frac{(1-P^2)\sigma^N}{\lambda_F}}\) 为自旋积累引起的电阻。
对于半金属：
\(P = 1,\delta R = \rho^N \lambda_N\)
所以半金属材料的电阻\(\delta R\)还是很大的
对于半导体材料电导率两者并不匹配，因此会导致效应十分微弱。 主要是\(\sigma^N << \sigma^F\).
\(\frac{j_{\uparrow}^{N} - j_{\downarrow}}{j_{\uparrow}^{N} + j_{\downarrow}} = \frac{P^2}{1-P^2}\frac{\lambda_F}{\lambda_N}\frac{\sigma^N}{\sigma^F}\)

Johnson - Silsbee experiment （1985）

在一边有自旋流，会扩散到另一极产生电压。并且两极的磁矩取向影响电压正负。

home work11

计算\(R_{AP} - R_{P}\),两个金属分别使用同向磁矩和反向磁矩。

：： 11

磁隧道结

隧穿电阻
电流：\(j(V) = e \int{d^3k P(E_k,V_{\perp}) (f_k(E_k) - f_k(E_k + eV))}\)
电导：\(G = j/V = e^2 \int{d^3 P(E_k,V_{\perp}) \delta (E_F-E_k)}\) 态密度？
P(E_k,V_{\perp})是隧穿概率。
对于中间势垒是常数：
解： \(U_b = Ae^{kz}+ B e^{-kz},k = \sqrt{\frac{2m(U-E)}{\hbar^2}}\)
当中间势垒为线性函数时 \(Az + B\)时：
方程为艾里方程：\(\frac{\hbar^2 \psi^{''}}{2m} + (Az + B) \psi = \epsilon \psi\)
解的形式为： \(\psi = C(z)e^{kz}\)

simmons tunnel model

\(G = a + bV^2 + ...\)
\(G = a + bT^2 + ...\)
\(R \propto exp(1.025t_b \sqrt{V_B})\)

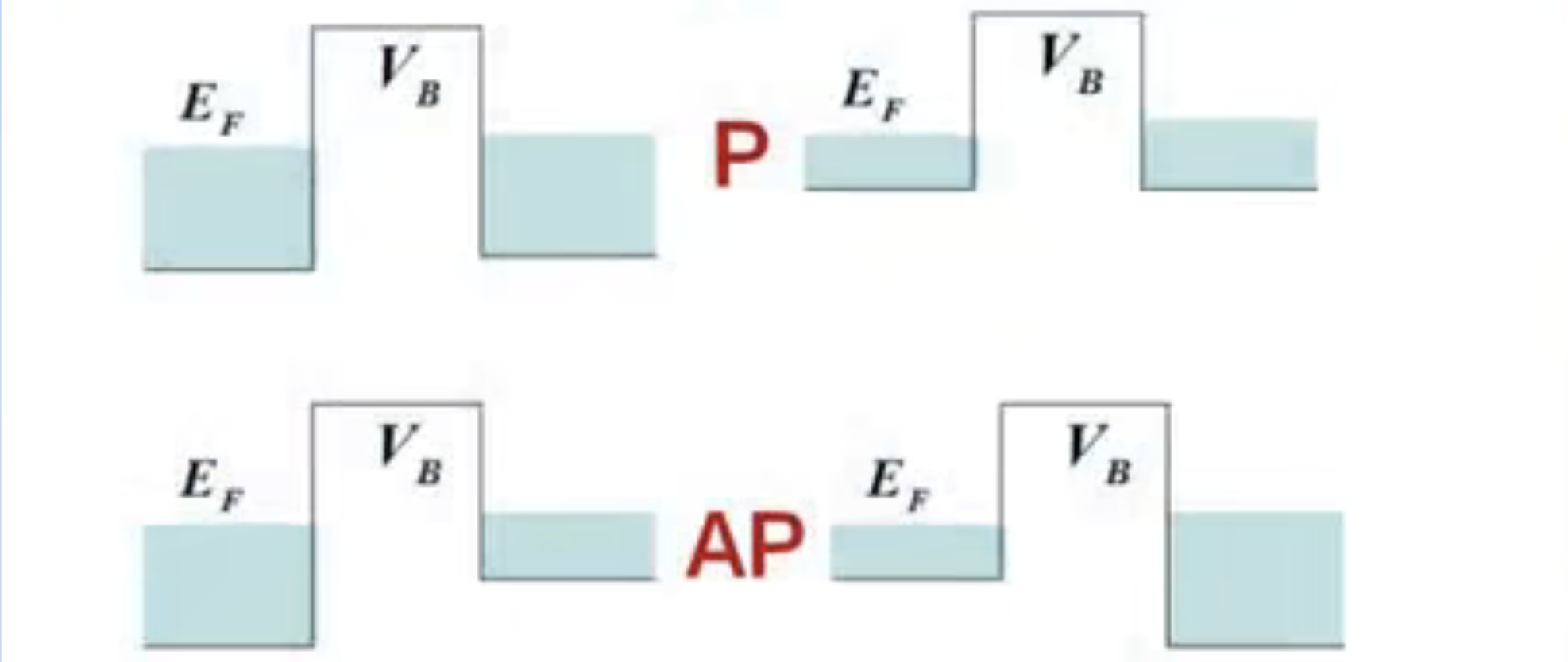
在上面的情况中，隧穿也要发生变化：
$P(k_L,K_R) = \frac{16 k_L k_R K_0^2}{(K_L2 + K_0^2)(K_R2 + K_0^2)} exp(-2 k_0 t) $
\(k_L = \sqrt{\frac{2m(\epsilon_F - V_L)}{\hbar^2}}\)
\(k_R = \sqrt{\frac{2m( V_R - \epsilon_F)}{\hbar^2}}\)

:: 12
设费米面处能量为0，则有：\(\epsilon_k = \frac{\hbar^2 k_z^2}{2m} - u\),u为从底到费米面的能量绝对值。
在绝缘层的波函数为\(\psi = Ae^{kz}+ Be^{-kz},k=\sqrt{\frac{2m}{\hbar^2}(V - \epsilon_k)}\)
当\(k_0 >> k_L,K_R\)时，\(P_{\uparrow \uparrow} = (k_{\uparrow \uparrow})^2 + (k_{\downarrow \downarrow})^2\)
\(P_{\uparrow \downarrow} = 2k_{\uparrow \downarrow}k_{\downarrow \uparrow}\)
\(\frac{P_{\uparrow \uparrow} - P_{\uparrow \downarrow}}{P_{\uparrow \uparrow} + P_{\uparrow \downarrow}} = (\frac{k_{\uparrow} - k_{\downarrow}}{k_{\uparrow} - k_{\downarrow}})^2\)
根据$d^3k = \rho \epsilon,k^2dk ~ \rho \epsilon , \epsilon d\sqrt{\epsilon} = \rho \epsilon $
所以\(p~ \sqrt{\epsilon} ~ k_F\)
所以：\(\frac{P_{\uparrow \uparrow} - P_{\uparrow \downarrow}}{P_{\uparrow \uparrow} + P_{\uparrow \downarrow}} = (\frac{k_{\uparrow} - k_{\downarrow}}{k_{\uparrow} - k_{\downarrow}})^2 = (\frac{P_{\uparrow} - P_{\downarrow}}{P_{\uparrow} + P_{\downarrow}})^2 = P_{极化率}^2\)

Julliere model of TMR

求自旋极化因子P。
隧穿电导：$G \propto N_L(\epsilon_F) N_R(\epsilon_F) $
平行电导：\(G_P \propto N_L^{\uparrow}N_R^{\uparrow} + N_L^{\downarrow}N_R^{\downarrow}\)
反平行电导：\(G_{AP} \propto N_L^{\uparrow}N_R^{\downarrow} + N_L^{\downarrow}N_R^{\uparrow}\)
\(TMR = \frac{G_P - G_{AP}}{ G_{AP}} = \frac{P_LP_R}{1-P_LP_R}\)
所以自旋圾化因子：$P_{L,R} = \frac{ N_{L,R}^{\uparrow} - N_{L,R}^{\downarrow} }{N_{L,R}^{\uparrow} + N_{L,R}^{\downarrow}} $

home work 12&13

证明穿透系数
在Co和半金属材料中使用Julliere model

STT

磁矩从一端进入，从一端出去，但是方向发生了改变，那么就必须有净的磁矩积累。就会导致里面的磁矩旋转。
使用连续性方程：\(\frac{\partial \rho}{\partial t} + \nabla \cdot J = 0\)
可得： \(- \frac{dM}{dt} = -(J_{in} - J_{out})_{\perp} = a_{J} M \times (M \times M_{p})\)
其中： \(a_J = \frac{\mu_B P J^e}{e}\)

：： 13
进动项加上阻尼项加上自旋力矩项的的LLG方程：
\(\frac{dm}{dt} = - \gamma m \times H_{eff} + \alpha m \times \frac{dm}{dt} + a_{J}m \times (m \times m_P)\)
这也是自旋阀理论方程。
进动项使得磁矩m不断旋转，阻尼项使得最终m趋向磁场h方向，当\(a_J < 0,即电流J<0\)时，力矩方向与阻尼项方向相反。

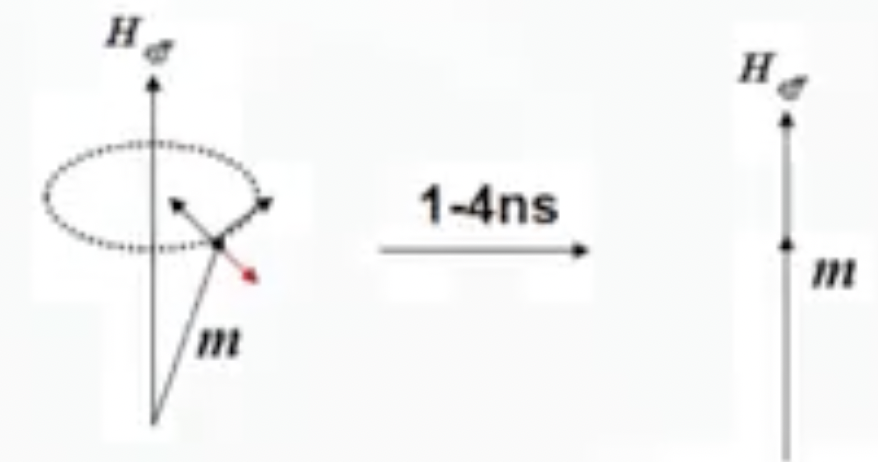
这里需要注意下，在赛曼能中有\(E = -H_{eff}M\)但是在一般的情况下是\(H_{eff}= - \frac{\partial E}{\partial m}\),所以就有：$\frac{dE}{dt} = - H_{eff} \frac{dm}{dt} $
能量变化速率：\(\frac{dE}{dt} = - \alpha \beta |H_{eff}\times M|^2 + a_{J}(\alpha M_P - m \times M_P)\cdot (m \times M_P)\)
前一项是阻尼项后一项是自旋力矩产生的泵浦项。pumping 这一项是十分复杂的，如果为负那么可能造成磁矩的翻转。如果为0可以产生交流信号，并且scale是很小的，频率也很大。

非线性 Melnikov function

\(\delta E = - F(E),F(E) = 0,F(E)^{'} > 0,stable state\)
DC信号进去会产生AC信号！

spin pumping

提出一个东西记得问它的反效应。spin pumping 就是STT的反效应。
电流--> pumping
current --> torque --> magnetion precession
Feremagnetic --> precession --> spin current:\(M = M_0 + m coswt,j_s = AM\times \frac{dM}{dt}\)

::14

绝热与非绝热力矩

\(j_s(x+dx) = P j_e M(x+dx)\)
\(j_s(x) = P j_e M(x)\)
\(\Delta j_s = P j_e [M(x+dx) - M(x)]\)
体积内总的磁矩:\(Mdx\)
力矩： \(\frac{d(Mdx)}{dt} = P j_e \frac{dM}{dx}\)
磁矩m是守恒量所以有：$ \frac{d(Mdx)}{dt} = \frac{\mu_B j_s}{e}\frac{dm}{dx} = \frac{\mu_B j_s}{e} m \times (m \times \frac{dm}{dt})$
导带电子运动方程：\(\frac{\partial m}{\partial t} + \nabla \cdot J = - \frac{1}{\tau_{ex} M_s} m \times M - \frac{\delta m }{\tau_{sf}}\)
magnetization 磁化方程：
\(\frac{\partial M}{\partial t} = - \gamma M \times H_{eff} + \alpha M \times \frac{\partial M}{\partial t} b_J M \times (M \times \frac{\partial M}{\partial x}) + c_J M \times \frac{\partial M}{\partial x}\)
其中：\(\frac{c_J}{b_J} \approx 0.01\)，虽然比较小，但是在domain wall 作用很大，因为一般其和第二项进行比较。

总结

spin valves:
\(\frac{dm}{dt} = - \gamma m \times H_{eff} + \alpha m \times \frac{dm}{dt} + a_{J}m \times (m \times m_P)\)

三项分别是：进动项，阻尼项，力矩项
Tunnel junctions:
\(\frac{\partial m}{\partial t} = - \gamma m \times H_{eff} + \alpha m \times \frac{\partial m}{\partial t} a_J m \times (m \times m_P) + b_J m \times m_P\)
最后一项是有效场项
Domain wall:
\(\frac{\partial m}{\partial t} = - \gamma m \times H_{eff} + \alpha m \times \frac{\partial m}{\partial t} b_J m \times (m \times \frac{\partial m}{\partial x} + \frac{\beta b_J}{M_s} m \times \frac{\partial m}{\partial x})\)
最后两项分别是绝热项和非绝热项。

：：15
要想写成势能形式必须是保守力。

home work

为什么\(m\times m_P\)不能写成一个函数的梯度，即不是保守力。与积分路径有关？
临界电流的计算。
\(M = M_s + \delta e^{iwt}\) ,\(\delta\)是一个小量偏转，带入LLG方程。
这里有一个关键的条件：w的虚部为0，当虚部小于0时不稳定。为什么呢？因为在e指数上iwt如果w虚部是小于0，那么整体就是大于0，最终随时间增大一定是发散的。
\(a_J = \alpha (2\pi M_s + H_k - H)\)
不稳定的判断条件，a一般比较大。\(H_k\)为各向异性场。
不稳定之后存在两种解，一种是直接反平行，磁矩翻转。另一种做进动。
从LLG方程可以得到：
\(\frac{dE}{dt} \propto - \alpha |M \times H_{eff}|^2 +a_J (\alpha M_P- M \times M_P)\cdot (M \times M_P)\)
第一项一定是正的，第二项可正可负，甚至随之时间改变正负。当\(M_P//H_{eff}\)时，有：
\(\frac{dE}{dt} \propto (-\alpha + \frac{a_J}{H_{eff}})|M\times H_{eff}|^2\)
单独的STT已经被研究了很多，但是还需要和其他效应结合。
这里后面还涉及到了一些弛豫时间时间和自旋波相关。

：：16

spin-dependent Ohm's Law

电流：\(j_i^e = \sigma^{\uparrow}E^{\uparrow} + \sigma^{\downarrow}E^{\downarrow}\)
自旋流：\(j_i^s = \frac{g\mu_B}{e} (\sigma^{\uparrow}E^{\uparrow} - \sigma^{\downarrow}E^{\downarrow})\)
整理后：
电流：\(j_i^e = \frac{\hbar P \sigma_0}{4 e^2} (\partial_t M \times \partial_i M)\cdot M\)
自旋流：\(j_i^s = \frac{g\mu_B\hbar \sigma_0}{4e^2} (\partial_tM \times \partial_i M)\)
考虑一个一维螺旋磁畴结构：\(\theta(x,t) = \theta(x-vt),\phi(x,t) = \phi_0 + wt\)
电压\(V = \int{\rho j_i^e dx} = P \frac{\hbar w}{2e}\)
在畴壁转动过程中能量随时间的变化为；$\frac{dE}{dt} = - \gamma \alpha_0 |M \times H_{eff}|^2 - \gamma \eta \sum |\partial_i M \cdot H_{eff}|^2 $
第一项是正常的阻尼项，第二项是由于焦耳热产生的，因为：\(Q = G^{\uparrow} E^{\uparrow 2} + G^{\downarrow} E^{\downarrow 2} = \gamma \eta \sum |\partial_iM \times H_{eff}|^2\)
可以理解为，电子运动产生电流，因为有焦耳热。

SOC

对于单个原子的自旋轨道耦合哈密顿量:\(H_{so}^{at} = \frac{e\hbar}{2m^2e^2} (\nabla V^t \times P)\cdot \sigma\)
对于固体中自旋轨道耦合哈密顿量为：\(H_{so}^{at} = \zeta_{so} (\nabla V^{en} \times P)\cdot \sigma\)
在半导体中：\(\zeta_{so} \propto \frac{1}{E_g^2} - \frac{1}{(E_g^2 + \delta_{so})^2} = 1000 \times \frac{e\hbar}{2m^2e^2}\)
这里主要是因为势能在固体里面取了平均，实际的变化很可能是剧烈的。所以差了1000倍。
在铁磁表面的哈密顿量：\(H = \frac{P^2}{2m} + V + \alpha (\nabla V \times P)\cdot \sigma - J \sum M_i M_j - J_{ex}M_i \sigma\)
考虑最简单的情况，在界面处：\(H = \frac{P^2}{2m} + \alpha_{Ra}(z\times P)\cdot \sigma - J_{ex} M\cdot \sigma\)
前两项就是半导体中的Rashba效应的哈密顿量。 之后是交换能。

：：17
这一集和16集重复了。

:: 18
证明在金属-绝缘体表面的\(H = H_{Ra}\)
$H_R = \alpha_{so}(\nabla V \times P)\cdot \sigma >> H_{Pauli} = \frac{\hbar \mu_B}{2mc^2}(\nabla V \times P)\cdot \sigma $
表面势为：$\nabla V = (W + E - \chi) \delta (z) $
所以$H_R = \alpha_{R} (z \times P)\cdot \sigma , 其中 \alpha_R = \alpha_{so}(W + E - \chi) \delta (z) $
对于交换能，自旋向上的体系中，在k空间所有自旋都是朝上；自旋向下的体系中，在k空间所有自旋都是朝下；
对于Rashba效应，自旋向上的体系中，在k空间所有自旋都是顺时针，也就是自旋与k矢量（也就是M）垂直；自旋向下的体系中，在k空间所有自旋都是逆时针；

Miron NM 2010 2011

:: 19
Endo APL 2010

heat assisted writing

\(\Delta E = K_a V\)
\(\tau = \tau_0 e^{\frac{\Delta E}{kT}}\)
一般存储设备的年限至少要十年，那\(\frac{\Delta E}{kT}\)至少要50，所以V不能太小，但是随着存储密度的提高，这个体积V不断减少，这就有了一定限制。

：：20
所以材料的各向异性就得非常大，增大\(K_a\).例如材料Pt，Co。
在低温下势LLG，在高温下张曙丰老师发展了新的方程，加入了一项与弛豫时间有关。 当时还缺少实验的证实。

：：21

hard disk drive

FePt(L) 有10特斯拉。 各向异性很强。
虽然各向异性很强，但是这给写入又带来了困难。与19集有点相似。