W
e
l
c
o
m
e
: )

[考试记录] 2024.8.10 csp-s 模拟赛18

80 + 20 + 0 + 70 = 170 第三题应该有 10 分暴力的，但我没打。

T1 星际旅行

题面翻译

总共有n个节点，m条路径，要求其中m-2条路径走两遍，剩下2条路径仅走一遍，问不同的路径总数有多少，如果仅走一遍的两条边不同则将这两条路径视为不同。

样例 #1

样例输入 #1
5 4
1 2
1 3
1 4
1 5
样例输出 #1
6

样例 #2

样例输入 #2
5 3
1 2
2 3
4 5
样例输出 #2
0

解析

结论题 🤣

考场上没放输出 \(0\) 的那个样例，于是显然想不到非联通的那种方案。是我太\(菜\)了。

多手玩几个样例(1h)可以发现：

  • 对于没有自环的情况，假设将 \(rt\) 作为该条航线的出发点，那么手玩一下即可发现，能产生的合法航线数即为 \(rt\) 的儿子的儿子数量。emmm……有点绕。看图。

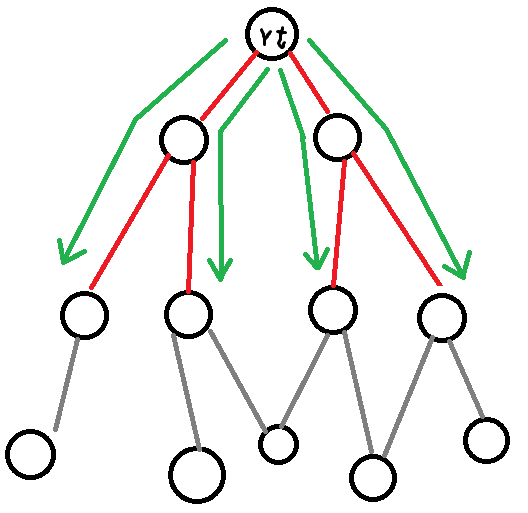
标红的线即为可能出现的只走一次的边，标绿色的线就是可能的走法。也就是每次从 \(rt\) 出发最终回到某个儿子的儿子上，这个儿子的儿子与 \(rt\) 连的边即为只走一次的边。那么 \(rt\) 对答案的贡献就是：

\[\sum_{v\in son[u]}size[v]-1 \]

其中，\(size\) 表示这个点与多少个点直接相连，因为不能算父亲，所以减一。总贡献即为：

\[{\large \sum_{u=1}^{n}}\sum_{v\in son[u]}size[v]-1 \]

  • 对于存在自环的情况，考虑两种情况：自环配自环、自环配普通边。
    • 自环配自环：方案数即为从所有自环里随机取出两条的组合：\({\large\binom{cir}{2}}\)。\(cir\) 为自环数。
    • 自环配普通边：方案数即为从所有自环里随机选一条和从普通边里随机选取一条。运用乘法原理：\(cir\times(m-cir)\)。

算完了？你猜为什么样例有个 \(0\)？如果存在某条边与其他所有的边都不联通，那么就无法走完 \(m\) 条边。所以要判边是否联通。运用并查集即可。

code 
#include<bits/stdc++.h>
using namespace std;
#define int long long
constexpr int N = 1e5 + 5;
int n, m, cir, ans1, ans2, f[N], x[N];
vector<int> G[N];
inline int find(int k){
	if(!f[k]) return k;
	return f[k] = find(f[k]); 
}
signed main(){
//	freopen("t1.in", "r", stdin);
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>m;
	for(int i=1, y; i<=m; ++i){
		cin>>x[i]>>y;
		int fa = find(x[i]), fb = find(y); 
		if(fa != fb) f[fb] = fa;
		if(x[i] == y){ ++cir; continue; }
		G[x[i]].push_back(y), G[y].push_back(x[i]);
	} int bg = find(x[1]);
	for(int i=2; i<=m; ++i) if(find(x[i]) != bg) return cout<<0, 0;
	if(cir) ans2 = cir * (cir-1) / 2 + cir * (m - cir);
	for(int i=1; i<=n; ++i) for(int v : G[i]) ans1 += G[v].size() - 1;
	ans1 >>= 1;	return cout<<ans1 + ans2, 0;
}

T2 砍树

题面

林先森买了 \(n\) 棵树苗，种在一条直线上，用来装点他的花园。初始时所有树苗的高度是 \(0\)，每过 \(1\) 天每棵树苗都会长高 \(1\) 米。对每棵树苗，林先森希望它 的最终高度为 \(a_i\)，因此他会定时检查树苗的情况，并及时砍掉过高的树苗。具 体来说，从种下所有树苗开始，每d天（即：第 \(d\) 天、第 \(2d\) 天，. . . ，以此类推） 林先森会检查一遍所有的树苗，如果有树苗的高度不低于他希望的高度，林先 森会把高出的部分（可以为 \(0\)）砍掉，之后这棵树苗便不再长高。由于砍树是一 件辛苦的工作，林先森希望砍掉的树苗的总长度不超过k米。在这个前提下， 为了偷懒，林先森想要知道最大可能的 \(d\) 值。

sample

3 4
1 3 5

3

解析

熊出没题

考场上脑子宕机拉了一泡二分答案，样例过了就没再管，喜提 \(20\) 分。下考后拿脚指头想都觉得二分没单调性。👀

考虑这么个事情。我们要找的 \(d\) 都满足这么个狮子：

\[\sum_{i=1}^{n}(\left \lceil \frac{a_i}{d} \right \rceil *d-a_i)\le k \]

移项得：

\[\sum_{i=1}^{n}\left \lceil \frac{a_i}{d} \right \rceil *d\le k+\sum_{i=1}^{n}a_i \]

这就清楚了。可以发现，我们可以枚举 \(\left \lceil \frac{a_i}{d} \right \rceil\) 和 \(d\) 的所有可能取值，暴力枚举判断即可。假设现在枚举到了一个可能的 \(d'\) 值。那么现在的 \(d\) 的取值范围就可以表示为：

\[d\le \frac{k+\sum_{i=1}^{n}a_i}{\sum_{i=1}^{n}\left \lceil \frac{a_i}{d'} \right \rceil} \]

如果 \(d'\) 在这个范围内，那么这个范围就是合法的。用这个范围的最大值更新答案即可。

code 
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n, k, a[101], ans;
vector<int> vec;
signed main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>k;
	for(int i=1; i<=n; ++i){
		cin>>a[i]; k += a[i];
		for(int j=1; j*j<=a[i]; ++j){
			vec.push_back(j);
			vec.push_back((a[i] + j - 1) / j);
		}
	}
	sort(vec.begin(), vec.end());
	vec.erase(unique(vec.begin(), vec.end()), vec.end());
	for(int it : vec){
		int sum = 0, d;
		for(int i=1; i<=n; ++i){
			sum += (a[i] + it - 1) / it;
		} d = k / sum;
		if(d >= it) ans = max(ans, d);
	} return cout<<ans, 0;
}

对于以后类似这种题的情况。提供两种解决思路：

  1. 枚举样例 + 手玩。找到规律。
  2. 列出答案的表达式。观察 + 暴力拆狮子。

T3 超级树

题面

如果一棵树除了叶节点外每个节点都恰有两个子节点，那么称它为一棵满 二叉树。

一棵k-超级树可按如下方法得到：取一棵深度为k的满二叉树，对每个节 点，向它的所有祖先连边（如果这条边不存在的话）。例如，下图是一个4-超 级树的例子：

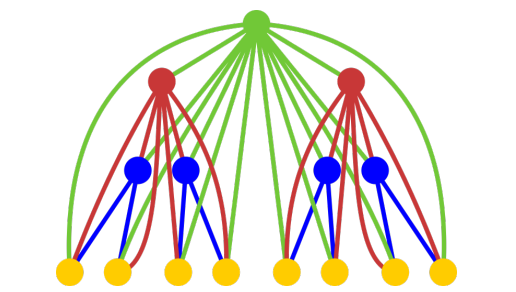
image

现在你的任务是统计一棵k-超级树中有多少条每个节点最多经过一次的不 同有向路径。两条路径被认为不同，当且仅当它们经过的节点的集合不同，或 经过的节点的顺序不同。由于答案可能很大，请输出总路径数对mod取模后的 结果。

解析

灵魂 DP

这满二叉树、这点集不同，这不就是给组合准备的吗？然后想了一个小时，果断放弃🤡。

DP 组合不分家。按理来说，像这种题，不是组合肯定就是 DP 了。

我们设鬼能想到的 \(dp[i][j]\) 表示在一棵 \(i\) 超级树里，有 \(j\) 条路径同时存在，并且这 \(j\) 条路没有公共点时，可能的情况数。

离谱。比如说这个 2-超级树。

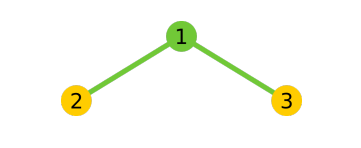
image

\(dp[2][1]=9\)，分别为 \((1),(2),(3),(12),(13),(21),(31),(213),(312)\)。

\(dp[2][2]=7\)，分别为 \((1,2),(1,3),(2,3),(2,13),(2,31),(3,12),(3,21)\)。

同理 \(dp[2][3]=1\)，而 \(dp[2][4]=0\)，因为这棵树里才 \(3\)​ 个点。并且发现，我们需要的答案为 \(dp[k][1]\)。

那么如何根据已知状态更新接下来的状态呢？不难发现，满二叉树是具有可递归性的。假设当前为 \(i\)-超级树，那么 \(i+1\)-超级树的两个儿子必定是\(i\)-超级树。不妨考虑用 \(i\) 更新 \(i+1\)。

令 \(sum=dp[i][x]\times dp[j][y]\)。分为五种情况：

  • 与根节点无关，左右子树保持原样。那么在左子树里选 \(x\) 条边，在右子树里选 \(y\) 条边，那么新树里就有 \(x+y\) 条边，并且互不影响。根据乘法原理有：

    \[dp[i+1][x+y]+=sum \]

  • 现在让左子树的 \(x\) 条边里选出一条边终点与根节点相连，右子树不动，那么 \(x\) 条边里选 1 条的方案数为 \(sum\times x\) ，但考虑到边是有顺序的，终点可以连，那么起点也可以连，所以对于左子树的方案数为 \(sum\times 2x\) 。右子树同理。这里虽然连接了根节点，但是数量却未发生变化，所以有：

    \[dp[i+1][x+y]=sum\times 2(x+y) \]

  • 现在让左子树里的一条边的起点连向根节点，然后再连接右子树的一条边的终点。那么总数量就会 \(-1\)。还是那句话，路径是有向的，所以还需 \(\times 2\)。所以有：

    \[dp[i+1][x+y-1]=2sum\times x\times y \]

  • 刚才讨论了那么多左右子树的问题，但别忘了根节点本身就是一条路径：

    \[dp[i+1][x+y+1]+=sum \]

  • 考虑新加的根节点对左右子树内部的影响。考虑在左子树选出一条边起点连向根节点，然后再选出一条边连接根节点。也就是说，先选出一条边作为起点，再选出一条边作为终点。这样就会产生 \(sum\times x\times (x-1)\)的贡献。右子树同理。

    \[dp[i+1][x+y-1]+=sum\times [x(x-1)+y(y-1)] \]

至此，五种情况讨论完成，不重不漏。考虑一个问题，咱设的状态数组能否开下。一棵深度为 \(k\) 的满二叉树拥有 \(2^k-1\) 个节点，而 \(k\le 300\) 显然开不下。 那么考虑什么状态能够对 \(dp[k][1]\) 产生贡献。是 \(dp[k-1][0]\) 和 \(dp[k-1][1]\) 两种。那又是什么状态能对它俩产生贡献呢？\(dp[k-2][0]\)、\(dp[k-2][1]\) 和 \(dp[k-2][2]\) 三种。以此类堆，所以我们只需要计算出 \(dp[i][x\le k-i]\) 的状态即可。并且树的节点数也对 \(x\) 有限制作用。所以

\[x\le \min\{2^i-1,n-i\} \]

对于初始状态，令 \(dp[0][0]=1\) 即可。

code 
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define sum (ll)dp[i-1][x] * dp[i-1][y] % m
int k, m, dp[301][601]; 
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>k>>m; dp[0][0] = 1;
	for(int i=1; i<=k; ++i) for(int x=0; x<=k-i+2; ++x) for(int y=0; y<=k-i+2; ++y){
		dp[i][x+y] = ((ll)dp[i][x+y] + sum) % m;
		dp[i][x+y] = ((ll)dp[i][x+y] + (ll)sum * ((x + y) << 1)) % m;
		dp[i][x+y-1] = ((ll)dp[i][x+y-1] + (ll)sum * x * (y << 1)) % m;
		dp[i][x+y+1] = ((ll)dp[i][x+y+1] + sum) % m;
		dp[i][x+y-1] = ((ll)dp[i][x+y-1] + (ll)sum * ((x-1) * x + (y-1) * y)) % m;
	} return cout<<dp[k][1], 0;
}

T4 成绩单

题目描述

期末考试结束了，班主任 L 老师要将成绩单分发到每位同学手中。L 老师共有 \(n\) 份成绩单，按照编号从 \(1\) 到 \(n\) 的顺序叠放在桌子上，其中编号为 \(i\) 的的成绩单分数为 \(W_i\)。

成绩单是按照批次发放的。发放成绩单时，L 老师会从当前的一叠成绩单中抽取连续的一段，让这些同学来领取自己的成绩单。当这批同学领取完毕后，L 老师再从剩余的成绩单中抽取连续的一段，供下一批同学领取。经过若干批次的领取后，成绩单将被全部发放到同学手中。

然而，分发成绩单是一件令人头痛的事情，一方面要照顾同学们的心理情绪，不能让分数相差太远的同学在同一批领取成绩单；另一方面要考虑时间成本，尽量减少领取成绩单的批次数。对于一个分发成绩单的方案，我们定义其代价为：

\[a \times k + b \times \sum_{i = 1} ^ k (max_i - min_i) ^ 2 \]

其中 \(k\) 是分发的批次数，对于第 \(i\) 批分发的成绩单，\(max_i\) 是最高分数，\(min_i\) 是最低分数，\(a\) 和 \(b\) 是给定的评估参数。现在，请你帮助 L 老师找到代价最小的分发成绩单的方案，并将这个最小的代价告诉 L 老师。当然，分发成绩单的批次数 \(k\) 是你决定的。

输入格式

第一行包含一个正整数 \(n\)，表示成绩单的数量。第二行包含两个非负整数 \(a,b\)，表示给定的评估参数。第三行包含 \(n\) 个正整数，\(w_i\) 表示第 \(i\) 张成绩单上的分数。

输出格式

仅一个正整数，表示最小的代价是多少。

样例 #1

样例输入 #1
10
3 1
7 10 9 10 6 7 10 7 1 2
样例输出 #1
15

提示

\(n \leq 50\)，\(a \leq 1500\)，\(b \leq 10\)，\(w_i \leq 1000\)。

解析

for(int l=1, r=len; r<=len; ++l, ++r)

下回遇到这种情况直接重构得了🤮

一眼区间 DP，但状态没设对，还是太🥬。考场上瞬间想了个 DP，设 \(dp[l][r][k]\) 表示通过 \(k\) 次消去区间 \(l\sim r\) 所需要的最小花费。想都没想拉了一坨 dP，没想到小样例竟然过了，并且取得了高贵的 \(70pts\)。但事后想了想，很明显是假的。

假的code（场码） 
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n, a, b, res[51], dp[51][51][51], ans = LONG_MAX;
struct SquareTable{
	int mx[51][10], mn[51][10];
	inline void init(){
		for(int i=1; i<=n; ++i) mx[i][0] = mn[i][0] = res[i];
		for(int j=1; j<=__lg(n); ++j) for(int i=1; i+(1<<j)-1<=n; ++i){
			mx[i][j] = max(mx[i][j-1], mx[i+(1<<(j-1))][j-1]);
			mn[i][j] = min(mn[i][j-1], mn[i+(1<<(j-1))][j-1]);
		}
	}
	inline int QueryMx(int l, int r){
		if(l > r) return -1;
		int k = __lg(++r - l);
		return max(mx[l][k], mx[r-(1<<k)][k]);
	}
	inline int QueryMn(int l, int r){
		if(l > r) return INT_MAX;
		int k = __lg(++r - l);
		return min(mn[l][k], mn[r-(1<<k)][k]);
	}
} st;
signed main(){
	ios::sync_with_stdio(0), cin.tie(0) ,cout.tie(0);
	cin>>n>>a>>b; for(int i=1; i<=n; ++i) cin>>res[i]; st.init();
	if(b == 0) return cout<<a, 0;
	memset(dp, 0x7f, sizeof(dp));
	for(int len=1; len<=n; ++len) for(int l=1, r=len; r<=n; ++l, ++r)
		dp[l][r][1] = a + b * (st.QueryMx(l, r) - st.QueryMn(l, r)) * (st.QueryMx(l, r) - st.QueryMn(l, r));
	for(int len=2; len<=n; ++len){
		for(int l=1, r=len; r<=n; ++r, ++l){
			for(int k=2; k<=len; ++k){
				for(int lenn=1; lenn<len; ++lenn){
					for(int ln=l, rn=l+lenn-1; rn<=r; ++ln, ++rn){
//						printf("l = %lld r = %lld ln = %lld rn = %lld ", l, r, ln, rn);
						int lmx = st.QueryMx(l, ln-1), lmn = st.QueryMn(l, ln-1);
						int rmx = st.QueryMx(rn+1, r), rmn = st.QueryMn(rn+1, r);
						int mx, mn;
						if(l == ln) mx = rmx, mn = rmn;
						else if(r == rn) mx = lmx, mn = lmn;
						else mx = max(lmx, rmx), mn = min(lmn, rmn);
//						printf("mx = %lld mn = %lld\n", mx, mn);
						dp[l][r][k] = min(dp[l][r][k], dp[ln][rn][k-1] + a + b * (mx - mn) * (mx - mn));
					}
				}
			}
		}
	}
	for(int i=1; i<=n; ++i) ans = min(ans, dp[1][n][i]);
	return cout<<ans, 0;
}

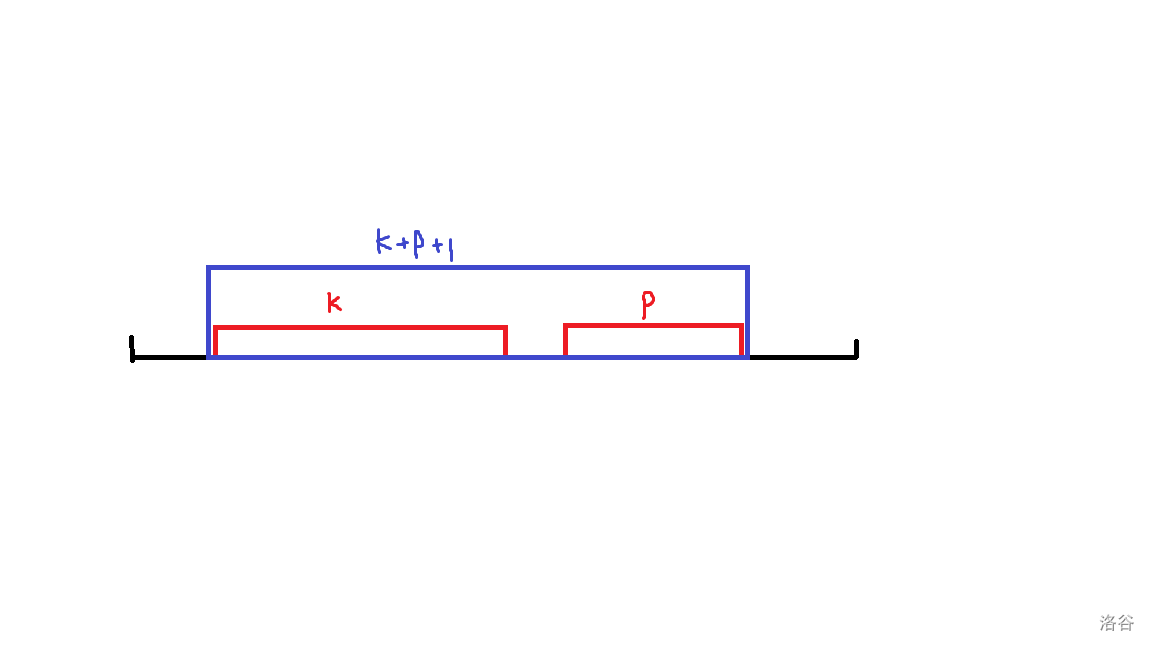
就比如这段区间，我的 dP 只能一段一段扩展，不能让次数为 \(k\) 和 \(p\) 的两个区间合并。也就是说，我的 dP 不能在一整段里扣，而是不断从两边上扣。所以是假的。数据很水。

正解

灵魂 DP

给你 \(n\le 50\) 是有原因的。我们发现 DP 状态只有 \(l\) 和 \(r\) 两个维度很难转移。所以考虑添加状态。因为每一段区间的代价只与 \(max\) 和 \(min\) 有关。所以设 \(g[l][r][mx][mn]\) 表示消去了 \(l\sim r\) 这段区间中某些部分剩下的散块中最值为 \(mx\) 和 \(mn\)，然后全部消掉（把 \(l\sim r\) 全消掉）的最小花费。设 \(f[l][r]\) 表示把 \(l\sim r\) 全消掉的最小花费。对于多状态 DP 方程，现在就需要建立两个状态之间的关系。

可以发现，对于 \(g[l][r][mx][mn]\) 的散块其实只需要一步操作就能全部消掉，所以有：

\[f[l][r]=min\{g[l][r][mx][mn]+a+b\times(mx-mn)^2 \} \]

现在考虑 \(g\) 的扩展。假设在右边加入新点 \(r+1\)。那么会有两种情况：

  • 把新点加到已经消掉的那部分里去，那么就不会对现有状态产生影响：

    \[g[l][r+1][mx][mn]=min\{g[l][r][mx][mn]+f[r][r] \} \]

    但是发现，对于 \(r\) 后面任何一个点都能满足这个转移方程，显然是需要刷表的。考虑要把区间扩展到 \(l\sim k\)，那么有：

    \[g[l][k][mx][mn]=min\{g[l][r][mx][mn]+f[r+1][k] \} \]

    不好转移？把 \(r\) 和 \(k\) 调换一下：

    \[g[l][r][mx][mn]=min\{g[l][k][mx][mn]+f[k+1][r] \} \]

  • 把新点加到没有消除的散块里去，需要更新当前状态：

    \[g[l][r+1][max(mx, a_{r+1})][min(mn,a_{r+1})]=min\{g[l][r][mx][mn] \} \]

    依旧考虑换一下：

    \[g[l][r][max(mx, a_{r})][min(mn,a_{r})]=min\{g[l][r-1][mx][mn] \} \]

至此所有转移都已完成。但，\(a\) 的范围有点大，需要离散化。复杂度 \(\mathcal{O}(n^5)\)。

code 
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n, a, b, res[51], pos[51], g[51][51][51][51], f[51][51];
signed main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n>>a>>b; for(int i=1; i<=n; ++i) cin>>res[i], pos[i] = res[i];
	sort(pos+1, pos+1+n); int cnt = unique(pos+1, pos+1+n) - pos - 1;
	for(int i=1; i<=n; ++i) res[i] = lower_bound(pos+1, pos+1+cnt, res[i]) - pos;
	memset(f, 0x3f, sizeof(f)), memset(g, 0x3f, sizeof(g));
	for(int i=1; i<=n; ++i) f[i][i] = a, g[i][i][res[i]][res[i]] = 0;
	for(int len=2; len<=n; ++len) for(int l=1, r=len; r<=n; ++l, ++r){
		for(int mx=1; mx<=cnt; ++mx) for(int mn=1; mn<=mx; ++mn)
			g[l][r][max(mx, res[r])][min(mn, res[r])] = min(g[l][r][max(mx, res[r])][min(mn, res[r])], g[l][r-1][mx][mn]);
		for(int mx=1; mx<=cnt; ++mx) for(int mn=1; mn<=mx; ++mn){
			for(int k=l; k<r; ++k) g[l][r][mx][mn] = min(g[l][r][mx][mn], g[l][k][mx][mn] + f[k+1][r]);
			f[l][r] = min(f[l][r], g[l][r][mx][mn] + a + b * (pos[mx]-pos[mn]) * (pos[mx]-pos[mn]));
		}
	} return cout<<f[1][n], 0;
}
posted @ 2024-08-10 21:42  XiaoLe_MC  阅读(13)  评论(0)  编辑  收藏  举报