[学习笔记] 树上差分 - 图论

前置知识：树，LCA，前缀和与差分

边差分

这个名字是在网上看到的，不理解为什么要叫这么一个名字，可能是因为它与 树链修改 有关。当然，用于 树链修改 单点查询 非常方便~

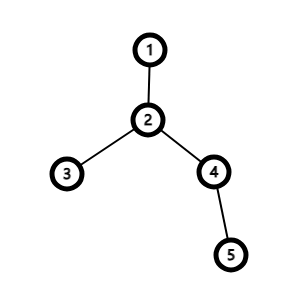
看这个图，该图是以点1为根进行DFS的。如果我们要把从3 -> 4这条树链上所有的点统统加上1，可以都转化为对到根节点的树链的操作，我们可以把3 -> 1全加上1，4 -> 1全加上1，发现2多加了1，1多加了2，所以2 - > 1减掉1，1 -> 1减掉1。这并不难想。但是如何实现把某一结点到根节点上所有的点进行权值加减呢？

联想到差分，我们可以分树链差分，对于3 -> 1链上的点，将这条链的开始(节点3)+1，将这条链的末尾(节点0)-1，最后查询时，把这个节点的子节点权值和自身权值相加即为最终权值。

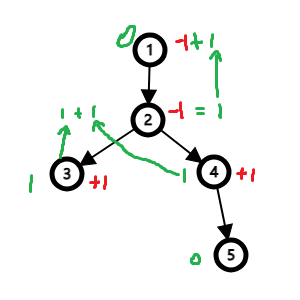
画图太难用了！

树链修改 单点查询

看一道例题：[JLOI2014] 松鼠的新家

一道典型的树链修改 单点查询 + LCA题目。需要注意，我们在对每段路径进行操作的时候，前一个路径的尾端点与后一个路径的首端点多放了一个糖果，而且，最后一段路径的右端点是不用放糖果的，所以要统统减掉。

#include<bits/stdc++.h>
using namespace std;
#define min(x,y) (in[x]<in[y])?x:y
const int N = 3e5 + 1;
int n, ord[N], in[N], st[19][N], tot, w[N];
vector<int> G[N];
bitset<N> flag;
inline void dfs1(int k, int fa){
	st[0][in[k] = ++tot] = fa;
	for(int v : G[k]) if(!in[v]) dfs1(v, k);
}
inline void dfs2(int k){
	flag[k] = 1;
	for(int v : G[k]) if(!flag[v]) dfs2(v), w[k] += w[v];
}
inline int lca(int a, int b){
	if(a == b) return a;
	if((a = in[a]) > (b = in[b])) swap(a, b);
	int k = __lg(b-a++);
	return min(st[k][a], st[k][b-(1<<k)+1]);
}
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin>>n;
	for(int i=1; i<=n; ++i) cin>>ord[i];
	for(int i=1, a, b; i<n; ++i){
		cin>>a>>b;
		G[a].push_back(b), G[b].push_back(a);
	}
	dfs1(1, 0);
	for(int i=1; i<=__lg(n); ++i)
	for(int j=1; j<=n-(1<<i)+1; ++j)
		st[i][j] = min(st[i-1][j], st[i-1][j+(1<<i-1)]);
	for(int i=1; i<n; ++i){
		int a = ord[i], b = ord[i+1];
		int fa = lca(a, b);
//		printf("lca(%d, %d) = %d\n", a, b, fa);
		++w[a], ++w[b], --w[fa], --w[st[0][in[fa]]];
	}	
	dfs2(1);
	for(int i=1; i<=n; ++i){
		if(i != ord[1]) --w[i];
		cout<<w[i]<<'\n';
	}
	return 0;
}

树链修改 子树和查询

再来看这道题DFS 序 3，树上差分 1

主要用到边差分思想，类比树状数组区间修改区间查询，将子树和用差分数组表示出来即可。

需要维护两个树状数组，\(t1\) 维护 \(w_i\) ，\(t2\) 维护 \(deep_i*w_i\)。

树链修改即为( \(l=lca(a,b)\) \(f=fa(l)\))：

\( w_a+k\ \ w_b+k\ \ w_l-k\ \ w_f-k \)

查询单点为：

\( query1(out[a])-query1(in[a]-1) \)

查询子树和即为:

\( query2(out[a])-query2(in[a]-1)-\\ (deep[a]-1)*(query1(out[a])-query1(in[a]-1)) \)

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) ((x)&(-x))
#define min(x,y) in[x]<in[y]?x:y
#define ll long long
const int N = 1e6 + 1;
int n, m, r, lg[N], w[N], st[20][N], in[N], out[N], cnt;
ll t1[N], t2[N], deep[N];
vector<int> G[N];
inline ll rd(){
	ll x = 0, f = 1;
	char ch = getchar();
	while(ch<'0' || ch>'9') f = ch='-'?-1:1, ch = getchar();
	while(ch>='0' && ch<='9') x = (x<<1) + (x<<3) + (ch^48), ch = getchar();
	return x*f;
}
inline void wt(ll k){
	if(k<0) putchar('-'), k=-k;
	if(k/10>0) wt(k/10);
	putchar(k%10 + '0');
}
inline void modify1(int k, ll w){
	if(!k) return;
	for(int i=k; i<=n; i+=lowbit(i)) t1[i] += (ll)w;
}
inline void modify2(int k, ll w){
	if(!k) return;
	for(int i=k; i<=n; i+=lowbit(i)) t2[i] += (ll)w;
}
inline ll query1(int k){
	if(!k) return 0ll;
	ll ans = 0ll;
	for(int i=k; i>0; i-=lowbit(i)) ans += t1[i];
	return ans;
}
inline ll query2(int k){
	if(!k) return 0ll;
	ll ans = 0ll;
	for(int i=k; i>0; i-=lowbit(i)) ans += t2[i];
	return ans;
}
inline void dfs(int k, int f){
	st[0][in[k] = ++cnt] = f;
	modify1(in[k], w[k]), modify1(in[f], -w[k]);
	modify2(in[k], w[k]*deep[k]), modify2(in[f], -w[k]*deep[f]);
	for(int v : G[k]) if(!in[v]) deep[v] = deep[k]+1, dfs(v, k);
	out[k] = cnt;
}
inline int lca(int a, int b){
	if(a == b) return a;
	if((a = in[a]) > (b = in[b])) swap(a, b);
	int k = lg[b-a++];
	return min(st[k][a], st[k][b-(1<<k)+1]);
}
signed main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	n=rd(), m=rd(), r=rd();
	lg[0] = -1;
	for(int i=1; i<=n; ++i){
		lg[i] = lg[i>>1] + 1;
		w[i]=rd();
	}
	for(int i=1, a, b; i<n; ++i){
		a=rd(), b=rd();
		G[a].push_back(b), G[b].push_back(a);
	}
	deep[r] = 1, dfs(r, 0);
	for(int i=1; i<=lg[n]; ++i)
	for(int j=1; j<=n-(1<<i)+1; ++j)
		st[i][j] = min(st[i-1][j], st[i-1][j+(1<<i-1)]);
	for(int i=1, a, b, opt; i<=m; ++i){
		ll c; opt=rd(), a=rd();
		if(opt == 1){
			b=rd(), c=rd();
			int fa = lca(a, b);
			modify1(in[a], c), modify2(in[a], c*deep[a]);
			modify1(in[b], c), modify2(in[b], c*deep[b]);
			modify1(in[fa], -c), modify2(in[fa], -c*deep[fa]);
			modify1(in[st[0][in[fa]]], -c), modify2(in[st[0][in[fa]]], -c*deep[st[0][in[fa]]]);
		}else if(opt == 2) wt(query1(out[a]) - query1(in[a]-1)), putchar('\n');
		else wt(query2(out[a]) - query2(in[a]-1) - (deep[a]-1)*(query1(out[a]) - query1(in[a]-1))), putchar('\n');
	}
	return 0;
}