教学班级:005?(周三上午三四节)
项目地址:git@github.com:bingokunkun/rg-homework1.git
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 200 | 240 |
| · Design Spec | · 生成设计文档 | 30 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 10 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 40 | 40 |
| · Coding | · 具体编码 | 30 | 30 |
| · Code Review | · 代码复审 | 30 | 40 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 200 | 240 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 20 | 20 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 40 | 50 |
| - | 合计 | 640 | 730 |
解题思路
- 看到题目之后首先想到的就是把所有的点算出来,然后依次比较查重。
- 第一步当然是记录所有直线的信息了。为了避免出现浮点数,我将直线用如下公式表示:
\[y={\frac{kup}{kdown}}x+{\frac{bup}{bdown}}
\]
- 因此需要存储四个数组:kup、kdown、bup、bdown,为了能让之后的工作稍微简单一点,需要对k和b的分数形式化简,即提取公因子,使用gcd()函数完成。
- 第二步就是判断两条直线的关系了,由于之前已经进行了化简,因此在这里只需要比较kup和kdown是否相等即可判断是否平行,若平行则无交点,若不平行则有一个交点,此时将交点坐标:
\((\frac{xup}{xdown},\frac{yup}{ydown})\) 存储下来。 - 最后一步遍历交点坐标数组,计算不相同的点数即可
设计过程
- 根据解题思路,除了主函数外,一共有三个函数,分别行驶着读取数据(getInput)、求最大公因数(gcd)、分析交点数的功能(handle)。
- 其中,主函数调用getInput和handle,该二者调用gcd。
- 模块测试:
gcd:简单手动测试,随机输入数字,判断正误。
getInput:对于计算好的kup、kdown、bup、bdown,将原数据x0、y0、x1、y1带入到直线公式中,判断结果是否为零。
handle:将计算好的xup、xdown、yup、ydown带入到两条直线中,判断该点是否在直线上即可。
改进过程
- 直线信息时一定要记录的,但是最开始的记录方法需要经过大量的计算,而且溢出的可能性较大。因此,后期我才用了直接记录x0,x1-x0,y0,y1-y0的方式,一来不会溢出,二来方便以后的计算。同时gcd函数可用可不用了。
- 在更改了上述存储结构之后,发现在进行多次乘法之后,只需要进行一次除法即可算出坐标,那么便可以使用double类型的浮点数记录点的坐标。
- 更改了点坐标的存储方式之后,发现四元组变成了二元组,使用哈希映射更加方便,同时速度会更加快捷,于是采用unordered_map的嵌套形式避免重复。
- 后来发现了更好的形式,使用pair<double,double>的方式存储点坐标,置于set容器当中(让set内置的方法自由翻滚)。
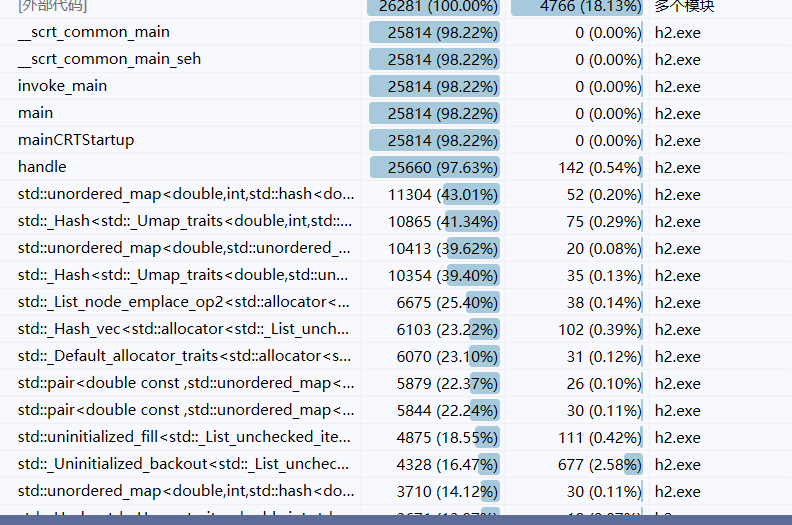
图为一次性能分析,其中handle函数浪费的时间最长

上图数据是随机生成的40000条直线,其中构造了大量的平行直线,可见,在判断是否平行这一处语句浪费的资源最多。当没有精心构造的大量平行时,则为pointSet的insert函数最多。
代码说明
void handleLL() {
long long xu, xd, yu;
for (int i = 0; i < num; i++) {
for (int j = i + 1; j < num; j++) {
xd = (long long)b[j] * d[i] - (long long)b[i] * d[j];
if (xd == 0) {
continue;
}
xu = (long long)b[j] * ad_bc[i] - (long long)b[i] * ad_bc[j];
yu = (long long)d[j] * ad_bc[i] - (long long)d[i] * ad_bc[j];
double px, py;
px = (double)xu / xd;
py = (double)yu / xd;
pair<double,double> p = make_pair(px, py);
pointSet.insert(p);
}
}
}
- 此处为整个程序中最关键的一环,abcd分别记录了x0,x1-x0,y0,y1-y0,ad_bc记录的是ad-bc的值,纯属是方便计算。现在想要计算直线i和直线j之间的交点坐标(px,py),通过数学推导可以计算得到xu,yu,xd。其中,若xd为零,则ij两条直线平行,没有交点;若不为零则可以计算得到坐标的值(px,py)将其存储在set容器当中,最后输出pointSet的大小即可。


