作业要求<->目录
(1)梳理JML语言的理论基础、应用工具链情况<->JML总结
(2)部署SMT Solver<->无
(3)部署JMLUnitNG/JMLUnit<->测试
(4)梳理架构设计分析对架构的重构<->数据结构+核心思想+算法
(5)按照作业分析代码实现的bug和修复情况<->测试
(6)阐述对规格撰写和理解上的心得体会<->最后总结
JML总结
JML(Java Modeling Language)是在Java代码中增加的一些符号,这些符号用来表示一个方法是干什么的,却并不关心它的实现。使用JML让我们就能够描述一个方法的预期的功能而不需要考虑如何实现。通过这种方式,JML把过程性的思考延迟到方法设计中,从而扩展了面向对象设计的这个原则。
JML引入了大量用于描述行为的结构,比如有模型域、量词、断言可视范围、预处理、后处理、条件继承以及正常行为(与异常行为相对)规范等等,这些结构使得JML非常强大。
JML关键字requires用来表示前置条件,前置条件表示调用一个方法前必须满足的一些要求。一个方法的后置条件规范表示一个方法的责任,也就是说当这个方法返回时,它必须满足这个后置条件的要求。模型域类似于成员变量,它只能被应用到行为规范中。用JML定义行为规范的时候不需要考虑执行效率,程序运行时JML断言检查却是很重要的。所以开启断言检查时程序的运行可能会有性能的压力。
作业浅析
这次作业相对于之前两个单元来说,个人感觉是比较容易的,不需要考虑太多复杂的情况,也没有很迷的多线程debug。各个函数基本上规格已经给出的很详细了,我就只列出我自己设定的变量和所用的数据结构。如下图所示(第三次作业)
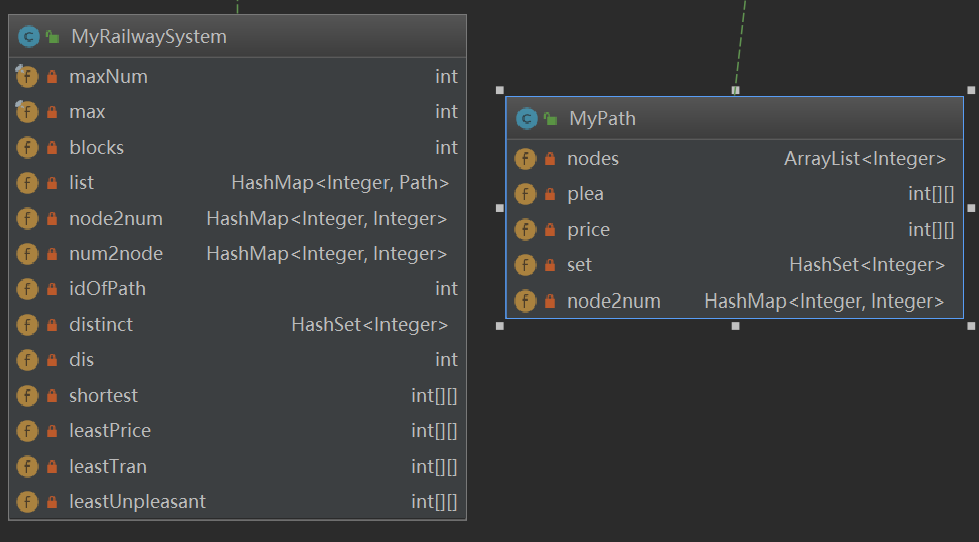
数据结构(与重构)
1.hashmap的嵌套(第一、二次)
在c语言中,本次作业所使用的数据结构可以很好的通过邻接链表来存储,然而Java中没有指针,因此我最先想到的可以采取的数据结构就是采用hashmap的嵌套,这样不但能够直接找到每一个Edge的权值,还能提高查找的速度。
2.二维int数组(第三次)
Hashmap的嵌套确实能够完成这次作业的要求,也正是如此,我的第一次第二次作业都是使用该数据结构完成的。然鹅,在第三次作业中,由于很难使用我最拿手的BFS算法来实现计算,使用其他算法时hashmap的嵌套写来写去导致代码量激增,而且十分难看。查找起来也比较费劲,一不小心又会出现内层hashmap的无效访问导致异常。因此我果断(艰难)抛弃了hashmap的思路,使用二维数组来存储,最重要的问题就是二维数组只能是连续的存储,因此在MyRailwaySystem类中出现了node2num和num2node两个hashmap类型进行转换,把不连续的点映射成连续的点,便于二维数组的存储,与此同时,所有的函数传送进来的node全部进行转化,变成二维数组对应下标。
3.hashset
Hashset完全是一个用来判断不同节点数的数据类型,从distinct一名也可以看出,每当有新的path进入时,就会把所有的点全部存入hashset,最后只要获取hashset的size就能得到不同的点数,同时在更新二维数组的时候也就有了更明确的范围。
核心思想(与重构)
这几次作业的难点主要在最短路径上,换成、票价、不满意度基本上是同一种类型,而其他的一些函数则是用心一点就不会出现问题。因此,下面我主要介绍一下我做这单元作业时,关于最短路径等四个比较困难的问题上的想法。
1.空间换时间
在第一次写这个单元的作业时,我首先想到的就是每次查找一次最短路径时,就在全图使用BFS查找一次,这个想法确实很简单,当我写完之后交上去时间当然远远没有超。
但是,每一次查找都要全图BFS一次,很耗费时间,不如把已经查出来的存起来,下次再查找的时候不就能直接得到结果并输出了吗?于是,空间换时间的第一次修改诞生了。
然而,通过对BFS的深入理解,我们可以很容易地发现,BFS从某一结点出发,当权值相等时,每个第一次遇到的结点都是最短路径。因此,一次BFS其实是可以找到一个点到所有点的最短路径,那为什么不把他们全部都存起来呢?于是,空间换时间的第二次修改诞生了。
再后来,既然节点数那么少,查找指令又那么多,那还不防直接全部存起来来得简单,于是,最终版诞生了,同时也确定了之后每次作业我都会在add或remove一条path之后直接计算出所有想要的结果。
2.双向存储换单向存储(第二次)
最初我是觉得双向存储比较省时间的,打个比方:从1到2的最短路径我算出来了是10,那么我在对1进行BFS遍历时就已经得到了2到1的最短路径,不如就直接把1到2和2到1全部存起来,那么在对2进行BFS遍历时,就可以直接跳过1,不需要存储了。理想很丰满,现实是当对2进行BFS时,还要进行一次判断,在两次插入的基础上又多了一次判断,还不如当初只是单项存储来的快,代码量也是原来的三分之一。时间经过测试,700ms左右的数据可以节省40ms左右。
3.最短路径与最少换乘的结合(第三次)
我觉得这个想法是本单元第三次作业最核心的想法,虽然有同学提出了拆点的做法,但我还是觉得这个想法绝妙至极。
通俗来说我们可以把最少换乘问题进一步变成最少乘车数的问题,假设一次旅行一共做了x辆车,那么显然的换乘次数就是x-1,于是只需要将每一条路径上的任意两个点用一条全职为1的边链接起来,那么再使用BFS等各种花里胡哨的算法就能轻易完成最少换乘的计算。
相对来说最少票价和不满意度的计算则是前两者的合成。以最少票价为例:
最少票价price=最短路径x+最少换乘y*2,
定义:每一辆车上的花费p=在这条路径上的最短路径x+2
按照之前的想法,y=y+1-1。则可以将在每一辆车上的最短路径分离开,加上乘车的票价2,即可得到在每一辆车上花费的价钱。那么:
Price=p1+p2+p3+……pn-2
显然p1,p2等我们可以在每一条path刚刚添加上去的时候计算出来,这也是为什么MyPath类中出现了两个二维数组的原因。剩下的就好办许多了,不满意度和票价的计算如出一辙,只需要使用各种算法进行计算就好了。
算法(与重构)
1.BFS(第一次)
BFS算法可谓是计算权值相同的图时,最简单最快速的算法(可能有之一?)了。在BFS逐渐扩充功能之后(即记录起点到每一个结点的最短路径),简直强到爆炸。前两次作业中BFS完全不在话下。然而在最少票价和最少不满意度的计算时,BFS的神通就没了,因此只能寻找其他的有权值的算法。
2.dijkstra
Dij算法也是本次作业中听说的最频繁的名词之一,较低的复杂度相较其他算法更胜一筹,但是由于写起来比较麻烦,四个dij算的也比较烦,因此,我在第三次作业中并没有使用该方法,而是采用了floyd算法。
3.Floyd(第三次)
显然Floyd没有dij快,但是书写起来极其简单规范,代码赏心悦目,而且最重要的是,四个Floyd可以一起跑,而且不需要反复初始化!而且如果有必要的话Floyd其实也可以优化的。在第三次作业中,我在每一条path里使用了一次Floyd,又在总图里使用了Floyd,写起来非常顺手,而之所以没有采用floyd+BFS的主要原因就是一次遍历算出4个结果,使用其他算法就会失去一起跑的优势。
4.prim
这是我见到的一位同学使用的方法,吹爆!!
从一个顶点a出发寻找到与其相邻的所有结点,并将a到这些节点的最短路径记录下来,找到其中最小的,显然全图中没有另一条路径能够比这条更短,将其加入到已经计算好的节点中去,并找到与其相邻的所有点,计算x到他们的最短路径,再次寻找到最小的那一条,记录……
也就是说,将Prim算法的记录值变成了从起点开始的最短路径,其他完全相同。该算法计算时和dij近乎相同,但是省去了初始化的大量时间,简直强无敌。
测试
本单元学习了Junit之后,发现他确实是一个很好用的工具,第一次由于我改了几次实现方法,在后来并没有采用Junit,而是和自己之前写的程序对拍(然而没有拍出不同),接着和同学对拍,才发现了问题所在(规格更新了)。
后来在第三次作业中我首次尝试了使用Junit,然而结果是这样的:
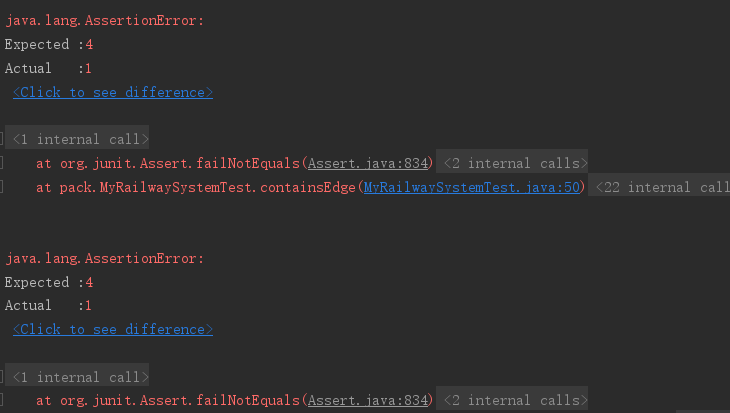
是这样的:
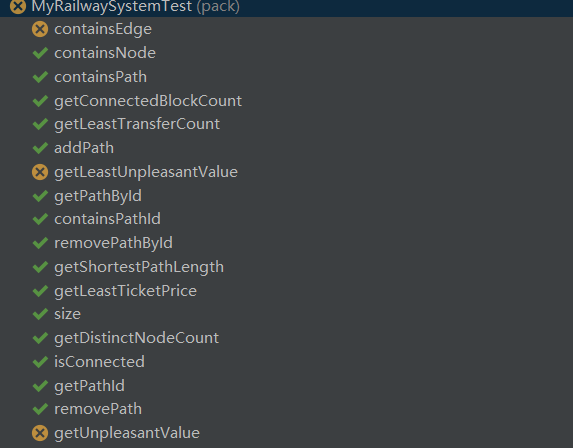
经过修debug后发现了一个比较重大的问题,最少不满意度和最少票价的计算其实都是有问题的,例如出现下述数据时:
PATH_ADD 1 2 3 4 5 6 7 8
PATH_ADD 2 4
PATH_ADD 4 6
由于单一路径的最短路径没有预先计算出来,而是在总图里跑了一遍,导致票价和不满意度出现bug,于是才尝试将单一路径的计算在Path类里完成。
另外,由于重构了一遍,整体数据结构出现了翻天覆地的变化。新的containsEdge忽略了一种情况,在没有该节点时,containsEdge也会出现错误,于是才进行修改,将path类作为计算票价和不满意度的类。
最后总结
通过这个单元,我第一次认识了什么是规格,并能够看懂它,通过它的要求完成代码。对面向对象函数的封装有了更加深刻的印象,一个函数就是实现一个功能,绝不拖泥带水。另外,第三次作业也令我意识到了自己在算法方面的不足,有待提高!


