64匹马8个跑道最少需要多少轮才能选出最快的4匹马?
这是在网上见到的一道腾讯面试题
先说结论:
1. 计时的情况下需要比赛8轮;
2.不计时的情况下最少需要10轮,最多需要11轮。
1 用秒表计时的话,64匹分8组。 8轮就出来了
2:不能计时的情况下
先说下思路:
一:把64匹马分8组,各跑一次,然后淘汰掉每组的后四名,这里淘汰后四名是因为只需要跑的最快的四匹马。(花费8轮);
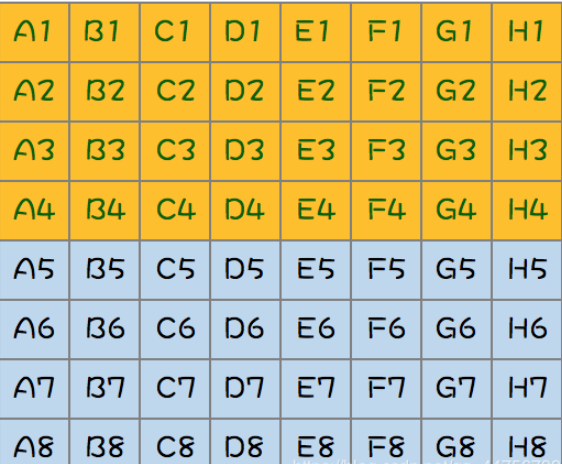
二:取每组第一名进行一次比赛,然后淘汰最后四名所在组的所有马,因为后四名所在的组的第一名没有跑过前四名的马,所以可以直接淘汰。(+1轮);
还剩16匹,第一名已经出来了
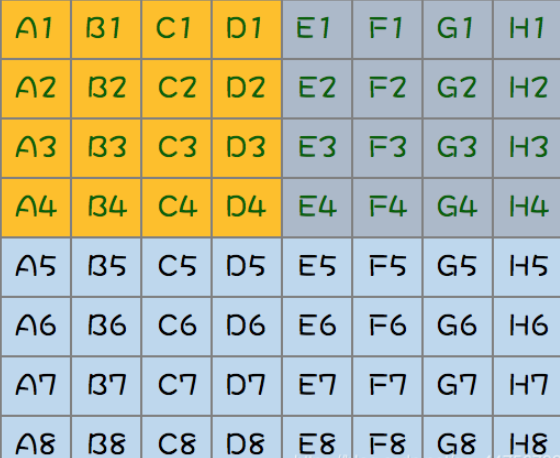
这时候还剩下16匹马,在这里其实可以继续淘汰,因为D1是第九轮的第四名,但D1又是它3所在组的第一名,那么对应的D2,D3,D4都可以继续淘汰掉。
但是第四名也可能出现在C2中,C2是所在组的第二名,那么C3,C4也可以淘汰了,同理,可以得到B4也可以淘汰了。到此为止还剩10匹马,其中A1是64匹马中跑的最快的马,可以直接晋级。如下图,其中有红色斜线是已经被pass的:
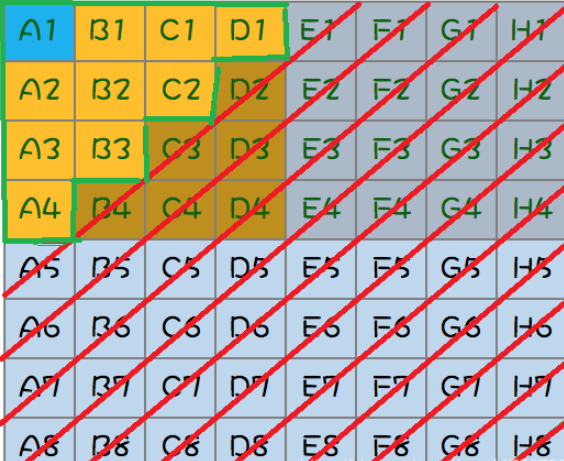
第三:
A2、A3、A4、B2、B3、C1、C2、D1八匹马跑一次,即:在剩下需要排名的马中,除了B1外,其它8匹马跑一次(+1轮)
分类讨论:
1、如果这次排名,B2或C1能进前三名,则加上B1后,B1一定能进前三名,因为B1 排名比B2和C1都要靠前;
到此比赛可以结束了;这种情况8+1+1=10次出结果;
2、如果这次排名,B2或C1不能进入前三名,则需要再进行一次比赛,B1、A2、A3、A4进行,取前三名:
这种情况8+1+1+1=11次出结果。
结论:
1. 计时的情况下需要比赛8轮;
2.不计时的情况下最少需要10轮,最多需要11轮。
参考:



