判断有向图中是否存在环

题目来自207. 课程表 - 力扣（LeetCode） (leetcode-cn.com)。

有n个课程，分别为0~(n-1)。给你二维数组arr，arr[i]=[a,b]，表示要学习a课程必须先学习b课程，其中a,b是0~(n-1)之间的数。返回是否能完成所有的课程，如果能，返回true，否则返回false。

arr[i]=[a,b]，即a-->b，把所有的指向关系表述出来就是一幅有向图，而一旦图中存在环，则没有办法完成环中课程的学习。例如下面的图片，要想学习b课程，得先学a课程，而学c课程之前必须学b课程，于是矛盾了，没有办法学习a,b,c中的任意一门课程。

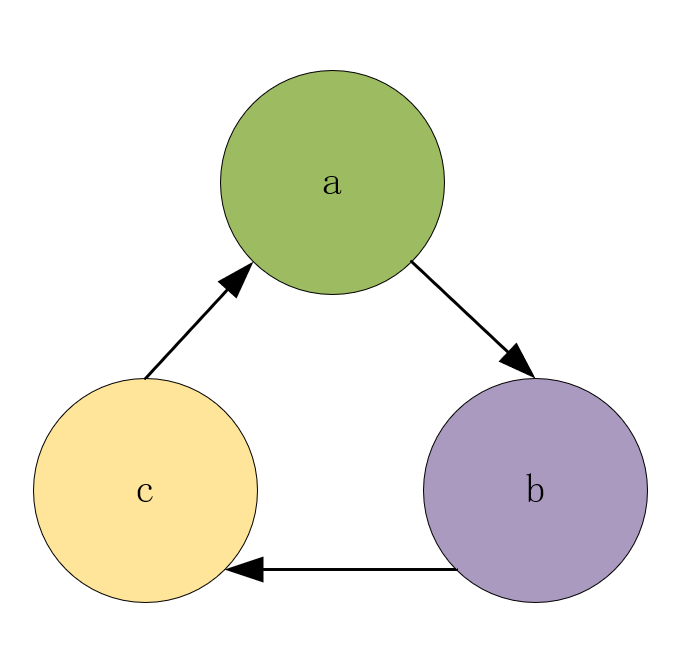
如何利用程序来实现这个问题呢？对于每个节点来说，有入度和出度两个概念，入度就是别的节点指向此节点的有向边数量，出度就是由此节点而出指向别的节点的有向边数量。可以发现，最先可以开始的课程一定是那些入度为0的节点。我们将入度为0的节点加入到队列中，每次它被弹出，说明此课程已经上完了，这时更新此节点的下一个节点的入度信息，即减1。如果更新后的下一个节点的入度为0，说可以学习此课程，于是将此节点加入队列。照着这个思路，我们就可以计算出能够学习的课程，代码思路如下，参考了力扣官方的解答。

    public boolean canFinish(int numCourses, int[][] prerequisites){
        int[] count = new int[numCourses];//记录每个节点的入度情况
        List<Integer>[] next = new List[numCourses];//记录每个节点的下一个节点
        for (int i = 0; i < numCourses; i++) {
            next[i] = new ArrayList<>();
        }
        for (int[] p : prerequisites) {
            int now = p[0],pre = p[1];
            count[now]++;//入度加1
            next[pre].add(now);//pre的下一个节点是now
        }
        Queue<Integer> queue = new ArrayDeque<>();
        for (int i = 0; i < numCourses; i++) {
            if(count[i]==0) queue.add(i);//将入度为0的节点
        }
        int n = 0;//能够学习到的课程数量
        while(!queue.isEmpty()){
            int i = queue.poll();//i表示课程
            n++;//表示学完了,完成数量加1
            for (Integer nextPoint : next[i]) {
                count[nextPoint]--;//入度减1
                if(count[nextPoint]==0) queue.add(nextPoint);
            }
        }
        return n==numCourses;
    }

上面的代码用的是广度优先搜索，如果想用深度优先搜索解决这个问题的话，请参考力扣官方解答（上方链接）。