动态规划

题目来自剑指 Offer II 100. 三角形中最小路径之和 - 力扣（LeetCode） (leetcode-cn.com)，经典的动态规划题。

题目是这样的，给你一个三角形（triangle），第一层有一个元素，第二层有两个元素，第n层有n个元素。从第i层第j个元素（arr[i][j]）走到第i+1层只有两个可选位置，即第i+1行的j位置（arr[i+1][j]）或j+1位置(arr[i][j+1])。要求你从第一层开始出发，到达最底层（第n层），要求走过的元素之和最小，并返回最小的元素和。

参考力扣官方的解答，采用动态规划的形式，用空间换时间。使用动态规划最关键的地方就是找出递推关系式，该问题中，可以看出递推关系式存在与上下两层之间。定义一个n行n列的矩阵dp,dp[i][j]的含义是到达第i行j位置所经过的元素的最小和，于是关系式为dp[i][j]=min(dp[i-1][j],dp[i-1][j-1])+triangle[i][j]。但是，在编程时有两个地方会出现问题，那就是每一行的首、末位置仅有一个来源，并非是两个来源，如下图中的1、2、3、4和6号元素。

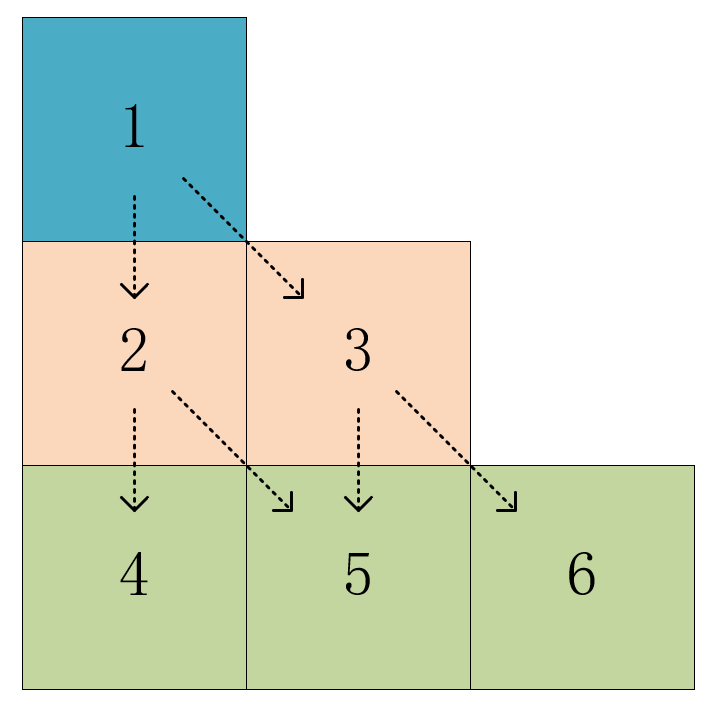
编程时需要注意的两点：1、dp[0][0]要初始化为triangle[0][0]；

　　　　　　　　　　　2、注意每一行的首、末两个元素需要单独处理。代码如下：

    public int minimumTotal(List<List<Integer>> triangle) {
        /**
         * likou-剑指offer-100
         *      答案使用的是动态规划，是用空间换时间
         */
        int n = triangle.size();
        int[][] dp = new int[n][n];//dp[i][j]表示到triangle[i][j]的最小路径和,dp[i][j]=min(dp[i-i][j],dp[i-1][j-1])+triangle[i][j]
        dp[0][0] = triangle.get(0).get(0);
        for(int i = 1;i<n;i++){
            dp[i][0] = dp[i-1][0]+triangle.get(i).get(0);//每一行的第一个元素
            for (int j = 1; j < i; j++) {
                dp[i][j] = Math.min(dp[i-1][j],dp[i-1][j-1])+triangle.get(i).get(j);
            }
            dp[i][i] = dp[i-1][i-1]+triangle.get(i).get(i);
        }
        int res = dp[n-1][0];
        for (int i = 1; i < n; i++) {
            res = Math.min(res,dp[n-1][i]);
        }
        return res;
    }

 上述的代码中使用了n*n的空间(int[][] dp = new int[n][n])，但仔细观察可以发现可以发现dp的第i行只和上一行（i-1）有关，因此，我们可以用2*n的空间（int[] dp = new int[2][n]）来模拟第i行和第i-1行，第0行充当三角形的第1、3、5...层，第1行充当第2、4、6...层。代码如下：

    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        int[][] dp = new int[2][n];//这两行交替充当第i行
        dp[0][0] = triangle.get(0).get(0);
        for(int i = 1;i<n;i++){
            int currLine = i % 2;
            int prevLine = 1 - currLine;
            dp[currLine][0] = dp[prevLine][0]+triangle.get(i).get(0);//每一行的第一个元素
            for (int j = 1; j < i; j++) {
                dp[currLine][j] = Math.min(dp[prevLine][j],dp[prevLine][j-1])+triangle.get(i).get(j);
            }
            dp[currLine][i] = dp[prevLine][i-1]+triangle.get(i).get(i);
        }
        int resAtLine = (n-1) % 2;//假设有3行，那么第0行充当第1、3层，第1行充当第2层，所以n层的结果在第(n-1)%2行中
        int res = dp[resAtLine][0];
        for (int i = 1; i < n; i++) {
            res = Math.min(res,dp[resAtLine][i]);
        }
        return res;
    }

这还不是空间优化的极致，还可以只消耗1*n的空间(int[] dp = new dp[n])来解决这个问题，但是一定要递减的枚举i，代码如下：

    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        int[] dp = new int[n];
        dp[0] = triangle.get(0).get(0);
        for(int i = 1;i<n;i++){
            dp[i] = dp[i-1]+triangle.get(i).get(i);
            for(int j = i-1;j>0;j--){
                dp[j] = Math.min(dp[j-1],dp[j])+triangle.get(i).get(j);
            }
            dp[0] = dp[0]+triangle.get(i).get(0);
        }
        int res = dp[0];
        for (int i = 1; i < n; i++) {
            if(dp[i]<res){
                res = dp[i];
            }
        }
        return res;
    }

上述代码的思路完全来自力扣官方，自己只是敲了一遍并做了记录而已。第一个代码最容易理解，但内存消耗高。第三个代码最难理解，不推荐。感觉第二个最好。