线段树和zkw线段树
作者作为一个蒟蒻,也是最近才自学了线段树,不对的地方欢迎大佬们评论,但是不要喷谢谢
好啦,我们就开始说说线段树吧
线段树是个支持区间操作和查询的东东,平时的话还是蛮实用的
下面以最基本的区间加以及查询区间和为例
线段树顾名思义就是棵树嘛,叶子节点是每个基本点,它们所对应的父亲就是它们的和,具体如下图
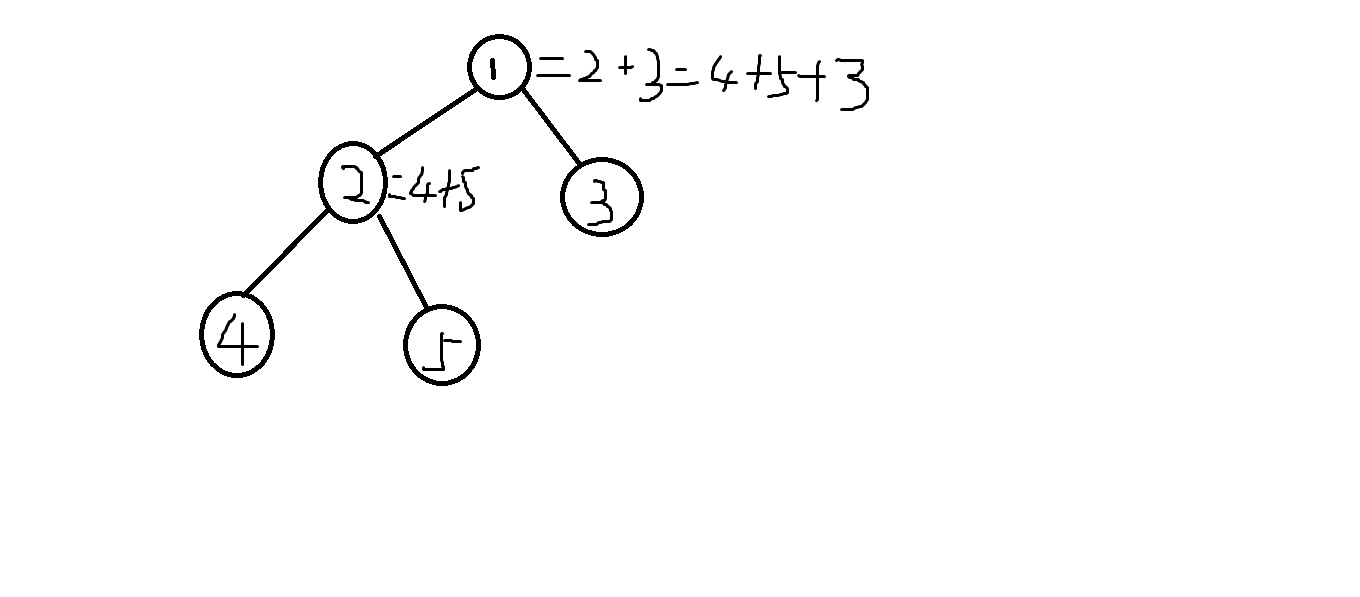
但是对于这样的线段树来说,操作所需的时间是远达不到我们的要求的(会被t),因为我们会进行一些不必要的操作,就像如果没有查询到某个点,那么就没有必要去修改这个点的值,为此,我们会引入一个懒标记,记录每个基本点需要被加上的值(称为add),那么树上任意一个点需要增加的值=该点对应的区间长度*add
那么总的来说,线段树的基本操作我个人认为可以分成3个,建树、修改和查询,当然如果继续细分也是口以(可以)的,就比如说还可以分出 区间和的向上传递(父亲节点等于子节点的和)和懒标记的向下传递(子节点的懒标记=原来的懒标记+父节点的懒标记)
所以接下来我们就来看看建树、修改和查询这3部分的具体代码吧(深呼吸)
首先是建树(build)
#define ls 2*rt,l,(l+r)/2 //left son #define rs 2*rt+1,(l+r)/2+1,r //right son #define ll long long void build(ll rt,ll l,ll r)//rt是当前点,l和r代表l到r区间的和 { if(r==l) //也就是说,我们找到了一个叶子节点,自己到自己的和 就是自己嘛 { scanf("%lld",&su[rt]);//那我们就输入这个节点的值 } else//否则就去看看当前点的左右儿子 { build(ls);//看左儿子 build(rs);//看右儿子 //当rt的左右儿子都准备好了,我们就可以求出rt的值了 su[rt]=su[2*rt]+su[2*rt+1]; } return; } //一层一层的求,我们就可以建好一个初步的树啦
然后是修改(change)
#define ls 2*rt,l,(l+r)/2 //左右儿子,和之前一样 #define rs 2*rt+1,(l+r)/2+1,r #define ll long long void change(ll rt,ll l,ll r,ll L,ll R,ll add) //当前点,当前区间的左右端点,需要修改的区间的左右端点,需要给每个基本点加上的值 { if(l>=L&&r<=R)//如果说当前区间是需要修改区间的子集 { su[rt]+=add*(r-l+1); //那么就修改当前点,注意乘上当前区间长度 o[rt]+=add;
//记得修改懒标记 return;//别忘了返回! } if(o[rt]!=0) //如果说我们恰好经过了一个被打上懒标记的点,那不如就顺手把它的懒标记下传好了 { //修改左右儿子的值 su[rt*2]+=o[rt]*((r+l)/2-l+1);// (r+l)/2是区间中点 su[rt*2+1]+=o[rt]*(r-(r+l)/2);//实际应乘以(r-((r+l)/2+1)+1)但+1-1抵消了 o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; //下传懒标记注意是加上父节点的懒标记不是等于 o[rt]=0;//清除懒标记 } if(L<=(l+r)/2) //二分思想,如果需要修改的区间左端点在当前区间中点的左边,即当前区间中点左侧有需要修改的点的话 { change(ls,L,R,add);//那就去修改啊 } if(R>(l+r)/2)//同理 { change(rs,L,R,add); } su[rt]=su[2*rt]+su[2*rt+1];//橘氏春秋有云(什么鬼):有下就有上,改完记得上传 return; }
呼啊,已经完成2/3了,坚持就是胜利!↖(^ω^)↗
查询(find)
void find(ll rt,ll l,ll r,ll L,ll R) //当前点,当前区间左右端点,需要查询的区间左右端点 { if(l>=L&&r<=R)//如果当前区间是查询区间的子集 { ans[c]+=su[rt];//答案就加上当前点的值 } else//不然就找找它应该在那个区间里面 { if(o[rt]!=0)//顺便下传rt的懒标记 { su[rt*2]+=o[rt]*((r+l)/2-l+1); su[rt*2+1]+=o[rt]*(r-(r+l)/2); o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; o[rt]=0; } if(L<=(l+r)/2)//二分思想,如果左边有点 { find(ls,L,R);//那就找找左边 } if(R>(l+r)/2)//如果右边有点 { find(rs,L,R);//那就找找右边 } su[rt]=su[2*rt]+su[2*rt+1];//还是那句老话,橘氏春秋有云:有下就有上 } return;//看到return我就开心↖(^ω^)↗ }
哇吼,结束了才怪,接下来是总代码!
//线段树要写成lazy[i]+=lazy[祖先]的形式 //温馨提示,炒鸡重要,我这个蒟蒻就被坑了嘤嘤嘤 #include<iostream> #include<cstdio> #define ls 2*rt,l,(l+r)/2 #define rs 2*rt+1,(l+r)/2+1,r #define ll long long using namespace std; int n,m,a,c; ll su[400005],x,y,k,ans[100005],o[400005];//数组开4倍 void build(ll rt,ll l,ll r) { if(r==l) { scanf("%lld",&su[rt]); } else { build(ls); build(rs); su[rt]=su[2*rt]+su[2*rt+1]; } return; } void change(ll rt,ll l,ll r,ll L,ll R,ll add) { if(l>=L&&r<=R) { su[rt]+=add*(r-l+1); o[rt]+=add; return; } if(o[rt]!=0) { su[rt*2]+=o[rt]*((r+l)/2-l+1); su[rt*2+1]+=o[rt]*(r-(r+l)/2); o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; o[rt]=0; } if(L<=(l+r)/2) { change(ls,L,R,add); } if(R>(l+r)/2) { change(rs,L,R,add); } su[rt]=su[2*rt]+su[2*rt+1]; return; } void find(ll rt,ll l,ll r,ll L,ll R) { if(l>=L&&r<=R) { ans[c]+=su[rt]; } else { if(o[rt]!=0) { su[rt*2]+=o[rt]*((r+l)/2-l+1); su[rt*2+1]+=o[rt]*(r-(r+l)/2); o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; o[rt]=0; } if(L<=(l+r)/2) { find(ls,L,R); } if(R>(l+r)/2) { find(rs,L,R); } su[rt]=su[2*rt]+su[2*rt+1]; } return; } int main() { scanf("%d %d",&n,&m);//n个基本点,m次操作 build(1,1,n); for(int i=1;i<=m;i++) { scanf("%d",&a); if(a==1)//我们要进行区间加啦 { scanf("%lld %lld %lld",&x,&y,&k);//在x到y上加k change(1,1,n,x,y,k); // for(int i=1;i<=2*n;i++)cout<<" "<<i<<"="<<su[i]; // cout<<"\n"; // 写给需要调试的小可爱的 } if(a==2)//查询 { c++;//个人喜欢统一输出,c记录第几次询问 scanf("%lld %lld",&x,&y);//查询x到y的和 find(1,1,n,x,y); } } for(int i=1;i<=c;i++) { printf("%lld\n",ans[i]);//统一输出答案 } }
这样,一棵完完整整的基础简化版的线段树就写完了
如果你看完上面的觉得很简单,那你可以继续学习接下来的zkw线段树了
但是如果你觉得没那么简单,一定去练几个题再回来看下面的
zkw线段树不知道比递归线段树快到哪里去了,跑得嗷嗷的
看不懂就画图,手模
n是数组大小
单点修改 区间求和
#include<iostream> #include<cstdio> using namespace std; int n,m,q,ans,l,r; int t[300000]; char q1[3]; void build()//非递归建树,从m+1开始,多余的空间我不要了(任性) { for(m=1;m<=n+1;m<<=1); for(int i=m+1;i<=m+n;i++) scanf("%d",&t[i]); for(int i=m-1;i>=1;i--) t[i]=t[i<<1]+t[i<<1|1]; } void change(int x,int a)//这个不能再短 { for(x+=m;x;x>>=1) t[x]+=a; } void ask(int l,int r) { for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1) { if(~l&1)ans+=t[l^1]; if(r&1) ans+=t[r^1]; } printf("%d\n",ans); } int main()//按需填写 { ... }
区间修改 区间求和
#include<iostream> #include<cstdio> using namespace std; void build()//建树一样的 { for(m=1;m<=n+1;m<<=1); for(int i=m+1;i<=m+n;i++) scanf("%d",&t[i]); for(int i=m-1;i>=1;i--) t[i]=t[i<<1]+t[i<<1|1]; } void change(int l,int r,int k)//标记不下传,永久化 { int ln=0;//左指针走了多少了 int rn=0;//右指针走了多少了 int nn=1;//这层的点的子树多大 for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1,nn<<=1)//这里是开区间 { t[l]+=k*ln; t[r]+=k*rn; if(~l&1)//左指针是左儿子,兄弟该被修改 { add[l^1]+=k; t[l^1]+=k*nn; ln+=nn; } if(r&1)//右指针是右儿子,同理 { add[r^1]+=k; t[r^1]+=k*nn; rn+=nn; } } for(;l;l>>=1,r>>=1)//加到底 { t[l]+=k*ln; t[r]+=k*rn; } } void ask(int l,int r) { int ln=0; int rn=0; int nn=1; int ans=0; for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1,nn<<=1)//注意nn { if(add[l]) ans+=add[l]*ln; if(add[r]) ans+=add[r]*rn; if(~l&1) { ans+=t[l^1]; ln+=nn; } if(r&1) { ans+=t[r^1]; rn+=nn; } } for(;l;l>>=1,r>>=1)//加到底 { ans+=add[l]*ln; ans+=add[r]*rn; } } int main() { ... }
区间修改 区间最值
#include<iostream> #include<cstdio> using namespace std; int l,r,n,q,m,ans,k,a; int t[100000]; void build() { for(m=1;m<=n+1;m<<=1); for(int i=m+1;i<=m+n;i++) scanf("%d",&t[i]); for(int i=m-1;i>=1;i--)//区间最值有优化,建树和区间求和不一样 { t[i]=min(t[i<<1],t[i<<1|1]);//类似差分 t[i<<1]-=t[i]; t[i<<1|1]-=t[i]; } } void change(int l,int r,int k) { int tmp; for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1) { if(~l&1)t[l^1]+=k; if(r&1) t[r^1]+=k; tmp=min(t[l],t[l^1]);//继续差分 t[l]-=tmp; t[l^1]-=tmp; t[l>>1]+=tmp; tmp=min(t[r],t[r^1]); t[r]-=tmp; t[r^1]-=tmp; t[r>>1]+=tmp; } for(;l!=1;l>>=1)//差分到底 { tmp=min(t[l],t[l^1]); t[l]-=tmp; t[l^1]-=tmp; t[l>>1]+=tmp; } } void ask(int l,int r) { lans=0; rans=0; if(l!=r) { for(l+=m,r+=m;l^r^1;l>>=1,r>>=1) { lans+=t[l]; rans+=t[r]; if(~l&1)lans=min(t[l^1],lans); if(r&1) rans=min(t[r^1],rans); } } ans=min(lans+t[l],rans+t[r]); while(s>1) ans+=t[s>>=1];//一定要到底 printf("%d\n",ans); } int main() { ... }
有问题的话可以问呦~虽然我也不一定会但是我会尽力解答的!
感谢阅读,求赞👍QwQ


 浙公网安备 33010602011771号
浙公网安备 33010602011771号