ROC与AUC原理

做梦当财神

随笔- 168 文章- 0 评论- 16

ROC与AUC原理

来自：https://blog.csdn.net/shenxiaoming77/article/details/72627882

来自：https://blog.csdn.net/u010705209/article/details/53037481

在分类模型中，roc曲线和auc曲线作为衡量一个模型拟合程度的指标。

分类模型评估：

指标	描述	Scikit-learn函数
Precision	AUC	from sklearn.metrics import precision_score
Recall	召回率	from sklearn.metrics import recall_score
F1	F1值	from sklearn.metrics import f1_score
Confusion Matrix	混淆矩阵	from sklearn.metrics import confusion_matrix
ROC	ROC曲线	from sklearn.metrics import confusion_matrix
AUC	ROC曲线下的面积	from sklearn.metrics import auc

回归模型评估：

指标	描述	Scikit-learn函数
Mean Square Error (MSE, RMSE)	平均方差	from sklearn.metrics import mean_squared_error
Absolute Error (MAE, RAE)	绝对误差	from sklearn.metrics import mean_absolute_error, median_absolute_error
R-Squared	R平方值	from sklearn.metrics import r2_score

roc和auc定义

roc全称是“受试者工作特征”（recevier operating characteristic）。roc曲线的面积就是auc（area under the curve）。auc用于衡量“二分类问题”机器学习算法性能（泛化能力）。

1. 了解roc首先了解混淆矩阵：

例如用一个分类模型来判别一个水果是苹果还是梨，混淆矩阵将会模型的预测结果总结成如下表所示的表格。

		模型预测结果	模型预测结果
		苹果	梨
真是结果	苹果	10	2
真是结果	梨	3	15

通过上述表格可以看出，样本的数量一共是 $10 + 2 + 3 + 15 = 30$

混淆矩阵

对于一个二分类的模型，其模型的混淆矩阵是一个 $2 \times 2$

		Predicted condition	Predicted condition
		positive	negative
True condition	positive	True Positive	True Negative
True condition	negative	False Positive	False Negative

混淆矩阵比模型的精度的评价指标更能够详细地反映出模型的”好坏”。模型的精度指标，在正负样本数量不均衡的情况下，会出现容易误导的结果

True Positive：真正类（TP），样本的真实类别是正类，并且模型预测的结果也是正类。
False Negative：假负类（FN），样本的真实类别是正类，但模型将其预测成为负类。
False Positive：假正类（FP），样本的真实类别是负类，但模型将其预测成正类。
True Negative：真负类（TN），样本的真实类别是负类，并且模型将其预测成为负类。

混淆矩阵中，衍生出各种评价的指标。

精度：

模型预测正确的个数 / 样本的总个数，

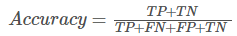
一般情况下，模型的精度越高，说明模型的效果越好。

召回率：

模型预测为正类的样本的数量，占总的正类样本数量的比值。

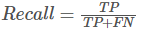
Recall越高，说明有更多的正类样本被模型预测正确，模型的效果越好。

TPR：

样本中的真实正例类别总数即TP+FN。TPR即True Positive Rate，TPR = TP/(TP+FN)。

FPR：
同理，样本中的真实反例类别总数为FP+TN。FPR即False Positive Rate，FPR=FP/(TN+FP)。

截断点：

还有一个概念叫”截断点”。机器学习算法对test样本进行预测后，可以输出各test样本对某个类别的相似度概率。比如t1是P类别的概率为0.3，一般我们认为概率低于0.5，t1就属于类别N。这里的0.5，就是”截断点”。
总结一下，对于计算ROC，最重要的三个概念就是TPR, FPR, 截断点。

截断点取不同的值，TPR和FPR的计算结果也不同。将截断点不同取值下对应的TPR和FPR结果画于二维坐标系中得到的曲线，就是ROC曲线。横轴用FPR表示。

2. sklearn计算roc

sklearn给出了一个计算roc的例子：

y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)

通过计算，得到的结果（TPR, FPR, 截断点）为

fpr = array([ 0. ,  0.5,  0.5,  1. ])
tpr = array([ 0.5,  0.5,  1. ,  1. ])
thresholds = array([ 0.8 ,  0.4 ,  0.35,  0.1 ])    #截断点

将结果中的FPR与TPR画到二维坐标中，得到的ROC曲线如下（蓝色线条表示），ROC曲线的面积用AUC表示（淡黄色阴影部分）。

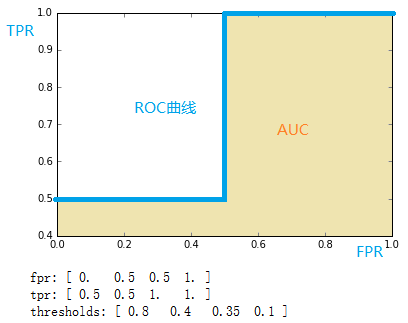
详细计算过程：

y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])

(1). 分析数据

y是一个一维数组（样本的真实分类）。数组值表示类别（一共有两类，1和2）。我们假设y中的1表示反例，2表示正例。即将y重写为：

y_true = [0, 0, 1, 1]

score即各个样本属于正例的概率。

(2). 针对score，将数据排序

样本	预测属于P的概率(score)	真实类别
y[0]	0.1	N
y[2]	0.35	P
y[1]	0.4	N
y[3]	0.8	P

(3). 将截断点依次取值为score值

将截断点依次取值为0.1, 0.35, 0.4, 0.8时，计算TPR和FPR的结果。

3.1. 截断点为.01

说明只要score>=0.1，它的预测类别就是正例。
此时，因为4个样本的score都大于等于0.1，所以，所有样本的预测类别都为P。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [1, 1, 1, 1]

TPR = TP/(TP+FN) = 1
FPR = FP/(TN+FP) = 1

3.2. 截断点为0.35

说明只要score>=0.35，它的预测类别就是P。
此时，因为4个样本的score有3个大于等于0.35。所以，所有样本的预测类有3个为P（2个预测正确，1一个预测错误）；1个样本被预测为N（预测正确）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 1, 1, 1]

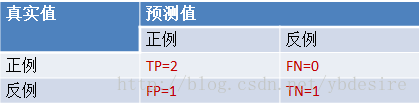
TPR = TP/(TP+FN) = 1
FPR = FP/(TN+FP) = 0.5

3.3. 截断点为0.4

说明只要score>=0.4，它的预测类别就是P。
此时，因为4个样本的score有2个大于等于0.4。所以，所有样本的预测类有2个为P（1个预测正确，1一个预测错误）；2个样本被预测为N（1个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 1, 0, 1]

TPR = TP/(TP+FN) = 0.5
FPR = FP/(TN+FP) = 0.5

3.4. 截断点为0.8

说明只要score>=0.8，它的预测类别就是P。所以，所有样本的预测类有1个为P（1个预测正确）；3个样本被预测为N（2个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 0, 0, 1]

TPR = TP/(TP+FN) = 0.5
FPR = FP/(TN+FP) = 0

(4). 心得

用下面描述表示TPR和FPR的计算过程，更容易记住

TPR：真实的正例中，被预测正确的比例
FPR：真实的反例中，被预测正确的比例

posted @ 2020-06-30 11:10 xiaojikuaipao 阅读(302) 评论(0) 编辑收藏举报

刷新页面返回顶部

BioMarkerInfo

生物信息技术

ROC与AUC原理

做梦当财神

ROC与AUC原理

公告