KMeans 算法的实现

首先，KMeans是什么呢？

KMeans算法是聚类(cluster)算法中的一种非常经典的算法

KMeans的具体实现过程

1. 导入数据集，并设置簇的个数!
2. 随机设置聚类中心 \(C_i = {C_1, C_2 ... C_n}\)
3. 遍历所有的样本，并分别计算样本到每一个聚类中心的距离，将样本距中心距离最小的样本加入到相应的聚类中心
4. 遍历完所有的样本点后 计算每个簇的平均值作为新的聚类中心 并进行下一次迭代(即重复做第三步和第四步)
5. 在所有的样本点都无法更新后结束迭代 得到结果就是聚类的结果

算法过程

算法第三步 遍历样本 并且计算到簇的距离

# 遍历每一个样本点 并且找到最小的距离的簇 将样本放入该簇中
def find_closest_centroids(X, centroids):
    # K = centroids.shape[0]
    idx = np.zeros(X.shape[0], dtype=int)
    n = X.shape[0]
    for i in range(n):
        distance = []
        for j in range(centroids.shape[0]):
            distance.append(np.linalg.norm(X[i] - centroids[j]) ** 2)  # 使用欧氏距离计算距离
        idx[i] = np.argmin(distance) # 获取最近的簇的下标
    return idx

计算中心点的位置

# 更新簇的中心点进行迭代
def compute_centroids(X, idx, K):
    m, n = X.shape
    centorids = np.zeros((K, n))

    for k in range(K):
        points = X[idx == k]
        centorids[k] = np.mean(points, axis=0)
    return centorids

KMeans算法

def run_kMeans(X, initial_centroids, max_iters=10, plot_progress=False):
    """
    Runs the K-Means algorithm on data matrix X, where each row of X
    is a single example
    """
    # Initialize values
    m, n = X.shape
    K = initial_centroids.shape[0]
    centroids = initial_centroids
    previous_centroids = centroids
    idx = np.zeros(m)

    # Run K-Means
    for i in range(max_iters):

        # Output progress
        print("K-Means iteration %d/%d" % (i, max_iters - 1))

        # For each example in X, assign it to the closest centroid
        idx = find_closest_centroids(X, centroids) # 计算距离 并进行分类

        # Optionally plot progress
        if plot_progress:
            plot_progress_kMeans(X, centroids, previous_centroids, idx, K, i)
            previous_centroids = centroids

        # Given the memberships, compute new centroids
        centroids = compute_centroids(X, idx, K) # 更新中心点
    plt.show()
    return centroids, idx

# main
X = load_data()
print(X)
# Set initial centroids
initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])
K = 3

# Number of iterations
max_iters = 10

centroids, idx = run_kMeans(X, initial_centroids, max_iters, plot_progress=True)

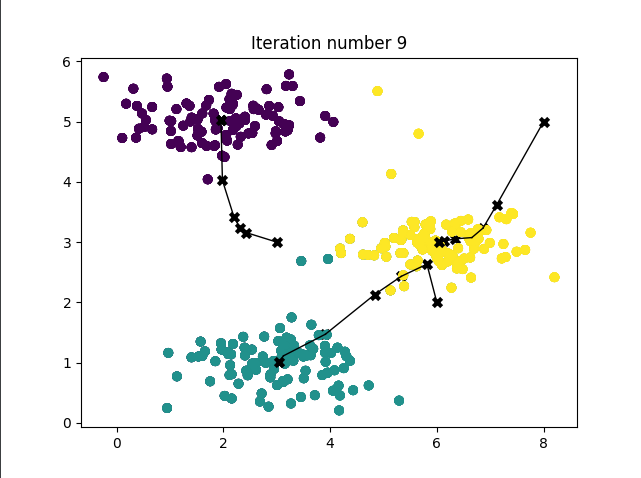
                                       结果如图所示