4-9 风格代价函数

风格代价函数（Style cost function）

比如你有这样一张图片，现在你选择了某一层l，比如这一层去为图片的风格定义一个深度测量，现在我们要做的就是将图片的风格定义为l层中各个通道之间激活项的相关系数。

现在你将l层的激活项取出，这是个${n_H} \times {n_W} \times {n_C}$的激活项，它是一个三维的数据块。

我把它的不同通道渲染成不同的颜色。在这个例子中，假如我们有 5 个通道为了方便讲解，我将它们染成了五种颜色。一般情况下，我们在神经网络中会有许多通道，但这里只用 5 个通道，会更方便我们理解：

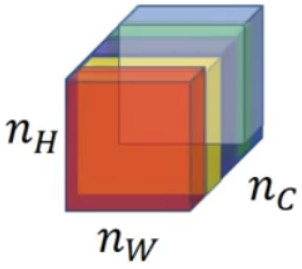
为了能捕捉图片的风格，你需要进行下面这些操作，首先，先看前两个通道，前两个通道分别是图中的红色和黄色部分，那我们该如何计算这两个通道间激活项的相关系数呢？

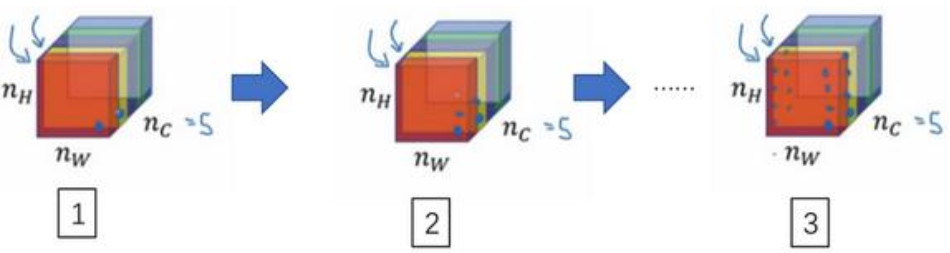
第一个通道中含有某个激活项，第二个通道也含有某个激活项，于是它们组成了一对数字（编号 1 所示）。然后我们再看看这个激活项块中其他位置的激活项，它们也分别组成了很多对数字（编号 2， 3 所示），分别来自第一个通道，也就是红色通道和第二个通道，也就是黄色通道。现在我们得到了很多个数字对，当我们取得这两个${n_H} \times {n_W}$的通道中所有的数字对后，现在该如何计算它们的相关系数呢？它是如何决定图片风格的呢？

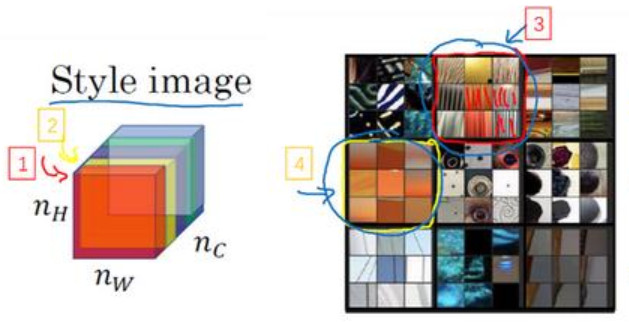
这个红色的通道（编号 1）对应的是这个神经元，它能找出图片中的特定位置是否含有这些垂直的纹理（编号 3），而第二个通道也就是黄色的通道（编号 2），对应这个神经元（编号 4），它可以粗略地找出橙色的区域。什么时候两个通道拥有高度相关性呢？如果它们有高度相关性，那么这幅图片中出现垂直纹理的地方（编号 2），那么这块地方（编号 4）很大概率是橙色的。如果说它们是不相关的，又是什么意思呢？显然，这意味着图片中有垂直纹理的地方很大概率不是橙色的。而相关系数描述的就是当图片某处出现这种垂直纹理时，该处又同时是橙色的可能性。

相关系数这个概念为你提供了一种去测量这些不同的特征的方法，比如这些垂直纹理，这些橙色或是其他的特征去测量它们在图片中的各个位置同时出现或不同时出现的频率。

如果我们在通道之间使用相关系数来描述通道的风格，你能做的就是测量你的生成图像中第一个通道（编号 1）是否与第二个通道（编号 2）相关，通过测量，你能得知在生成的图像中垂直纹理和橙色同时出现或者不同时出现的频率，这样你将能够测量生成的图像的风格与输入的风格图像的相似程度。

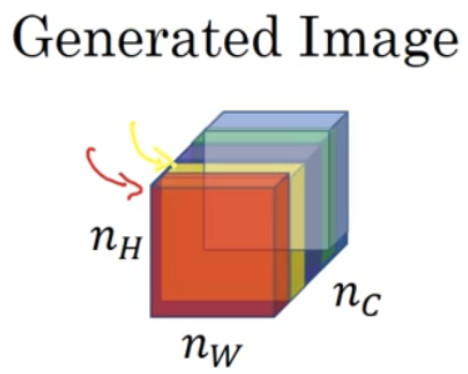
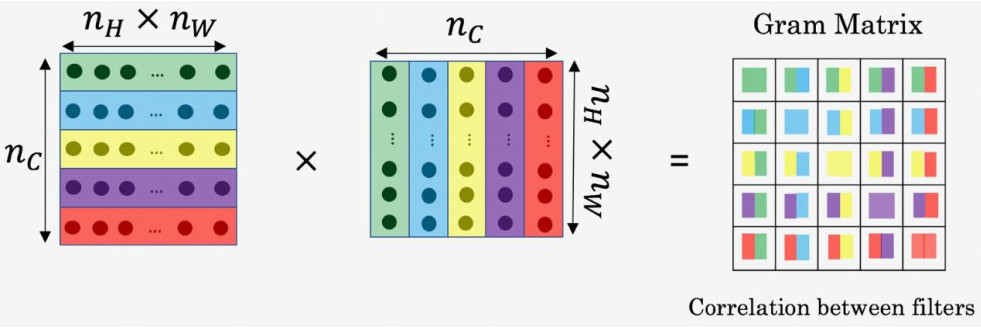
对于这两个图像，也就是风格图像与生成图像，你需要计算一个风格矩阵，说得更具体一点就是用l层来测量风格。

$Leta_{i,j,k}^{[l]} = activation\;at(i,j,k).{G^{[l](s)}}\;is\;n_c^{[l]} \times n_c^{[l]}$

假设$a_{i,j,k}^{[l]}$ 为隐藏层l中$(i,j,k)$ 位置的激活项， i， j， k分别代表该位置的高度、宽度以及对应的通道数。现在你要做的就是去计算一个关于l层和风格图像的矩阵，即${G^{[l](s)}}$, （l表示层数， S表示风格图像），这${G^{[l](s)}}$ 是一个${n_c} \times {n_c}$的矩阵，同样地，我们也对生成的图像进行这个操作。

但是现在我们先来定义风格图像，设这个关于l层和风格图像的， G是一个矩阵，这个矩阵的高度和宽度都是l层的通道数。在这个矩阵中k和k′元素被用来描述k通道和k′通道之间的相关系数。具体地：

$G_{kk'}^{^{[l](s)}} = \sum\limits_{i = 1}^{n_H^{[l]}} {\sum\limits_{j = 1}^{n_W^{[l]}} {a_{i,j,k}^{[l][{\rm{S}}]}a_{i,j,k'}^{[l][{\rm{S}}]}} }$

用符号i， j表示下界，对i， j， k位置的激活项$a_{i,j,k}^{[l]}$ ，乘以同样位置的激活项，也就是i,j,k′位置的激活项，即$a_{i,j,k'}^{[l]}$ ，将它们两个相乘。然后i和j分别加到 l 层的高度和宽度，即$n_H^{[l]}$ 和$n_W^{[l]}$ ，将这些不同位置的激活项都加起来。$(i,j,k)$ 和$(i,j,k')$ 中x坐标和y坐标分别对应高度和宽度，将k通道和k′通道上这些位置的激活项都进行相乘。我一直以来用的这个公式，严格来说，它是一种非标准的互相关函数，因为我们没有减去平均数，而是将它们直接相乘。

这就是输入的风格图像所构成的风格矩阵，然后，我们再对生成图像做同样的操作。

$G_{kk'}^{^{[l](G)}} = \sum\limits_{i = 1}^{n_H^{[l]}} {\sum\limits_{j = 1}^{n_W^{[l]}} {a_{i,j,k}^{[l][G]}a_{i,j,k'}^{[l][G]}} }$

${a_{i,j,k}^{[l][S]}}$ 和${a_{i,j,k}^{[l][G]}}$ 中的上标(S)和(G)分别表示在风格图像 S 中的激活项和在生成图像G的激活项。我们之所以用大写字母S来代表这些风格矩阵，是因为在线性代数中这种矩阵有时也叫 Gram 矩阵，但在这里我只把它们叫做风格矩阵。

所以你要做的就是计算出这张图像的风格矩阵，以便能够测量出刚才所说的这些相关系数。更正规地来表示，我们用$a_{i,j,k}^{[l]}$来记录相应位置的激活项，也就是l层中的i, j, k位置，所以i代表高度， j代表宽度， k代表着l中的不同通道。之前说过，我们有 5 个通道，所以k就代表这五个不同的通道。

对于这个风格矩阵，你要做的就是计算这个矩阵也就是${G^{[l]}}$ 矩阵，它是个${n_c} \times {n_c}$的矩阵，也就是一个方阵。记住，因为这里有${n_c}$个通道，所以矩阵的大小是${n_c} \times {n_c}$。以便计算每一对激活项的相关系数，所以$G_{kk'}^{^{[l]}}$ 可以用来测量k通道与k′通道中的激活项之间的相关系数， k和k′会在 1 到${n_c}$之间取值， ${n_c}$就是l层中通道的总数量。

当在计算${G^{[l]}}$ 下标kk′只代表一种元素，和之前一样i，j从一开始往上加，对应$(i,j,k)$位置的激活项与对应$(i,j,k')$位置的激活项相乘。

这个i和j是激活块中对应位置的坐标，也就是该激活项所在的高和宽，所以i会从 1 加到$n_H^{[l]}$ ， j会从 1 加到$n_W^{[l]}$, ， k和k′则表示对应的通道，所以k和k′值的范围是从1 开始到这个神经网络中该层的通道数量$n_{\rm{C}}^{^{[l]}}$, 这个式子就是把图中各个高度和宽度的激活项都遍历一遍，并将k和k′通道中对应位置的激活项都进行相乘，这就是$G_{kk'}^{^{[l]}}$ 的定义。通过对k和k′通道中所有的数值进行计算就得到了G矩阵，也就是风格矩阵。

$G_{kk'}^{^{[l]}} = \sum\limits_{i = 1}^{n_H^{[l]}} {\sum\limits_{j = 1}^{n_W^{[l]}} {a_{i,j,k}^{[l]}a_{i,j,k'}^{[l]}} }$

要注意，如果两个通道中的激活项数值都很大，那么$G_{kk'}^{^{[l]}}$ 也会变得很大，对应地，如果他们不相关那么$G_{kk'}^{^{[l]}}$ 就会很小。严格来讲，我一直使用这个公式来表达直觉想法，但它其实是一种非标准的互协方差，因为我们并没有减去均值而只是把这些元素直接相乘，这就是计算图像风格的方法。

$G_{kk'}^{^{[l](s)}} = \sum\limits_{i = 1}^{n_H^{[l]}} {\sum\limits_{j = 1}^{n_W^{[l]}} {a_{i,j,k}^{[l][{\rm{S}}]}a_{i,j,k'}^{[l][{\rm{S}}]}} }$

你要同时对风格图像S和生成图像G都进行这个运算，为了区分它们，我们在它的右上角加一个(S)，表明它是风格图像S，这些都是风格图像 S 中的激活项，之后你需要对生成图像也做相同的运算。

$G_{kk'}^{^{[l](G)}} = \sum\limits_{i = 1}^{n_H^{[l]}} {\sum\limits_{j = 1}^{n_W^{[l]}} {a_{i,j,k}^{[l][G]}a_{i,j,k'}^{[l][G]}} }$

和之前一样，再把公式都写一遍，把这些都加起来，为了区分它是生成图像，在这里放一个(G)。

现在，我们有 2 个矩阵，分别从风格图像S和生成图像G。

再提醒一下，我们一直使用大写字母G来表示矩阵，是因为在线性代数中，这种矩阵被称为 Gram 矩阵，但在本视频中我把它叫做风格矩阵，我们取了 Gram 矩阵的首字母G来表示这些风格矩阵。（过程见下图）

最后，如果我们将S和G代入到风格代价函数中去计算，这将得到这两个矩阵之间的误差，因为它们是矩阵，所以在这里加一个F（Frobenius 范数，编号 1 所示），这实际上是计算两个矩阵对应元素相减的平方的和，我们把这个式子展开，从k和k′开始作它们的差，把

对应的式子写下来，然后把得到的结果都加起来，作者在这里使用了一个归一化常数，也就是$\frac{1}{{2n_{\rm{H}}^{^{[l]}}n_{\rm{W}}^{^{[l]}}n_{\rm{C}}^{^{[l]}}}}$ ，再在外面加一个平方，但是一般情况下你不用写这么多，一般我们只要将它乘以一个超参数$\beta$就行。

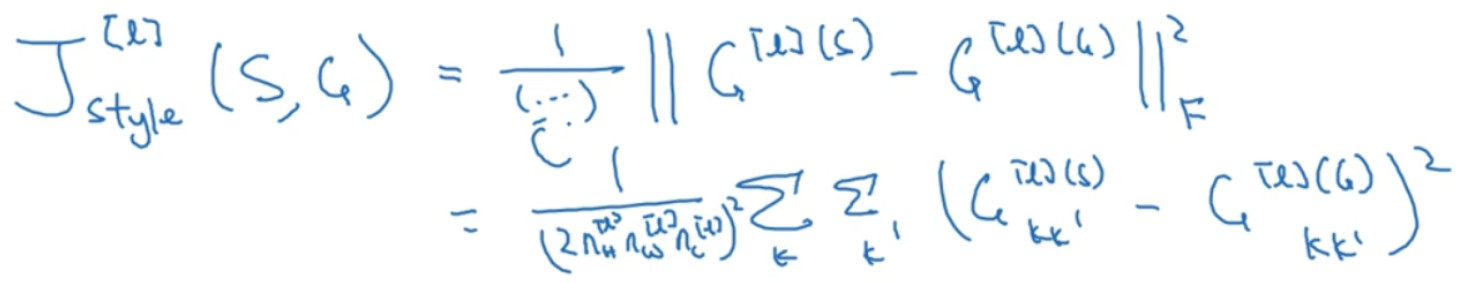
最后，这是对l层定义的风格代价函数，和之前你见到的一样，这是两个矩阵间一个基本的 Frobenius 范数，也就是S图像和G图像之间的范数再乘上一个归一化常数，不过这不是很重要。实际上，如果你对各层都使用风格代价函数，会让结果变得更好。如果要对各层都使用风格代价函数，你可以这么定义代价函数，把各个层的结果（各层的风格代价函数）都加起来，这样就能定义它们全体了。我们还需要对每个层定义权重，也就是一些额外的超参数，我们用${\lambda ^{[l]}}$ 来表示，这样将使你能够在神经网络中使用不同的层，包括之前的一些可以测量类似边缘这样的低级特征的层，以及之后的一些能测量高级特征的层，使得我们的神经网络在计算风格时能够同时考虑到这些低级和高级特征的相关系数。这样，在基础的训练中你在定义超参数时，可以尽可能的得到更合理的选择。为了把这些东西封装起来，你现在可以定义一个全体代价函数：

$J(G) = \alpha {J_{connect(C,G)}} + \beta {J_s}_{tyle}({\rm{S,G}})$

之后用梯度下降法，或者更复杂的优化算法来找到一个合适的图像G，并计算$J(G)$的最小值，这样的话，你将能够得到非常好看的结果，你将能够得到非常漂亮的结果。