4-3 Triplet 损失

Triplet 损失

要想通过学习神经网络的参数来得到优质的人脸图片编码，方法之一就是定义三元组损失函数然后应用梯度下降。

为了应用三元组损失函数，你需要比较成对的图像，比如这个图片，为了学习网络的参数，你需要同时看几幅图片，对于前两张图片，你想要它们的编码相似，因为这是同一个人，对于后两张图片，你会想要它们的编码差异大一些，因为这是不同的人。

用三元组损失的术语来说，你要做的通常是看一个 Anchor 图片，你想让 Anchor 图片和 Positive 图片（Positive 意味着是同一个人）的距离很接近。然而，当 Anchor 图片与 Negative图片（Negative 意味着是非同一个人）对比时，你会想让他们的距离离得更远一点。

这就是为什么叫做三元组损失，它代表你通常会同时看三张图片，你需要看 Anchor 图片、 Postive 图片，还有 Negative 图片，我要把 Anchor 图片、 Positive 图片和 Negative 图片简写成 A、P、N。

把这些写成公式的话，你想要的是网络的参数或者编码能够满足以下特性，也就是说你想要${\left\| {f(A) - f(P)} \right\|^2}$,你希望这个数值很小，准确地说，你想让它小于等${f(A)}$ 和${f(N)}$ 之间的距离，或者说是它们的范数的平方，即：${\left\| {f(A) - f(P)} \right\|^2} \le {\left\| {f(A) - f(N)} \right\|^2}$，${\left\| {f(A) - f(P)} \right\|^2}$就是$d(A,P)$，${\left\| {f(A) - f(N)} \right\|^2}$就是$d(A,N)$，你可以把d看作是距离(distance) 函数，这也是为什么我们把它命名为d。

现在我要对这个表达式做一些小的改变，有一种情况满足这个表达式，但是没有用处，就是把所有的东西都学成 0，如果f总是输出 0， 即$0 - 0 \le 0$,这就是 0 减去 0 还等于 0， 如果所有图像的f都是一个零向量，那么总能满足这个方程。所以为了确保网络对于所有的编码不会总是输出 0，也为了确保它不会把所有的编码都设成互相相等的。另一种方法能让网络得到这种没用的输出，就是如果每个图片的编码和其他图片一样，这种情况，你还是得到 0-0。

为了阻止网络出现这种情况，我们需要修改这个目标，也就是，这个不能是刚好小于等于 0，应该是比 0 还要小，所以这个应该小于一个−a值, 即:

${\left\| {f(A) - f(P)} \right\|^2} - {\left\| {f(A) - f(N)} \right\|^2} \le  - a$

这里的a是另一个超参数，这个就可以阻止网络输出无用的结果。按照惯例，我们可以修改为如下的形式：

${\left\| {f(A) - f(P)} \right\|^2} - {\left\| {f(A) - f(N)} \right\|^2} + a \le 0$

而不是把-a写在后面，它也叫做间隔(margin)。

举个例子，假如间隔设置成 0.2，如果在这个例子中，$d(A,P) = 0.5$，如果 Anchor 和Negative 图片的d，$d(A,P)$ 只大一点，比如说 0.51，条件就不能满足。虽然 0.51 也是大于0.5 的，但还是不够好，我们想要$d(A,P)$比$d(A,N)$ 大很多，你会想让这个值$d(A,N)$ 至少是 0.7 或者更高，或者为了使这个间隔，或者间距至少达到 0.2，你可以把这项调大或者这个调小，这样这个间隔a，超参数a 至少是 0.2，在$d(A,P)$和$d(A,N)$ 之间至少相差 0.2，这就是间隔参数a的作用。它拉大了 Anchor 和 Positive 图片对和 Anchor 与 Negative 图片对之间的差距。

之间至少相差 0.2，这就是间隔参数a的作用。它拉大了 Anchor 和 Positive 图片对和 Anchor 与 Negative 图片对之间的差距。

为了定义这个损失函数，我们取这个和 0 的最大值:

$L(A,P,N) = \max ({\left\| {f(A) - f(P)} \right\|^2} - {\left\| {f(A) - f(N)} \right\|^2} + a,0)$

这个max函数的作用就是，只要这个${\left\| {f(A) - f(P)} \right\|^2} - {\left\| {f(A) - f(N)} \right\|^2} + a \le 0$，那么损失函数就是 0。

另一方面如果这个${\left\| {f(A) - f(P)} \right\|^2} - {\left\| {f(A) - f(N)} \right\|^2} + a \le 0$，然后你取它们的最大值，这样你会得到一个正的损失值。通过最小化这个损失函数达到的效果就是使这部分:

${\left\| {f(A) - f(P)} \right\|^2} - {\left\| {f(A) - f(N)} \right\|^2} + a$

成为 0，或者小于等于 0。只要这个损失函数小于等于 0，网络不会关心它负值有多大。

这是一个三元组定义的损失，整个网络的代价函数应该是训练集中这些单个三元组损失的总和。假如你有一个 10000 个图片的训练集，里面是 1000 个不同的人的照片，你要做的就是取这 10000 个图片，然后生成这样的三元组，然后训练你的学习算法，对这种代价函数用梯度下降，这个代价函数就是定义在你数据集里的这样的三元组图片上。

注意，为了定义三元组的数据集你需要成对的A和P，即同一个人的成对的图片，为了训练你的系统你确实需要一个数据集，里面有同一个人的多个照片。这是为什么在这个例子中，我说假设你有 1000 个不同的人的 10000 张照片，也许是这 1000 个人平均每个人 10 张照片，组成了你整个数据集。如果你只有每个人一张照片，那么根本没法训练这个系统。当然，训练完这个系统之后，你可以应用到你的一次学习问题上，对于你的人脸识别系统，可能你只有想要识别的某个人的一张照片。但对于训练集，你需要确保有同一个人的多个图片，至少是你训练集里的一部分人，这样就有成对的 Anchor 和 Positive 图片了。

一个问题是如果你从训练集中，随机地选择A、 P和N，遵守A和P是同一个人，而A和N是不同的人这一原则。有个问题就是，如果随机的选择它们，那么这个约束条件$d(A,P) + a \le d(A,N)$, 很容易达到，因为随机选择的图片，A和N比A和P差别很大的概率很大。这样网络并不能从中学到什么。

所以为了构建一个数据集，你要做的就是尽可能选择难训练的三元组A、 P和N。具体而言，你想要所有的三元组都满足这个条件$d(A,P) + a \le d(A,N)$, 难训练的三元组就是，你的A、 P和N的选择使得$d(A,P)$ 很接近$d(A,N)$, 即$d(A,P) \approx d(A,N)$, 这样 你的学习算法会竭尽全力使右边这个式子$d(A,N)$变大, 或者使左边这个式子$d(A,P)$ 变小，这样左右两边至少有一个a的间隔。并且选择这样的三元组还可以增加你的学习算法的计算效率，如果随机的选择这些三元组，其中有太多会很简单，梯度算法不会有什么效果，因为网络总是很轻松就能得到正确的结果，只有选择难的三元组梯度下降法才能发挥作用，使得这两边离得尽可能远。

总结一下，训练这个三元组损失你需要取你的训练集，然后把它做成很多三元组:

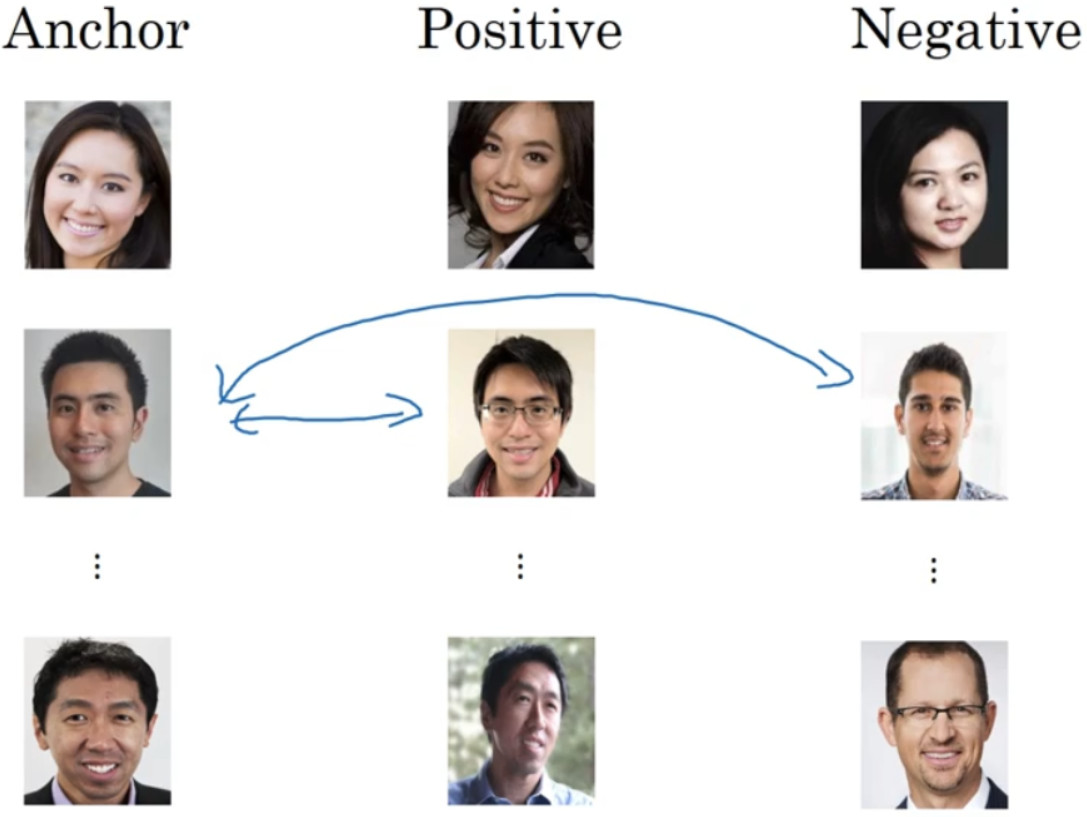
定义了这些包括A、 P和N图片的数据集之后，你还需要做的就是用梯度下降最小化我们之前定义的代价函数J，这样做的效果就是反向传播到网络中的所有参数来学习到一种编码，使得如果两个图片是同一个人，那么它们的d就会很小，如果两个图片不是同一个人，它们的d就会很大。