4-2 Siamese 网络

Siamese 网络（ Siamese network）

你经常看到这样的卷积网络，输入图片${x^{(1)}}$ ，然后通过一些列卷积，池化和全连接层，最终得到这样的特征向量，有时这个会被送进 softmax 单元来做分类，但是在这里不这样做，我们关注的是最终输出的向量，假设它是128维，它是由网络深层的全连接层计算出来的，给这 128 个数命个名字，把它叫做$f({x^{(1)}})$，你可以把$f({x^{(1)}})$ 看作是输入图像$f({x^{(1)}})$ 的编码。

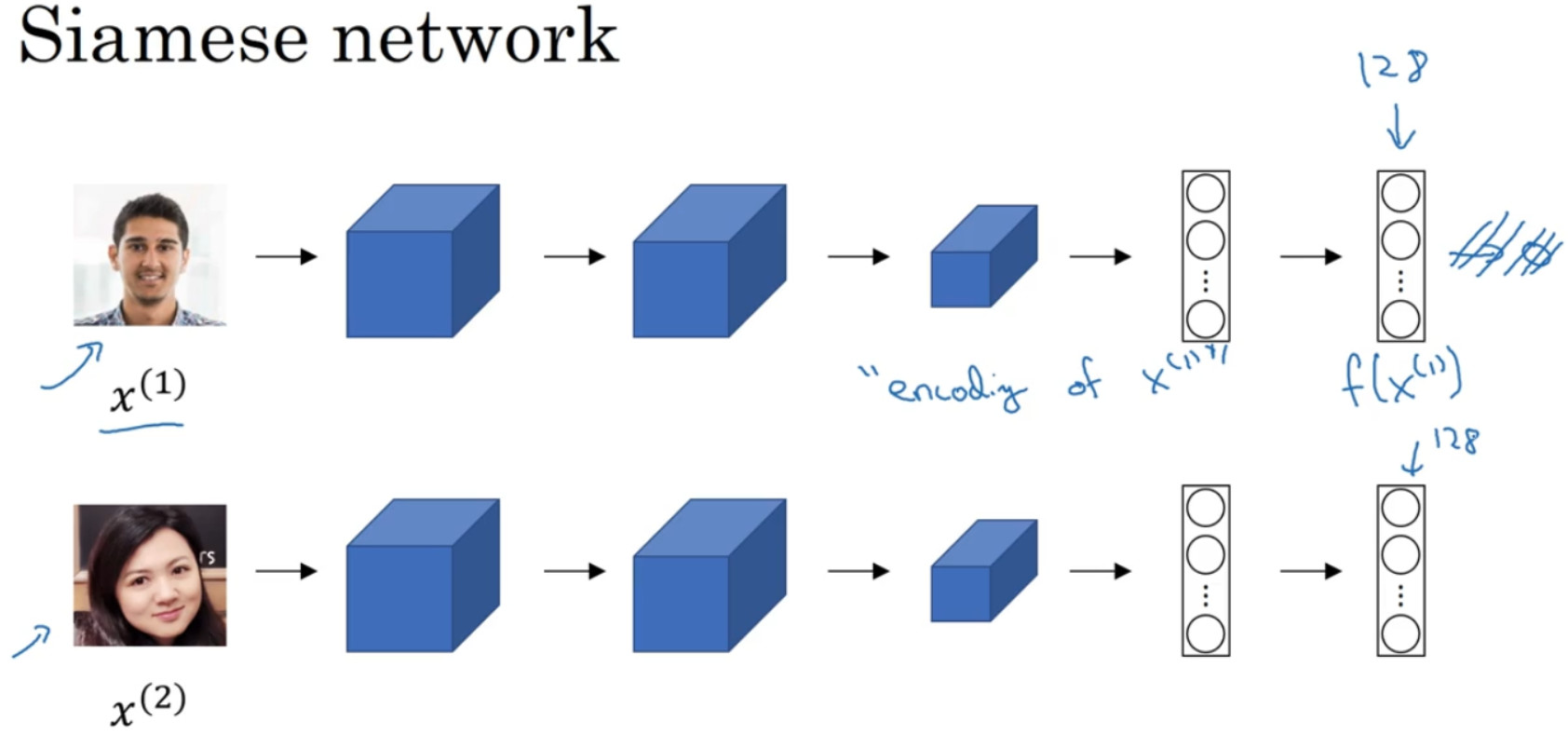
将$f({x^{(1)}})$，$f({x^{(2)}})$ 代表两个输入图片，喂给有同样参数的同样的神经网络，然后得到一个不同的 128 维的向量。最后如果你相信这些编码很好地代表了这两个图片，你要做的就是定义d，将$f({x^{(1)}})$，$f({x^{(2)}})$，的距离定义为这两幅图片的编码之差的范数，$d({x^{(1)}},{x^{(2)}}) = \left\| {f({x^{(1)}}) - f({x^{(2)}})} \right\|_2^2$。对于两个不同的输入，运行相同的卷积神经网络，然后比较它们，这一般叫做 Siamese网络架构。这个系统叫做 DeepFace。

神经网络的参数定义了一个编码函数$f({x^{(i)}})$，如果给定输入图像$f({x^{(i)}})$, 这个网络会输出$f({x^{(i)}})$ 的 128 维的编码。你要做的就是学习参数，使得如果两个图片$f({x^{(i)}})$, $f({x^{(j)}})$, 是同一个人，那么你得到的两个编码的距离就小。相反，如果$f({x^{(i)}})$, $f({x^{(j)}})$ 是不同的人，那么你会想让它们之间的编码距离大一点。

如果你改变这个网络所有层的参数，你会得到不同的编码结果，你要做的就是用反向传播来改变这些所有的参数，以确保满足这些条件。