3-1 目标定位

目标定位（ Object localization）

图片分类任务就是算法遍历图片，判断其中的对象是不是某个指定的类别，这就是图片分类。

定位分类问题。意味着我们不仅要用算法判断图片中是不是一辆汽车，还要在图片中标记出它的位置，用边框或红色方框把汽车圈起来。“定位”的意思是判断汽车在图片中的具体位置。

对于图片分类问题，例如，输入一张图片到多层卷积神经网络。这就是卷积神经网络，它会输出一个特征向量，并反馈给 softmax 单元来预测图片类型。

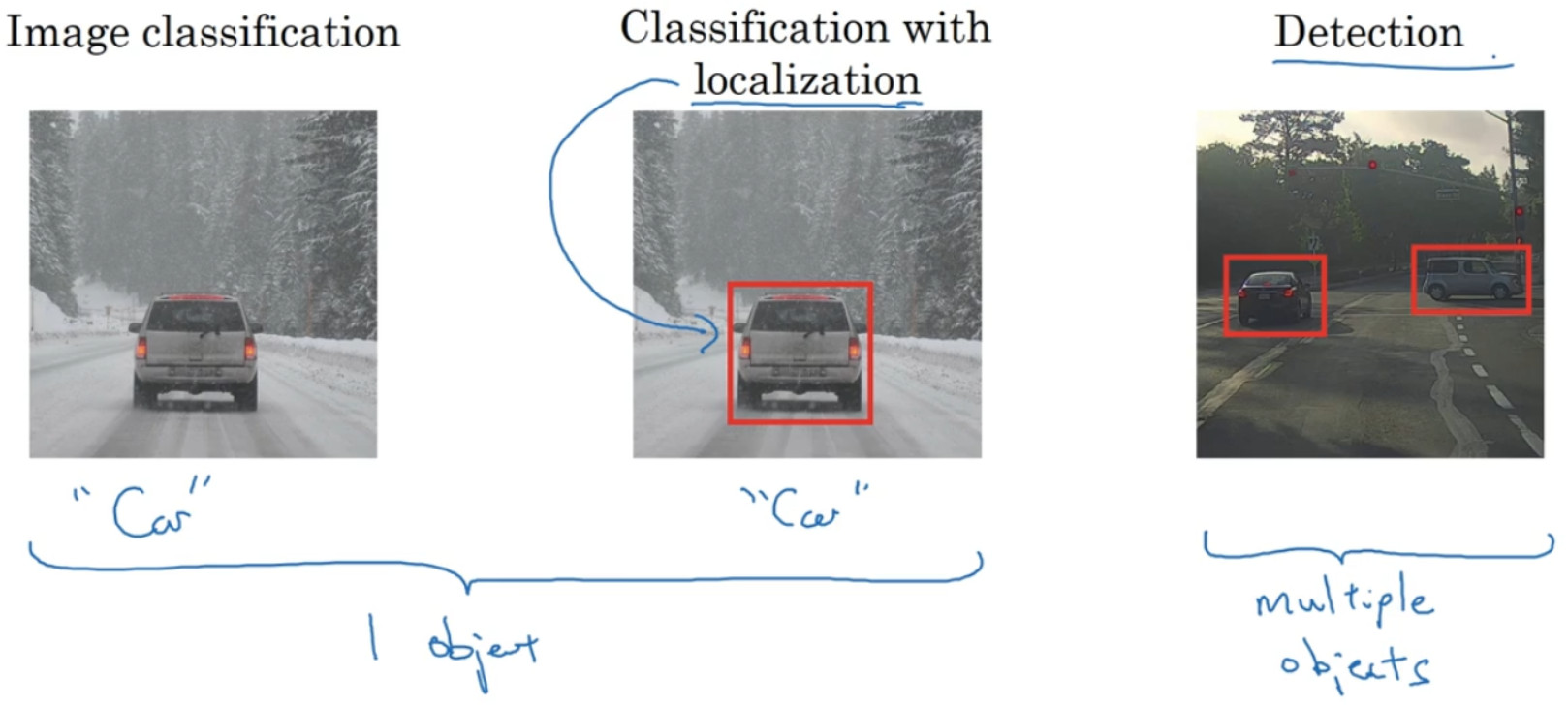
如果你正在构建汽车自动驾驶系统，那么对象可能包括以下几类：行人、汽车、摩托车和背景，这意味着图片中不含有前三种对象，也就是说图片中没有行人、汽车和摩托车，输出结果会是背景对象，这四个分类就是 softmax 函数可能输出的结果。

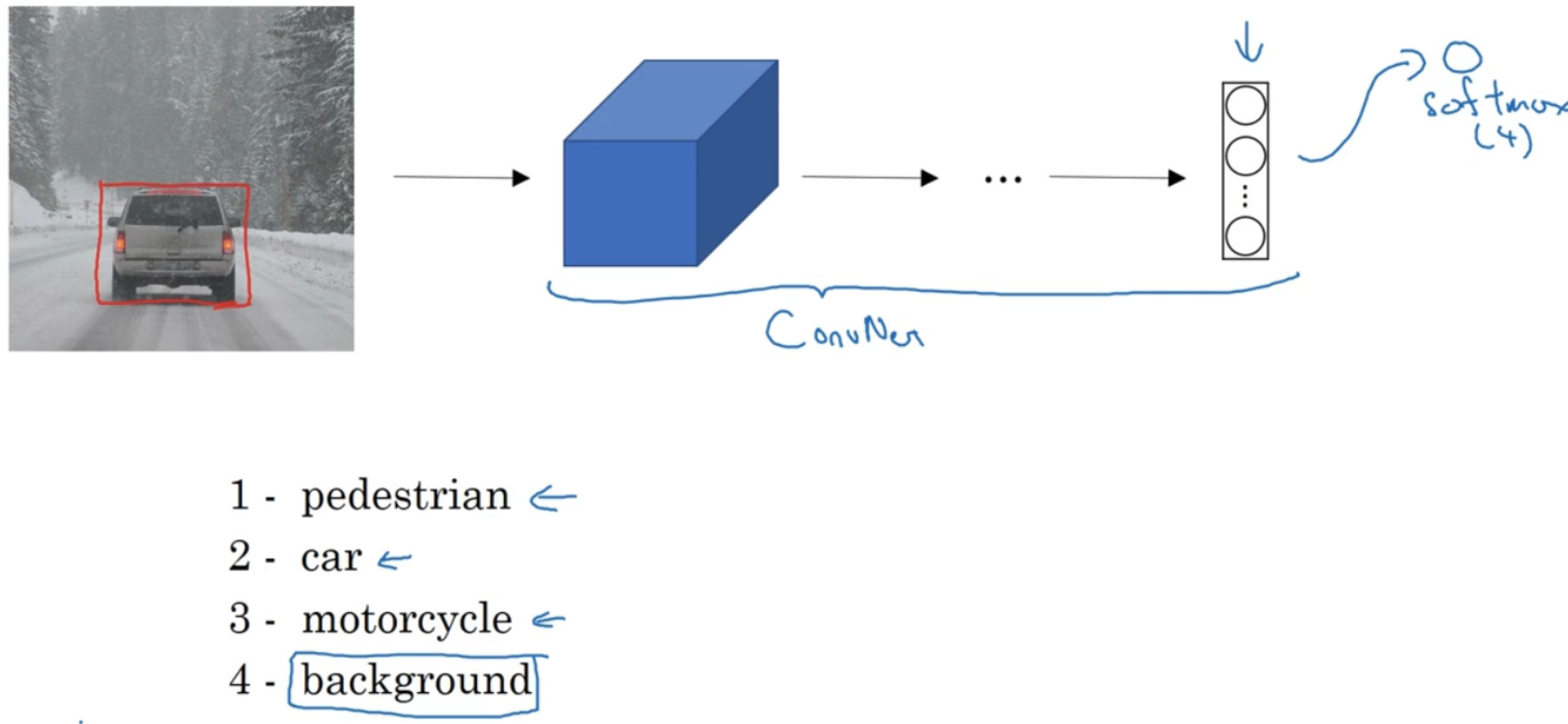
这就是标准的分类过程，如果你还想定位图片中汽车的位置，该怎么做呢？我们可以让神经网络多输出几个单元，输出一个边界框。具体说就是让神经网络再多输出 4 个数字，标记${b_x}$，${b_y}$ , ${b_w}$ , ${b_h}$ 这四个数字是被检测对象的边界框的参数化表示。

图片左上角的坐标为(0,0)，右下角标记为(1,1)。要确定边界框的具体位置，需要指定红色方框的中心点，这个点表示为$({b_x},{b_y})$,边界框的高度为${b_h}$,宽度为${b_w}$。因此训练集不仅包含神经网络要预测的对象分类标签，还要包含表示边界框的这四个数字，接着采用监督学习算法，输出一个分类标签，还有四个参数值，从而给出检测对象的边框位置。此例中, ${b_x}$的理想值是 0.5，${b_y}$大约是 0.7，${b_h}$约为 0.3，${b_w}$约为 0.4。

目标标签y的定义如下：

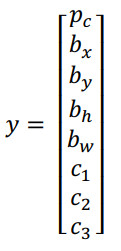
它是一个向量，第一个组件${p_c}$表示是否含有对象，如果对象属于前三类（行人、汽车、摩托车），则${p_c} = 1$，如果是背景，则图片中没有要检测的对象，则${p_c} = 0$，我们可以这样理解${p_c}$，它表示被检测对象属于某一分类的概率，背景分类除外。

如果检测到对象，就输出被检测对象的边界框参数${b_x}$，${b_y}$ , ${b_w}$ , ${b_h}$。最后，如果存在某个对象，那么${p_c} = 1$，同时输出${c_1}$，${c_2}$和${c_3}$，表示该对象属于 1-3 类中的哪一类，是行人，汽车还是摩托车。鉴于我们所要处理的问题，我们假设图片中只含有一个对象，所以针对这个分类定位问题，图片最多只会出现其中一个对象。

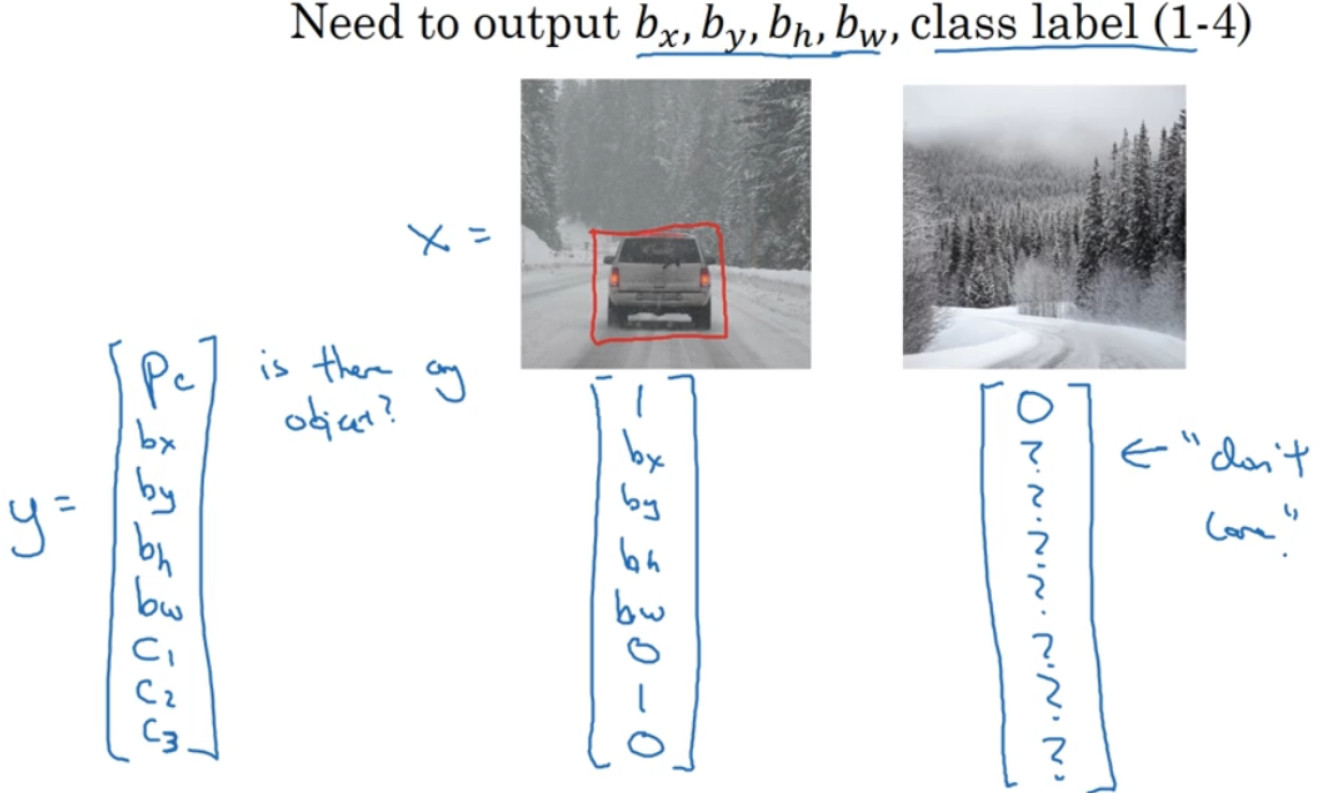
假如这是一张训练集图片，标记为x, 即上图的汽车图片。而在y当中，第一个元素${p_c} = 1$,因为图中有一辆车，${b_x}$，${b_y}$ , ${b_w}$ , ${b_h}$会指明边界框的位置，所以标签训练集需要标签的边界框。图片中是一辆车，所以结果属于分类 2，因为定位目标不是行人或摩托车，而是汽车，所以：${c_1} = 0$，${c_2} = 1$，${c_3} = 0$,如果图片中没有检测对象，这种情况下，${p_c} = 0$，y的其它参数将变得毫无意义。

神经网络的损失函数，其参数为类别y和网络输出${\hat y}$,如果采用平方误差策略，则: $L(\hat y,y) = {({{\hat y}_1} - {y_1})^2} + {({{\hat y}_2} - {y_2})^2} + ...{({{\hat y}_8} - {y_8})^2}$损失值等于每个元素相应差值的平方和。

当${y_1} = 1$时，平方误差策略可以减少这 8 个元素预测值和实际输出结果之间差值的平方。当${y_1} = 0$时，y矩阵中的后 7 个元素都不用考虑，只需要考虑神经网络评估${y_1}$(即${p_c}$)的准确度。

实际应用中，你可以对${c_1}$，${c_2}$，${c_3}$和 softmax 激活函数应用对数损失函数，并输出其中一个元素值，通常做法是对边界框坐标应用平方差或类似方法，对${p_c}$应用逻辑回归函数，甚至采用平方预测误差也是可以的。