2-4 网络中的网络以及 1×1 卷积

网络中的网络以及 1×1 卷积（ Network in Network and 1×1 convolutions）

过滤器为 1×1，这里是数字 2，输入一张 6×6×1 的图片，然后对它做卷积，起过滤器大小为 1×1×1，结果相当于把这个图片乘以数字 2，所以前三个单元格分别是 2、 4、 6 等等。用 1×1 的过滤器进行卷积，似乎用处不大，只是对输入矩阵乘以某个数字。但这仅仅是对

6×6×1 的一个通道图片来说， 1×1 卷积效果不佳。

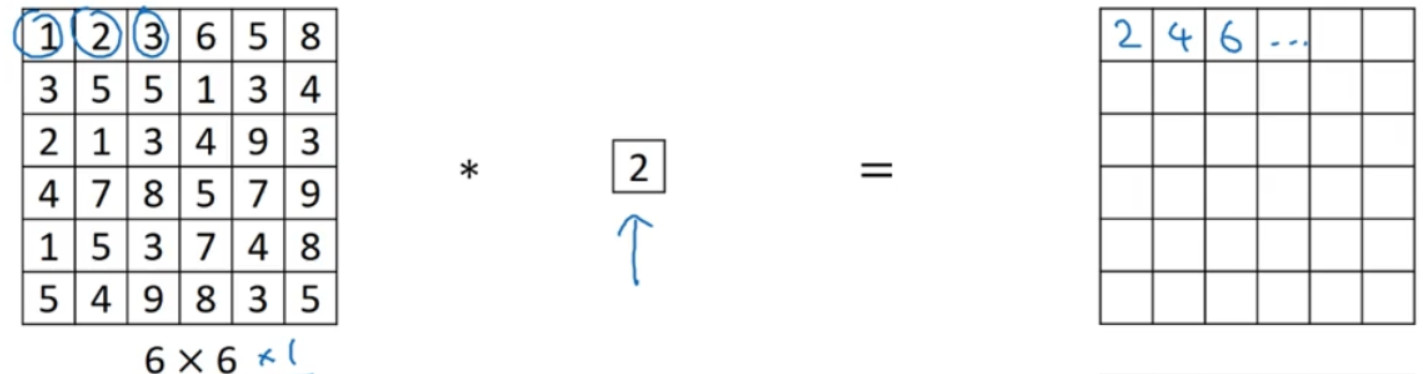
如果是一张 6×6×32 的图片，那么使用 1×1 过滤器进行卷积效果更好。具体来说， 1×1 卷积所实现的功能是遍历这 36 个单元格，计算左图中 32 个数字和过滤器中 32 个数字的元积之和，然后应用 ReLU 非线性函数。

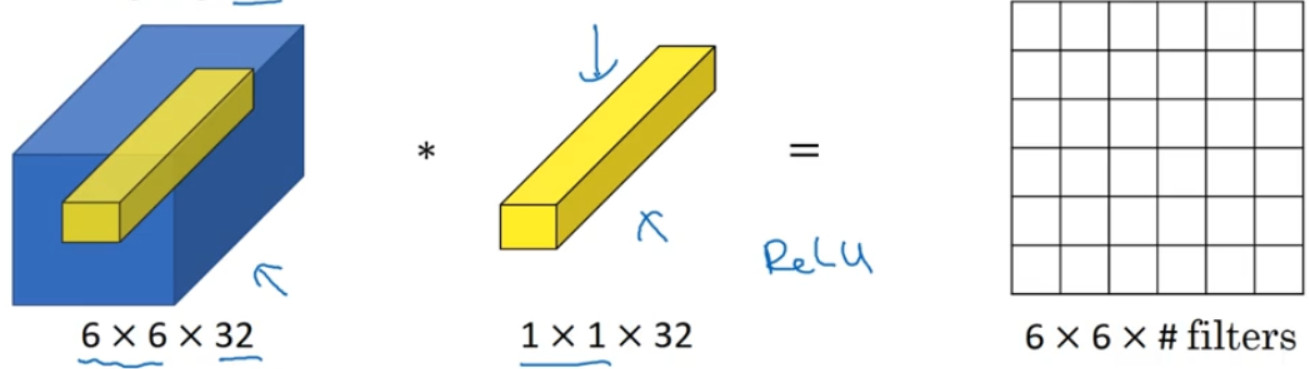
这个 1×1×32 过滤器中的 32 个数字可以这样理解，一个神经元的输入是 32 个数字，即相同高度和宽度上某一切片上的 32 个数字，这 32 个数字具有不同通道，乘以 32 个权重（将过滤器中的 32 个数理解为权重），然后应用 ReLU 非线性函数，在这里输出相应的结果。

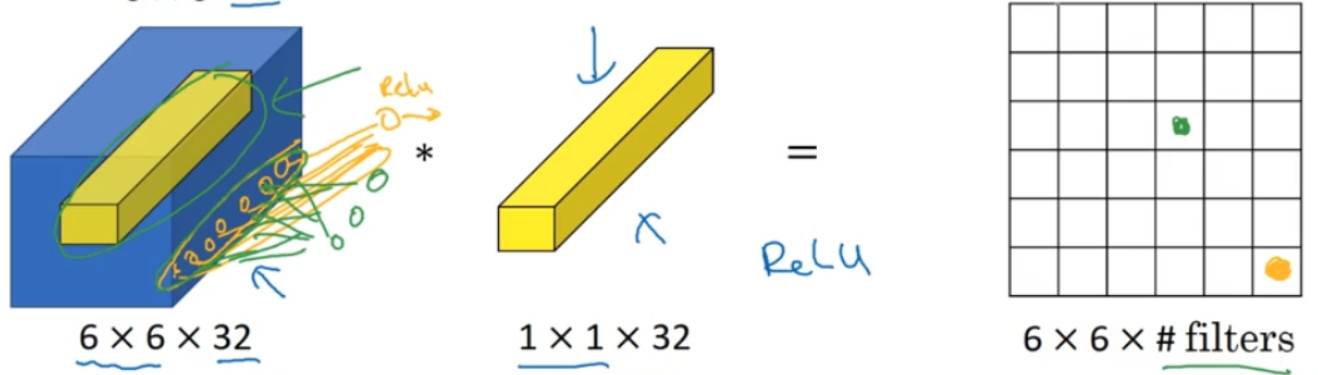
一般来说，如果过滤器不止一个，而是多个，就好像有多个输入单元，其输入内容为一个切片上所有数字，输出结果是 6×6 过滤器数量。

所以 1×1 卷积可以从根本上理解为对这 32 个不同的位置都应用一个全连接层，全连接层的作用是输入 32 个数字,输出结果是 6×6×#filters（过滤器数量），以便在输入层上实施一个非平凡（ non-trivial）计算。

这种方法通常称为 1×1 卷积，有时也被称为 Network in Network。

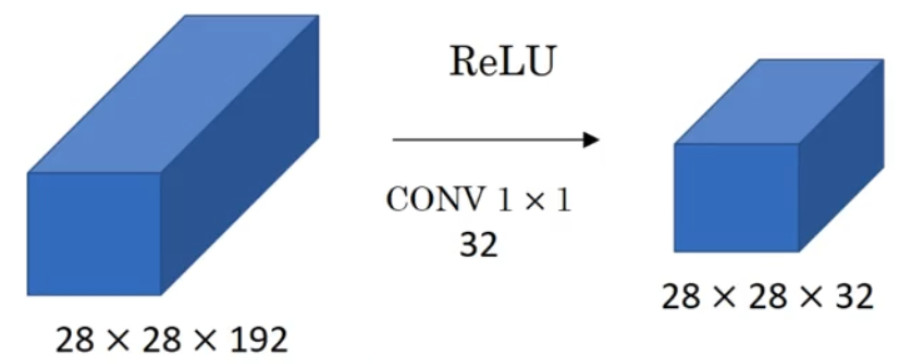
假设这是一个 28×28×192 的输入层，你可以使用池化层压缩它的高度和宽度，这个过程我们很清楚。但如果通道数量很大，该如何把它压缩为 28×28×32 维度的层呢？你可以用 32

个大小为 1×1 的过滤器，严格来讲每个过滤器大小都是 1×1×192 维，因为过滤器中通道数

必须与输入层中通道的数量保持一致。但是你使用了 32 个过滤器，输出层为 28×28×32，这就是压缩通道数的方法，对于池化层我只是压缩了这些层的高度和宽度。

当然如果你想保持通道数 192 不变，这也是可行的， 1×1 卷积只是添加了非线性函数，当然也可以让网络学习更复杂的函数，比如，我们再添加一层，其输入为 28×28×192，输出为 28×28×192。

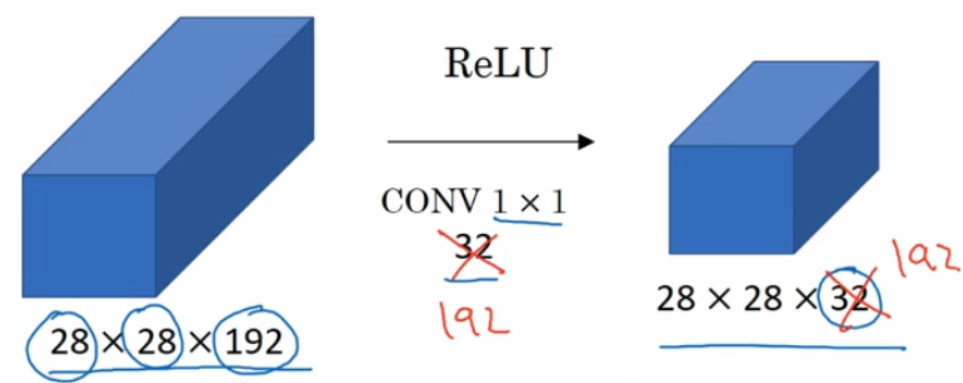
1×1 卷积层就是这样实现了一些重要功能的（doing something pretty non-trivial），它给神经网络添加了一个非线性函数，从而减少或保持输入层中的通道数量不变，当然如果你愿意，也可以增加通道数量。